Продолжение расчета фильтра Баттеруорта.

6'. Значения коэффициентов a_m и g_m (6.3.12), вычисленные по нормированным значениям s_n.

a_m = 0.067, 0.102, 0.198, 0.284, 0.317, 0.405, 0.407, 0.444.

g_m = 0.655, 1.527, 0.697, 1.436, 0.783, 1.277, 0.917, 1.091.

Коэффициент g билинейного преобразования для ненормированных значений w и полюсов s_n имеет классическую форму: g = 2/Dt. Соответственно, для нормированных значений: g = 2/(Dt·w_o). После билинейного z-преобразования выражения (6.3.11), получаем:

H(z) = G 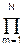G_m (1-z²)/(1-b_m z+c_m z²). (6.3.13)

G_m = 1/(g+a_m+g_mg^-1. (6.3.14)

b_m = 2G_m(g-g_mg^-1). (6.3.15)

c_m = G_m(g-a_m+g_mg^-1. (6.3.16)

Продолжение расчета фильтра Баттеруорта(по нормированным полюсам s_n).

7. Значения коэффициента g: g = 1.363.

8. Значения коэффициентов G_m по (6.3.14):

G_m = 0.523, 0.387, 0.483, 0.37, 0.444, 0.37, 0.409, 0.384.

9. Значения коэффициентов b_m по (6.3.15):

b_m = 0.924, 0.188, 0.823, 0.23, 0.7, 0.315, 0.565, 0.432.

10. Значения коэффициентов c_m по (6.3.16):

c_m = 0.93, 0.921, 0.809, 0.789, 0.719, 0.701, 0.666, 0.659.

11. Общий нормировочный множитель G: G = 1.264·10^-3.

12. Заключительная передаточная функция:

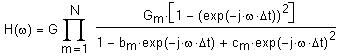
При построении графика данной функции можно убедиться, что она полностью соответствует рисунку 6.3.2.

13. Уравнение одной секции фильтра:

y_m,k = G_m·(y_m-1,k - y_m-1,k-2) + b_m y_m,k-1 – c_m y_m,k-2 .

Разные значения множителей G_m в секциях фильтра обычно опускаются и нормировкой H(z) к 1 на геометрической средней частоте фильтра определяют общий множитель G, что ускоряет вычисления:

G = 1/H(exp(-jDtw_o)). (6.3.17)

При очень малой величине порядка значения G для исключения и накопления аппаратных ошибок вычислений можно применять и другой метод: устанавливать для всех секций постоянное значение G_m = const, такое, при котором G = 1.

Если применить обратное частотное преобразование p = s(w_в-w_н)/(s²+w_в w_н), то в результате будет получен полосовой заградительный фильтр.

(!!!КР18- Разработка программы расчетов ПФ Баттеруорта по методике, аналогичной методике расчетов НЦФ).

6.4. Фильтры Чебышева /л12/.

Фильтры первого рода. Фильтры Чебышева с пульсациями передаточной функции в полосе пропускания и гладким затуханием в полосе подавления называют фильтрами Чебышева первого рода, в отличие от инверсных фильтров Чебышева (второго рода). Аппроксимационная формула фильтров Чебышева первого рода определяется выражением:

|H(W)|² = 1/ [1+d_N² T_N²(W)], (6.4.1)

где Т_N(W) - многочлен Чебышева N-го порядка:

T_n(W) = cos(n arccos(W)), W 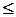1. (6.4.2)

= ch(n arcch(W)), W>1. n = 1,2,...

Критерий приближения Чебышева, который широко используется не только в теории фильтров - минимум максимальной ошибки приближения (минимаксное приближение). В соответствии с этим приближением параметры передаточной функции подбираются таким образом, чтобы в полосе передачи АЧХ наблюдались равноволновые пульсации коэффициента передачи, которые являются "платой" за повышение крутизны среза фильтра.

Полиномы Чебышева вычисляются по рекуррентной формуле:

T_n(W) = 2W T_n-1(W) - T_n-2(W), (6.4.3)

T₁(W) = W, T_o(W) = 1.

Для ФНЧ при W = w/w_p имеет место Т_n(1) = 1, |H(W)|² = 1/(1+d²) и значением d задается коэффициент пульсаций в полосе передачи. При задании полосы по уровню А_p значение d рассчитывается аналогично фильтру Баттеруорта.

Соответственно, при задании А_s на границе полосы подавления, имеем:

1/(1+d² T_N²(w_s/w_p)) = A_s². (6.4.4)

N = arcch[ 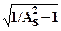/d] / arcch(w_s/w_p). (6.4.5)

Дальнейшие расчеты идентичны расчетам фильтров Баттеруорта, равно как и частотные преобразования фильтров ФНЧ в ФВЧ и ПФ.

(!!!КР16- Разработка программы расчетов фильтров Чебышева 1-го рода)

Фильтры второго рода. Для фильтров Чебышева второго рода, с гладкой передаточной характеристикой в зоне пропускания и равноволновыми пульсациями в зоне подавления, используется функция:

|H(W)|² = 1/[1+d²(T_N²(W_s)/T_N²(W_s/W))], (6.4.6)

где W = w/w_p, W_s = w_s/w_p. Условие задания параметра d остается без изменений. На границе полосы подавления при w = w_s: 1+d²T_N²(w_s/w_p) = 1/A_s², откуда значение N также определяется аналогично фильтру первого рода. Дальнейший порядок расчетов фильтров Чебышева второго рода не отличается от фильтров первого рода.

(!!!КР17- Разработка программы расчетов фильтров Чебышева 2-го рода)

6.4. Дополнительные сведения.

При использовании РЦФ очень часто упускается вопрос длительности фактического затухания переходного процесса. Между тем, для эффективного запуска РЦФ необходим поток входных данных x_n и множество начальных значений у_n. Если начальные значений у_n неизвестны и принимаются равными нулю, начальный переходной процесс включения неизбежен. При этом существует четкая тенденция - чем больше крутизна фильтра, тем дольше затухает переходной процесс. Поэтому РЦФ применяют, в основном, при обработке достаточно протяженных массивов. При обработке коротких массивов, длина которых соизмерима с длительностью переходного процесса РЦФ, необходим предварительный подбор начальных значений у_n. Проводится он, как правило, чисто эмпирически, с использованием различных наборов начальных данных.

Второй фактор, который следует учитывать - сдвиг фазы. Если при обработке данных сдвиг фазы входных сигналов недопустим, то следует применять либо дополнительный компенсирующий фильтр, восстанавливающий фазу обработанных сигналов, либо применять последовательную двойную фильтрацию однотипным рекурсивным фильтром с прямым и обратным проходом обрабатываемых данных.

(!!!КР15 - Разработка программы расчетов рекурсивных частотных фильтров с полиномами на базе экспоненциальных функций).