Пример расчета фильтра высоких частот Баттеруорта.

Техническое задание:

- Шаг дискретизации данных Dt = 0.0005 сек.

Частота Найквиста f_N = 1/2Dt = 1000 Гц, ω_N = 6.283·10³ рад.

- Граничная частота полосы пропускания: f_p = 700 Гц, w_p = 4.398·10³ рад.

- Граничная частота полосы подавления: f_s = 500 Гц, w_s = 3.142·10³ рад.

- Коэффициенты неравномерности: А_р = А_s = 0.1.

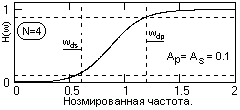Рис. 6.2.1.

Расчет дополнительных параметров:

1. d = A_p 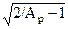/(1-A_p): d= 0.484.

2. Деформированные частоты по формуле (6.1.4):

w_dp = 7.85·10³ рад. w_ds = 4·10³ рад.

3. Порядок фильтра по формуле (6.2.8): N = 4.483.

Для расчетов принимаем N=4.

4. Частота среза фильтра по формуле (6.2.9):

w_dc = 6.549·10³ рад (1042 Гц),

5. Строим график функции H(w) = 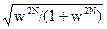, w = ω/ω_dc, (рис.6.2.1).

6. Полюса p_n фильтра полностью повторяют полюса ФНЧ (рис. 6.1.2), а, соответственно, повторяются и значения коэффициентов a_m.

7. g = 0.611, G₁ = 0.543, G₂ = 0.4, b₁ = - 0.681, b₂ = - 0.501, c₁ = 0.492, c₂ = 0.098.

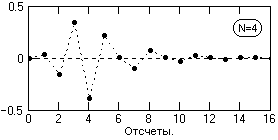Рис. 6.2.2.

При сравнении коэффициентов b_m, c_m и коэффициентов в числителе передаточных функций ФВЧ с соответствующими коэффициентами ФНЧ предыдущего примера можно заметить, что в данном фильтре относительно ФНЧ произошла только смена знаков коэффициентов при нечетных степенях z. Это объясняется тем, что заданные в данном примере параметры ФВЧ по частоте соответствуют частотному реверсу ФНЧ: w' = p-w, что приводит к частотному реверсу передаточной функции низкочастотного фильтра и превращению его в высокочастотный фильтр. Этот способ обращения ФНЧ также может использоваться для расчетов ФВЧ.

8. Импульсная реакция фильтра, вычисленная по (6.2.10) при подаче на вход фильтра импульса Кронекера приведена на рис. 6.2.2.

6.3. Полосовой фильтр Баттеруорта /л12/.

Как известно, полосовой фильтр можно получить непосредственной комбинацией низкочастотного и высокочастотного фильтра при перекрытии полосы пропускания фильтров. Аналогичный эффект достигается и частотным преобразованием ФНЧ, которое в этом случае имеет вид:

p = s+1/s. (6.3.1)

Подставив в (6.3.1) значения p = jW и s = jw, получим:

W = [w²-1]/w,

w²-Ww-1 = 0. (6.3.2)

Корни уравнения (6.3.2):

(w)_1,2 = W/2 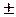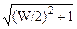. (6.3.3)

Расщепление спектра. При W=0 имеем w = 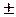1, т.е. центр полосы пропускания ФНЧ (от -W_с до +W_с) расщепляется на два (как и положено, для полосовых фильтров) и смещается в точки w = 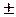1. Подставив в (6.3.3) граничную частоту W_с=1 нормированного ФНЧ, определяем граничные частоты нормированного полосового фильтра в виде пары сопряженных частот:

w₁ = 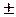0.618, w₂ = 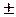1.618

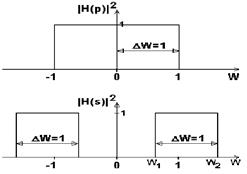Рис. 6.3.1. Расщепление полосы.

Сущность произведенного преобразования наглядно видна на рис. 6.3.1. Ширина полосы пропускания нормированного ПФ равна 1.

Полученное преобразование можно распространить на полосовой фильтр с ненормированными частотами w_н и w_в.

Введем понятие геометрической средней частоты фильтра w_о:

w_о= 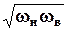. (6.3.4)

Ширина полосы пропускания ПФ связана (см. рис.6.3.1) с граничной частотой ФНЧ соотношением:

Dw = w_в-w_н = w_с = w_н.

В долях средней геометрической частоты:

W_н = (w_в-w_н)/w_о = W_с. (6.3.5)

Заменяя в (6.3.4-6.3.5) значение w_в на произвольную частоту w и подставляя в (6.3.5) значение ω_н = ω·ω_о² из (6.3.4), получаем произвольную частоту W:

W = (w-w_н)/w_о = w/w_o-w_o/w. (6.3.6)

Отсюда, в выражении (6.1.1) вместо нормированной частоты W = w/w_с можно применить функцию частоты полосового фильтра w(w):

w(w) = (w²-w_о²)/[w(w_в-w_н)],

или, подставляя (6.3.4) вместо ω_о:

w(w) = (w²-w_нw_в)/[w(w_в-w_н)]. (6.3.7)

Тем самым передаточная функция ФНЧ выражается в единицах, которые позволяют после применения преобразования (6.3.1) использовать для задания необходимые граничные частоты w_н и w_в полосового фильтра.