Продолжение примера расчета фильтра.

7. Вычисляем значения коэффициентов a_m по формуле (6.1.17):

- N=4: a₁ = 0.765, a₂ = 1.848.

- N=5: a₁ = 0.618, a₂ = 1.618.

Билинейное преобразование. Для перевода передаточной функции фильтра в z-область производится билинейное преобразование, для чего в выражение (6.1.16) подставляется параметр р:

p = g·(1-z)/(1+z). (6.1.18)

С учетом автоматического возврата к нормальной (недеформированной) шкале частот в главном частотном диапазоне z-преобразования значение коэффициента g:

g = 2/(Dt·ω_dc). (6.1.19)

После перехода в z-область и приведения уравнения передаточной функции в типовую форму, для четного N получаем передаточную функцию из М=N/2 биквадратных блоков:

H(z) = G 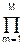G_m (1+z)² /(1-b_m z+c_m z²). (6.1.20)

G_m = 1/(g² + a_mg + 1). (6.1.21)

b_m = 2·G_m (g² - 1). (6.1.22)

c_m = G_m (g² - a_mg + 1). (6.1.23)

При любом нечетном N добавляется один постоянный линейный блок первого порядка, который можно считать нулевым блоком фильтра (m=0):

H(z) = G 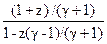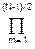G_m (1+z)² /(1-b_m z+c_m z²), (6.1.24)

при этом, естественно, в выражении (6.1.24) используются значения коэффициентов G_m, b_m и c_m, вычисленные по (6.1.21-6.1.23) для данного нечетного значения N.

При z=exp(-jw) главный диапазон функций H(z) от -p до p. Для получения передаточной функции в шкале физических частот достаточно вместо z в выражения (6.1.20, 6.1.24) подставить значение z=exp(-jwDt), где Dt – физический интервал дискретизации данных, и проверить соответствие расчетной передаточной функции заданным условиям.

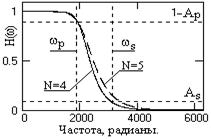Рис. 6.1.3. 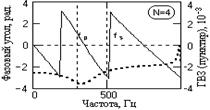Рис. 6.1.4.