Тема 4: НЕРЕКУРСИВНЫЕ ЧАСТОТНЫЕ ФИЛЬТРЫ.

Недостаточно овладеть премудростью, нужно уметь пользоваться ею.

Цицерон. О высшем благе и высшем зле.

(Римский сенатор и философ)

Мало пользы от теории бокса, пока сам не научишься махать кулаками.

Евгений Буцко. Назидания идиотам.

(Ленинградский инженер и геофизик)

Содержание: 4.1. Общие сведения. Типы фильтров. Методика расчетов. 4.2. Идеальные частотные фильтры. Импульсная реакция фильтров. 4.3. Конечные приближения идеальных фильтров. Применение весовых функций. Весовая функция Кайзера. 4.4. Дифференцирующие цифровые фильтры. 4.4. Гладкие частотные фильтры. Литература.

4.1. Общие сведения.

К наиболее известным типам нерекурсивных цифровых фильтров (НЦФ) относятся частотные фильтры, алгоритм которых для симметричных НЦФ, не изменяющих фазу сигналов, имеет вид:

y_k = 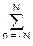h_n s_k-n .

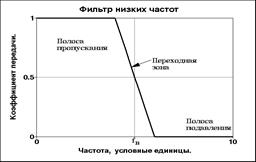
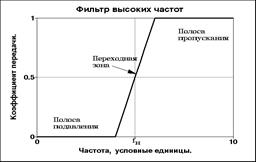
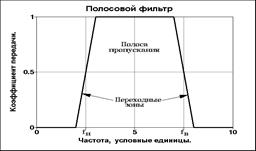Рис. 4.1.1. Типы частотных фильтров.

Типы фильтров. Выделяют три основных группы частотных фильтров: ФНЧ - фильтры низких частот (пропускание низких, подавление высоких частот во входном сигнале), ФВЧ - фильтры высоких частот (пропускание высоких, подавление низких частот) и ПФ - полосовые фильтры (пропускание определенных частот с подавлением остальных частот сигнала). Среди последних в отдельную группу иногда выделяют РФ - режекторные фильтры, понимая под ними фильтры с подавлением определенных частот (узкой полосы частот) во входном сигнале, и СФ – селекторные фильтры, обратные РФ. Схематические частотные характеристики фильтров приведены на рисунке 4.1.1. Между частотными интервалами пропускания и подавления сигнала существует зона, которая называется переходной.

Практика проектирования нерекурсивных цифровых фильтров базируется, в основном, на синтезе фильтров низких частот. Все другие виды фильтров могут быть получены из фильтров низких частот соответствующим преобразованием. Так, например, фильтр высоких частот может быть получен инверсией фильтра низких частот - вычислением разности между исходным сигналом и результатом его фильтрации низкочастотным НЦФ:

y(k) = s(k) – 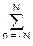h(n) s(k-n).

Отсюда, условие инверсии симметричного низкочастотного фильтра в высокочастотный:

h_в(0) = 1- h_н(0), h_в(n) = -h_н(n) при n 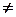0. (4.1.1)

Применяется также способ получения фильтров высоких частот из низкочастотных фильтров путем реверса частоты в передаточной функции низкочастотного фильтра, т.е. заменой переменной w на переменную w' = p-w (при Dt = 1). Для симметричных фильтров, содержащих в передаточной функции только косинусные члены аргумента w, в результате такой операции будем иметь:

cos n(p-w) = cos np cos nw = (-1)ⁿ cos nw.

Последнее означает смену знака всех нечетных гармоник передаточной характеристики фильтра и, соответственно, всех нечетных членов фильтра.

Полосовой фильтр может реализоваться последовательным применением ФНЧ и ФВЧ с соответствующим перекрытием частот пропускания. В математическом представлении это означает последовательную свертку массива данных с массивами коэффициентов h_н - низкочастотного, и h_в - высокочастотного фильтров:

v_k = h_н(n) _* s(k-n), y_k = h_в(n) _* v_k = h_н(n) _* h_в(n) _* s(k-n).

Так как операция свертки коммутативна, то вместо отдельных массивов коэффициентов ФНЧ и ФВЧ их сверткой может быть определен непосредственно массив коэффициентов полосового фильтра: h_n = h_н(n) _* h_в(n).

Полосовой режекторный фильтр также может быть получен методом инверсии полосового фильтра. Одночастотные режекторные фильтры обычно выполняются на основе простых рекурсивных цифровых фильтров, более эффективных для данных целей.

Методика расчетов НЦФ в самом общем виде включает:

1. Задание идеальной частотной передаточной функции фильтра.

2. Расчет функции отклика идеального фильтра (обратное преобразование Фурье передаточной функции фильтра).

3. Ограничение функции отклика до определенного количества членов, при этом на передаточной характеристике фильтра возникает явление Гиббса.

4. Для нейтрализации явления Гиббса производится выбор весовой функции и расчет ее коэффициентов, на которые умножаются коэффициенты функции отклика фильтра. Результатом данной операции являются значения коэффициентов оператора фильтра (импульсный отклик фильтра). По существу, операции 3 и 4 представляют собой усечение ряда Фурье динамического (временного) представления передаточной функции фильтра определенной весовой функцией.

5. С использованием полученных значений коэффициентов оператора фильтра производится построение его частотной характеристики и проверяется ее соответствие поставленной задаче.

4.2. Идеальные частотные фильтры.

Идеальным полосовым фильтром называется фильтр, имеющий единичную амплитудно-частотную характеристику в полосе от определенной нижней частоты w_н до определенной верхней частоты w_в и нулевой коэффициент передачи за пределами этой полосы (для цифровых фильтров - в главном частотном диапазоне).

Импульсная реакция фильтра (коэффициенты оператора) находится преобразованием Фурье заданной передаточной функции H(w). В общем случае:

h(nDt) = (1/2p) 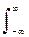H(w) exp(jwnDt) dw.

Для получения вещественной функции импульсного отклика фильтра действительная часть передаточной функции должна быть четной, а мнимая - нечетной. Цифровые фильтры задаются в главном частотном диапазоне, границы которого (частота Найквиста 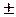w_N) определяются интервалом дискретизации данных (w_N = p/Dt), подлежащих фильтрации, и соответственно определяют интервал дискретизации оператора фильтра (Dt = p/w_N). Для фильтров с нулевым фазовым сдвигом мнимая часть передаточной функции должна быть равна нулю, при этом оператор фильтра определяется косинусным преобразованием Фурье:

h(nDt)= (1/p) 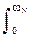H(w) cos(npw/w_N) dw, n = 0,1,2,... (4.2.1)

Для идеального полосового фильтра H(w)=1 в полосе частот от w_н до w_в и интеграл (4.2.1) вычисляется в этих пределах. Идеальные фильтры низких и высоких частот можно считать частными случаями идеальных полосовых фильтров с полосой пропускания от 0 до w_в для низкочастотного и от w_н до w_N для высокочастотного фильтра.

При интервале дискретизации данных Dt, условно принимаемым за 1, главный частотный диапазон передаточных функций ограничивается значением частоты Найквиста от -p до p. Если на практике интервал дискретизации данных в физических единицах отличается от 1, то это сказывается только на изменении масштаба частотной шкалы передаточных функций.

Пример 1. Dt = 0.1 сек. f_N = 1/2Dt = 5 Гц. w_N = p/Dt = 10 p.

Пример 2. Dx = 10 метров. f_N = 0.05 м^-1. w_N= 0.1 p.

Во всех дальнейших выражениях значение Dt, если это специально не оговорено, будем принимать равным 1.

При H(w)=A=1 в полосе пропускания w_н-w_в, и H(w)=0 за ее пределами, для идеальных симметричных полосовых НЦФ из (4.2.1) в общем виде получаем:

h(n) = (А/p) [w_в sinc(nw_в) - w_н sinc(nw_н)], (4.2.2)

h_o = (w_в - w_н)/p, h(n) = (sin nw_в - sin nw_н)/(np).

где sinc(nw) = sin(nw)/(nw) - функция интегрального синуса (функция отсчетов), бесконечная по координате w.

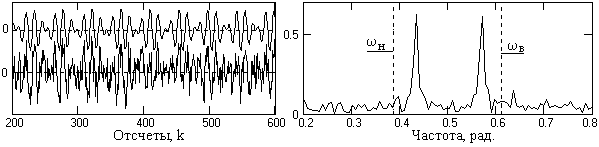Рис. 4.2.1. Входные сигналы. Рис. 4.2.2. Спектр сигнала и границы фильтра.

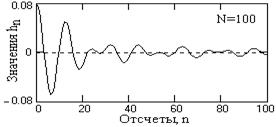Рис. 4.2.3. Оператор фильтра.

На рис. 4.2.1 приведен пример сигнала однотональной балансной амплитудной модуляции (чистого – вверху, и с наложенными шумами внизу, мощность шумов равна мощности сигнала). Если информация заключена в частоте и амплитуде модулирующего сигнала, то полосовой фильтр выделения сигнала из шумов, спектр которого для одной модулирующей частоты приведен на рис. 4.2.2, в идеальном случае должен иметь плоскую частотную характеристику в границах возможных вариаций модулирующей частоты (от w_н до w_в).

На рис. 4.2.3 приведен оператор полосового фильтра, вычисленный по (4.2.2) для приведенных выше условий с ограничением по n до N=100. Как видно из рисунка, оператор затухает достаточно медленно и явно усечен, что должно сказаться на форме частотной характеристики фильтра. Все дальнейшие вычисления будут проводиться на продолжении данного примера.

4.3. Конечные приближения идеальных фильтров /л24/.

Оператор идеального частотного НЦФ, как это следует из выражения (4.2.2), представляет собой бесконечную затухающую числовую последовательность, реализующую заданную передаточную функцию:

H(w) = 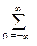h(n) cos nw. (4.3.1)

На практике бесконечный ряд (4.3.1) всегда приходится ограничивать определенным числом членов его конечного приближения

H'(w) = 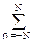h(n) cos nw,

при этом передаточная функция осложняется явлением Гиббса и появляется переходная зона между полосами пропускания и подавления сигнала (рис. 4.3.1, пунктирная кривая при N=100). Явление Гиббса формирует первые выбросы передаточной функции на расстоянии p/(2(N+1)) от скачков (разрывов первого рода). Если ширину переходной зоны D_p в первом приближении принять по расстоянию между первыми выбросами по обе стороны от скачка функции H(w), то ее значение будет ориентировочно равно p/(N+1) = D_p.

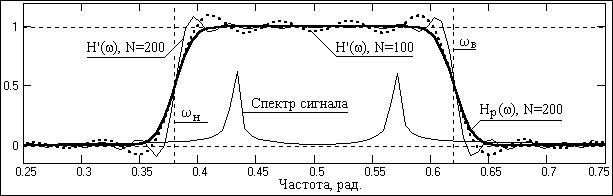Рис. 4.3.1. Передаточные функции полосового фильтра.

Применение весовых функций. Если уровень пульсаций передаточной функции, определяемый явлением Гиббса, не удовлетворяет поставленным задачам фильтрации данных, рекомендуется использование сглаживающих весовых функций. С учетом того, что при применении весовых функций происходит расширение переходных зон примерно в два раза, значение ширины переходной зоны будет равным D_p = 2p/N. Отсюда можно определить минимальное число членов усеченного ряда:

N = 2p/D_p. (4.3.2)

Для примера на рис. 4.3.1 значение N принято равным 200, при этом крутизна переходной зоны увеличилась (тонкая кривая H'(w), N=200), создавая запас на последующее сглаживание весовой функцией.

Выбор весовых функций целесообразно осуществлять по допустимой величине осцилляций усиления сигнала в полосе подавления, т.е. по относительному значению амплитуды первого выброса на передаточных характеристиках весовых функций. Для выбранной весовой функции (с учетом числа ее членов по (4.3.2)) производится расчет весовых коэффициентов p_n, после чего устанавливаются окончательные значения оператора фильтра:

h_n = h(n)·p_n. (4.3.3)

Подстановкой коэффициентов (4.3.3) в (4.3.1) рекомендуется произвести построение полученной передаточной характеристики фильтра и непосредственно по ней оценить пригодность фильтра для поставленных задач. Это наглядно видно на рис. 4.3.1, где для нашего примера была применена весовая функция Гаусса. Передаточная функция H_p(w) имеет практически такую же крутизну, как и функция H'(w) при N=100 и практически плоскую вершину в интервале спектра сигнала. Качество работы фильтра для сигнала, приведенного на рис. 4.2.1, можно видеть на рис. 4.3.2.

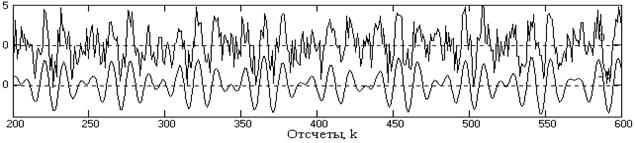Рис. 4.3.2. Полосовая фильтрация (вверху – входной сигнал, внизу – выходной).

Весовая функция Кайзера. Наибольшее распространение при расчетах частотных НЦФ получила весовая функция Кайзера:

p(n) = .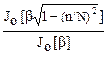

Это объясняется тем, что параметры функции Кайзера могут устанавливаться непосредственно по техническим требованиям к передаточным функциям проектируемых фильтров – допустимой ширине переходной зоны D_p и значению коэффициента шума фильтра d (максимальным значениям осцилляций передаточной функции в единицах коэффициента передачи в полосе пропускания).

Кайзером установлено, что для заданного значения d произведение количества членов оператора НЦФ на ширину переходной зоны является величиной постоянной. Оно получило название D-фактора:

D = N·D_p/p.

С другой стороны, установлены следующие эмпирические соотношения между D-фактором и параметром b функции Кайзера:

D = (А-7.95)/14.36 при А>21.

= 0.9222 при А<21.

b = 0.1102(A-8.7) при А>50.

= 0 при А<21.

= 0.5842(A-21)^0.4 + 0.07886(A-21), 21<А<50.

где: А = -20 log d - затухание в децибелах.

Приведенные выражения позволяют по заданному значению коэффициента шума d определить параметр b функции Кайзера, а через D-фактор число членов фильтра:

N = pD/D_p.

При проектировании полосовых фильтров проверка передаточной функции полученного оператора НЦФ исходному заданию по значению коэффициента шума является обязательной. Это объясняется тем, что поскольку полоса пропускания полосового фильтра ограничена двумя скачками, на передаточной характеристике возникают два центра осцилляций, при этом наложение осцилляций может как уменьшить, так и увеличить амплитуду суммарных осцилляций. Если за счет наложения произойдет увеличение амплитуды осцилляций, то расчет НЦФ следует повторить с уменьшением исходного значения d.