Пример расчета полосового фильтра.

Произвести расчет ПФ при следующих исходных параметрах: w_н = 0.3p, w_в = 0.6p, D_p = 0.1p, d= 0.02.

1. А= -20 log d. А= 34. 2. N= p (A-7.95)/(14.36 D_p). N= 18.

3. b= 0.5842(A-21)^0.4 +0.07886(A-21). b= 2.62. 4. h_о= (w_в-w_н)/p. h_о= 0.3

5. h(n)= (sin nw_в-sin nw_н)/(np). h(n)= 0.04521, -0.24490, -0.09515,...., 0.02721.

6. p_n= J_o{b } / J_o{b}. p_n = 1.00, 0.997, 0.9882, .......

7. Oператор фильтра: h_n= h(n)p_n, n=0,1,2,...,N. h_-n=h_n. h_n= 0.3000, 0.04508, -0.2420, ........

8. Проверка по формуле: H(w) = 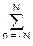h_n cos nw, 0 £ w £ p.

Для оценки формы передаточной функции количество точек спектра в интервале 0-p достаточно задать равным 2N, т.е. с шагом Dw £ p/36.

(!!!КР7 - Разработка программы расчета сглаживающих НЦФ).

(!!!КР8 - Разработка программы расчета полосовых НЦФ).

4.4. Дифференцирующие цифровые фильтры.

Передаточная функция. Из выражения для производной

d(exp(jwt))/dt = jw exp(jwt)

следует, что при расчете фильтра производной массива данных необходимо аппроксимировать рядом Фурье передаточную функцию вида H(w) = jw. Поскольку коэффициенты такого фильтра будут обладать нечетной симметрией (h_-n = -h_n) и выполняется равенство

h_n [exp(jwn)-exp(-jwn)] = 2j h_n sin nw,

то передаточная характеристика фильтра имеет вид:

H(w) = 2j(h₁ sin w + h₂ sin 2w + ... + h_N sin Nw),

т.е. является мнимой нечетной, a сам фильтр является линейной комбинацией разностей симметрично расположенных относительно s_k значений функции. Уравнение фильтрации:

y_n = 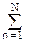h_n(s_k+n - s_k-n).

Если дифференцированию подлежит низкочастотный сигнал, а высокие частоты в массиве данных представлены помехами, то для аппроксимации в пределах частотного диапазона 0-w_N задается передаточная функция фильтра вида:

H_н(w) = w, w £ w_в, H_н(w) = 0, w_в< w £ w_N.

Оператор дифференцирующего фильтра:

h(n) = (1/p) 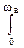H_н(w) sin(npw/w_N) dw, n = 0,1,2,... (4.4.1)

Принимая, как обычно, w_N = p (Dt = 1) и решая (4.4.1) при H_н(w) = w, получаем:

h_n = (1/p)[sin(nw_в)/n² - w_в cos(nw_в)/n], (4.4.2)

h_о = 0, h_-n = -h_n.

Проверка: H_н(w) = 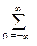h_n sin nw = 2 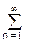h_n sin nw . (4.4.3)

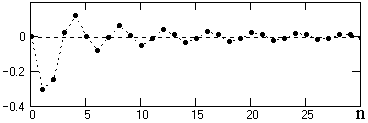Рис. 4.4.1. Коэффициенты оператора фильтра.

На рис. 4.4.1 приведен пример расчета коэффициентов дифференцирующего фильтра на интервал {0-0.5}p при Dt=1 (w_в = p/2). Операторы дифференцирующих фильтров, как правило, затухают очень медленно и, соответственно, достаточно точная реализация функции (4.4.3) весьма затруднительна.

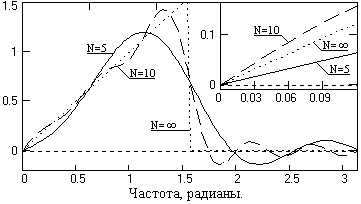Рис. 4.4.2. Частотные функции фильтров.

Ряд (4.4.3) усекается до N членов и с помощью весовых функций производится нейтрализация явления Гиббса. Явление Гиббса для дифференцирующих фильтров имеет весьма существенное значение и может приводить к большим погрешностям при обработке информации, если не произвести его нейтрализацию. Примеры ограничения оператора, приведенного на рис. 4.4.1, и соответствующие передаточные функции H_н'(w) усеченных операторов показаны на рис. 4.4.2.

Для оценки возможных погрешностей дифференцирования усеченными операторами произведем расчет фильтра при w_в = p/2. По формулам (4.4.2) определяем:

h_0-10 = 0, 0.3183, 0.25, -0.0354, -0.125, 0.0127, 0.0833, -0.0065, -0.0625, 0.0039, 0.05.

Произведем проверку работы фильтра на простом массиве данных s_n = n, производная которого постоянна и равна 1. Для массива с постоянной производной фильтр может быть проверен в любой точке массива, в том числе и в точке n=0, для которой имеем:

у = 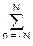h_n s_o-n = 2 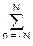n h_n,

при этом получаем: у=0.5512 при N=5, у=1.53 при N=10.

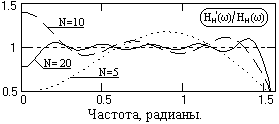Рис. 4.4.3. Погрешность дифференцирования.

Такое существенное расхождение с действительным значением производной объясняется тем, что при w=0 тангенс угла наклона реальных передаточных функций фильтра, как это видно на рисунке 4.4.2, весьма существенно отличается от тангенса угла наклона аппроксимируемой функции H(w)= w. На рис. 4.4.3 приведены частотные графики относительной погрешности дифференцирования s = H_н'(w)/H_н(w) с вычислением значений на нулевой частоте по пределам функций при N ® ¥. На рис. 4.4.4 приведен пример операции дифференцирования s_*h гармоники s с частотой w_o оператором с N=10 в сопоставлении с точным дифференцированием ds/dk.

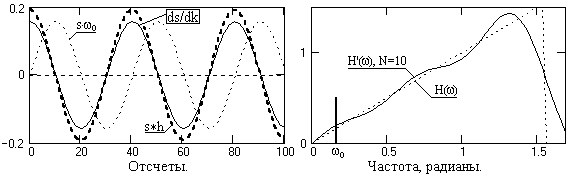Рис. 4.4.4. Пример операции дифференцирования.

Применим для нейтрализации явления Гиббса весовую функцию Хемминга. Результат нейтрализации для фильтра с N=10 приведен на рис. 4.4.5. Повторим проверочный расчет дифференцирования на массиве s_n = n и получим результат у=1.041, т.е. погрешность дифференцирования уменьшается порядок.

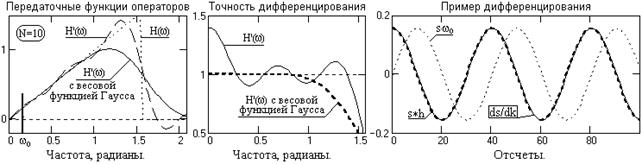Рис. 4.4.5. Дифференцирование с применением весовой функции.

Аналогично производится расчет и полосовых дифференцирующих фильтров с соответствующим изменением пределов интегрирования в (4.4.1) от w_н до w_в. При этом получаем:

h_n = (w_нcos nw_н-w_вcos nw_в)/(np) + (sin nw_в-sin nw_н)/(n2p).

(!!!КР9- Разработка программы расчета НЦФ дифференцирования)

(!!!КР10- Оценка возможностей усечения операторов НЦФ, умноженных на весовые функции).

4.5. Гладкие частотные фильтры /л24/.

В некоторых случаях (при последовательном соединении фильтров, при выделении сигналов на уровне сильных помех и т.п.) осцилляции на передаточных характеристиках фильтров являются весьма нежелательными даже при их малой остаточной величине.

Принцип синтеза фильтров. Очевидно, что фильтры с гладкой передаточной характеристикой можно получить только в том случае, если возможно разложение передаточной функции в конечный ряд Фурье.

Допустим, мы имеем симметричный НЦФ с передаточной функцией:

H(w) = h_о+ 2 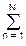h_n cos nw. (4.5.1)

Как известно, cos nw равен полиному по cos w степени n, при этом выражение (4.5.1) можно записать в виде:

H(w) = 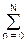g_n (cos w)ⁿ = 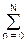g_n xⁿ, (4.5.2)

где переменная х=cos w изменяется от -1 до 1 (поскольку w изменяется от 0 до p). Преобразование переменной представляет собой нелинейное растяжение оси абсцисс с поворотом на 180^o (по переменной х передаточные функции ФНЧ похожи на ФВЧ и наоборот) с выражением функции через степенной полином. Последнее примечательно тем, что синтез гладких функций на базе степенных полиномов затруднений не представляет.

Так, например, для конструирования ФНЧ в качестве исходной может быть принята степенная функция вида:

g(x)= (1+x)^z (1-x)^r, (4.5.3)

где z и r - параметры.

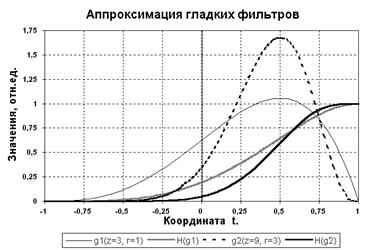Рис. 4.5.1. Примеры синтеза гладких фильтров.

Функция (4.5.3) имеет нули порядка z и r в точках соответственно х = -1 и х = 1 (рис. 4.5.1), причем значения z и r характеризуют степень касания функцией оси абсцисс (чем больше порядок, тем медленнее функция "отрывается" от оси абсцисс).

Если функцию (4.5.3) проинтегрировать в пределах от -1 до х и пронормировать на значение интеграла от -1 до 1 , то будет получена гладкая передаточная характеристика низкочастотного фильтра (рисунке 4.5.1):

H(x)= 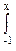g(x)dx / 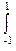g(x)dx. (4.5.4)

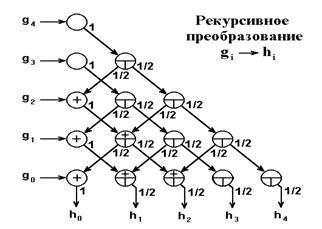Рис. 4.5.2. Схема возврата к ряду Фурье.

Функция H(x) имеет перегиб в точке (z-r)/(z+r) и переходную зону, крутизна которой тем больше, чем больше значения z и r. Подстановкой x=cos w осуществляется возврат к частотной переменной с сохранением монотонности функции.

В заключение, для определения коэффициентов фильтра h_n требуется осуществить обратное преобразование от степенной формы (4.5.2) к ряду Фурье (4.5.1). Выполнение данной операции достаточно просто производится рекурсивным способом, показанным на рис. 4.5.2. Подробное обоснование рекурсии приведено в /л24/.