Разностные операторы /л24/.
Рассмотрим примеры частотного подхода при анализе разностных операторов.
Разностный оператор 1-го порядка имеет вид:
Dsk = sk+1-sk.
Последовательное n-кратное применение оператора записывается в виде оператора n-го порядка:
Dn(sk) = D[Dn-1(sk)] = Dsk*Dn-1(sk) (2.2.1)
| k | sk | D(sk) | D2(sk) | D3(sk) | D4(sk) | D5(sk) | D6(sk) |
| -7 -6 -5 -4 -3 -2 -1 | -1 | -2 | -3 -1 | -4 -4 | -5 -10 -1 | -6 -20 -6 | |
| Кq |
Слева приводится таблица выходных значений импульсной реакции разностных операторов на единичный импульсный сигнал Кронекера. Как видно из таблицы, ряды последовательных разностей содержат знакопеременные биномиальные коэффициенты. В представленной форме разностные операторы являются каузальными фазосдвигающими (односторонними), но нетрудно заметить, что операторы четных степеней могут быть переведены в симметричную форму сдвигом вперед на половину окна оператора.
В последней строке таблицы приводятся коэффициенты усиления дисперсии шумов, значение которых резко нарастает по мере увеличения порядка оператора. Это позволяет использовать разностные операторы с порядком выше 1 для определения местоположения статистически распределенных шумов в массивах данных. Особенно наглядно эту возможность можно видеть на частотных характеристиках операторов.
Подставляя сигнал s(k) = exp(jwk) в (2.2.1) и упрощая, получаем:
Dns(k) = (jn) exp(jwn/2) [2 sin(w/2)]n exp(jwk). (2.2.2)
Так как первые два множителя в выражении (2.2.2) равны 1, зависимость коэффициента передачи разностного оператора от частоты определяется вторым сомножителем (2 sin(w/2))n и представлена на рисунке 2.2.1.
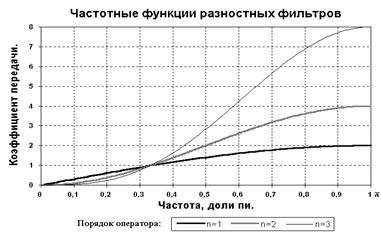 Рис. 2.2.1. Разностные фильтры.
Рис. 2.2.1. Разностные фильтры.
|
Как следует из рисунка, разностные операторы подавляют постоянную составляющую сигнала и его гармоники в первой трети интервала Найквиста и увеличивают высокочастотные составляющие сигнала в остальной части интервала тем больше, чем больше порядок оператора. Как правило, эту часть главного интервала спектра сигналов занимают высокочастотные статистические шумы.
Шумы при анализе данных также могут представлять собой определенную информацию, например, по стабильности условий измерений и по влиянию на измерения внешних дестабилизирующих факторов. На рис. 2.2.2 приведен пример выделения интервалов интенсивных шумов в данных акустического каротажа, что может свидетельствовать о сильной трещиноватости пород на этих интервалах. Такая информация относится уже не шумовой, а к весьма полезной информации при поисках и разведке нефти, газа и воды.
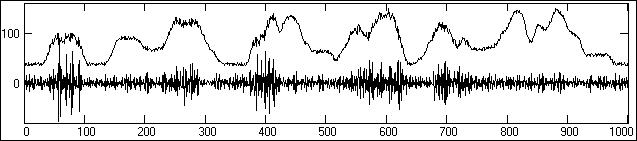
Рис. 2.2.2.
Восстановление данных. Разностные операторы имеют одну особенность: оператор n+1 порядка аннулирует полином степени n, т.е. свертка оператора n+1 порядка с полиномом n-ой степени дает нулевые значения: Dn+1 * Pn(k) = 0. Эту особенность можно использовать для создания очень простых и достаточно надежных операторов восстановления в массивах пропущенных и утраченных значений или для замены аннулированных при обработке величин (например, явных выбросов).
Пример.P2(k) = xk = 1+2k-k2, k = 0,1,2,... xk = 1,2,1,-2,-7,-14,-23,-34,... yk = xk*D3=0,0,0,0,...
Если считать, что отрезок данных, содержащий пропуск, является многочленом некоторой степени, то свертка данных с разностным оператором следующего порядка должна быть равна нулю. Так, при аппроксимации данных многочленом третьей степени для любой точки массива должно выполняться равенство:
D4·(sk) = sk-2-4sk-1+6sk-4sk+1+sk+2 = 0.
Интерполяционный фильтр восстановления утраченной центральной точки данных:
sk = (-sk-2+4sk-1+4sk+1-sk+2)/6. (2.2.3)
Соответственно, оператор фильтра восстановления данных h(n) = (-1,4,0,4,-1)/6. Коэффициент усиления шумов s2 = 17/18 = 0.944.
Пример.Фактический отрезок массива данных: xk = {3,6,8,8,7,5,3,1}.
Допустим, что на отрезке был зарегистрирован явный выброс: xk = {3,6,8,208,7,5,3,1}.
Отсчет с выбросом аннулирован. Замена отсчета: x3 = (-x1+4x2+4x4-x5)/6= (-6+32+28-5)/6 » 8.17.
В массиве утрачен 5-й отсчет. Восстановление: x4 = (-x2+4x3+4x5-x6)/6 = (-8+32+20-3)/6 » 6.83.
Принимая в (2.2.3) k = 0 и подставляя сигнал sk = exp(jwk), получаем частотную характеристику, в данном случае - интерполяционного фильтра 4-го порядка:
H(w) = (4 cos w - cos 2w)/3.
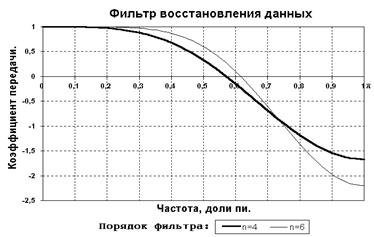 Рис. 2.2.3. Разностные фильтры.
Рис. 2.2.3. Разностные фильтры.
|
Вид частотной характеристики для фильтров восстановления пропущенных данных 4-го и 6-го порядков приведен на рис. 2.2.3. Графики наглядно показывают, что применение разностных интерполяционных фильтров восстановления данных возможно только для сигналов, высокочастотные и шумовые составляющие которых минимум в три раза меньше частоты Найквиста. Интерполяционные фильтры выше 4-го порядка применять не рекомендуется, т.к. они имеют коэффициент усиления шумов более 1.
На рис. 2.2.4 – 2.2.6 приведены примеры восстановления утраченных данных во входных сигналах оператором 3-го порядка и спектры сигналов в сопоставлении с передаточной функцией оператора восстановления данных. В сигналах утрачен каждый 10-ый отсчет (например, при передаче данных) при сохранении тактовой частоты нумерации данных. Учитывая, что все значения входных сигналов положительны, индикатором пропуска данных для работы оператора служат нулевые значения. В любых других случаях для оператора восстановления данных необходимо предусматривать специальный маркер (например, заменять аннулированные данные или выбросы определенным большим или малым значением за пределами значений отсчетов).
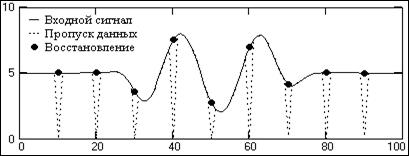
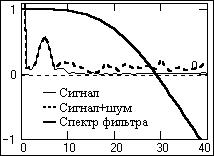
Рис. 2.2.4. Восстановление незашумленных данных. Рис.2.2.5. Спектры.
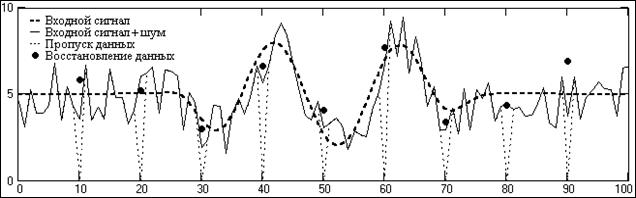
Рис. 2.2.6. Восстановление зашумленных данных.
Как следует из рис. 2.2.5, спектр полезного сигнала полностью находится в зоне единичного коэффициента частотной характеристики оператора и восстановление данных выполняется практически без погрешности (рис. 2.2.4). При наложении на сигнал статистически распределенных шумов (рис. 2.2.6) погрешность восстановления данных увеличивается, но для информационной части полного сигнала она, как и во входных данных, она не превышает среднеквадратического значения (стандарта) флюктуаций шума. Об этом свидетельствует рис. 2.2.7, полученный для сигналов на рис. 2.2.6 по данным математического моделирования при разных значениях стандарта шума (выборки по 10 точкам восстановления).
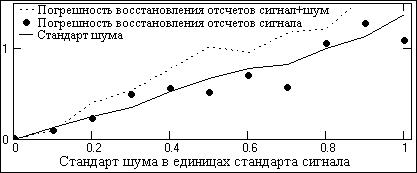
Рис. 2.2.7. Погрешности восстановления сигналов.
Аппроксимация производных - вторая большая область применения разностных операторов. Оценки первой, второй и третьей производной можно производить по простейшим формулам дифференцирования:
(sn)' = (sn+1-sn-1)/2Dt. h1 = {0.5, 0, -0.5}. (2.2.4)
(sn)'' = (sn+1-2sn+sn-1)/Dt. h2 = {1, -2, 1}.
(sn)''' = (-sn+2+sn+1-sn-1+sn-2)/2Dt. h3 = {-0.5, 0.5, 0, -0.5, 0.5}.
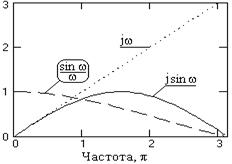 Рис. 2.2.8.
Рис. 2.2.8.
|
Оператор первой производной является нечетной функцией и имеет мнимый спектр. Если принять s(t) = exp(jwt), то истинное значение первой производной должно быть равно: s'(t) = jw exp(jwt). Передаточная функция H(w) = jw. Оценка первой производной в точке n = 0 по разностному оператору при Dt = 1: s'(0) = (exp(jw)-exp(-jw))/2 = j sin w = H1(w). Отношение расчетного значения к истинному на той же точке: K1(w) = sin(w)/w. Графики функций в правой половине главного диапазона приведены на рис. 2.2.8.
Как следует из приведенных выражений и графиков, значение К(w) равно 1 только на частоте w = 0. На всех других частотах в интервале Найквиста формула дает заниженные значения производных. Однако при обработке практических данных последний фактор может играть и положительную роль, если сигнал низкочастотный (не более 1/3 главного диапазона) и зарегистрирован на уровне высокочастотных шумов. Любое дифференцирование поднимает в спектре сигнала долю его высокочастотных составляющих. Коэффициент усиления дисперсии шумов разностным оператором дифференцирования непосредственно по его спектру в главном диапазоне:
Kq = (1/p) 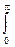 (sin w)2 dw = 0.5
(sin w)2 dw = 0.5
При точном дифференцировании по всему главному диапазону:
Kq = (1/p) 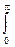 w2 dw = 3.29
w2 dw = 3.29
Следовательно, разностный оператор имеет практически в шесть раз меньший коэффициент усиления дисперсии шумов, чем полный по главному диапазону точный оператор дифференцирования.
На рис. 2.2.9 показан пример дифференцирования гармоники с частотой 0.1 частоты Найквиста (показана пунктиром) и этой же гармоники с наложенными шумами (сплошная тонкая кривая).
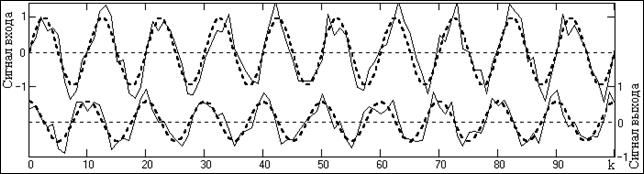
Рис. 2.2.9. Пример дифференцирования (входные сигналы – вверху, выходные – внизу).
 Рис. 2.2.10. Частотные функции 2-ой производной.
Рис. 2.2.10. Частотные функции 2-ой производной.
|
Оператор второй производной относится к типу четных функций. Частотная функция оператора: H2(w) = -2(1-cos w). Собственное значение операции H(w) = -w2. Отношение фактического значения к собственному
K2(w) = [sin(w/2)/(w/2)]2
и также равно 1 только на частоте w = 0. На всех других частотах в интервале Найквиста формула дает заниженные значения производных, хотя и меньшие по относительным значениям, чем оператор первой производной. Частотные графики функций приведены на рис. 2.2.10. Коэффициент усиления дисперсии шумов оператором второй производной равен 6 при собственном значении дифференцирования, равном 19.5. Эти значения показывают, что операция двойного дифференцирования может применяться только для данных, достаточно хорошо очищенных от шумов, с основной энергией сигнала в первой трети интервала Найквиста.
В принципе, вторую производную можно получать и последовательным двойным дифференцированием данных оператором первой производной. Однако для таких простых операторов эти две операции не тождественны. Оператор последовательного двойного дифференцирования можно получить сверткой оператора первой производной с самим собой:
2h1 = h1* h1 = {0.25, 0, -0.5, 0, 0.25},
и имеет коэффициент усиления дисперсии шумов всего 0.375. Частотная характеристика оператора:
2H1(w) = 0.5[1-cos(2w)].
Графики 2H1(w) и коэффициента соответствия 2K1(w) приведены пунктиром на рис. 2.2.10. Из их сопоставления с графиками второй производной можно видеть, что последовательное двойное дифференцирование возможно только для данных, спектральный состав которых занимает не более пятой начальной части главного диапазона.
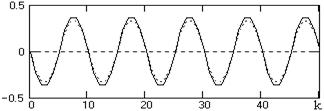 Рис. 2.2.11. Вторая производная гармоники
с частотой w=0.2p при Dt=1 (пунктир – двойное
последовательное дифференцирование)
Рис. 2.2.11. Вторая производная гармоники
с частотой w=0.2p при Dt=1 (пунктир – двойное
последовательное дифференцирование)
|
Пример применения двух операторов второй производной приведен на рис. 2.2.11.
Попутно заметим, что частота Найквиста главного диапазона обратно пропорциональна интервалу Dt дискретизации данных (wN = p/Dt), а, следовательно, интервал дискретизации данных для корректного использования простых операторов дифференцирования должен быть в 3-5 раз меньше оптимального для сигналов с известными предельными частотами спектрального состава.
Частотные функции для третьей производной предлагается получить самостоятельно.
(!!!КР1- Разработка точных простых операторов дифференцирования и методики их расчета)
(!!!КР2- Разработка точных простых операторов вычисления второй производной сигналов и методики их расчета.)
(!!!КР3- Анализ операции вычисления третьей производной данных и повышение точности оператора)
2.3. Интегрирование данных /л24/
Интегрирование сигналов реализуется рекурсивными цифровыми фильтрами. Рассмотрим примеры анализа интегрирующих операторов.
Алгоритм интегрирования по формуле трапеций при нулевых начальных условиях:
yk+1 = yk+(sk+1+sk)/2. (2.3.1)
Принимая sk = exp(jwt) и yk = H(w)exp(jwt), подставляем сигналы в (2.3.1) при tk = kDt, Dt = 1 и решаем относительно H(w). Получаем:
H(w) = (exp(jw)+1)/[2(exp(jw)-1)].
H(w) = cos(w/2)/[2j sin(w/2)].
Истинное значение интеграла равно (1/jw)exp(jwt). Отсюда:
K(w) = H(w)exp(jwt)/[(1/jw)exp(jwt)].
K(w) = cos(w/2)[(w/2)/sin(w/2)]. (2.3.2)
Интегрирование по формуле прямоугольников (интерполяционное среднеточечное). Оператор:
yk+1 = yk+sk+1/2. (2.3.3)
После аналогичных подстановок сигнала и преобразований получаем:
K(w) = (w/2)/sin(w/2).
При численном интегрировании по формуле Симпсона уравнение фильтра имеет вид:
yk+1 = yk-1+(sk+1+4sk+sk-1)/3. (2.3.4)
Частотный анализ фильтра проведите самостоятельно. Контроль:
K(w) = (2+cos w)/[3 sin(w)/w].
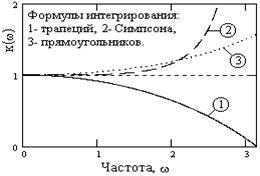 Рис. 2.3.1. Коэффициенты соответствия.
Рис. 2.3.1. Коэффициенты соответствия.
|
Графики функций К(w) приведены на рисунке 2.3.1. При интегрировании происходит накопление результатов по всему предыдущему циклу суммирования и в этих условиях значение коэффициента K(w) является более представительным и информационным, чем передаточная функция оператора для одной текущей точки.
Наиболее простые формулы цифрового интегрирования, трапеций и прямоугольников, ведут себя различным образом в главном частотном диапазоне. Формула прямоугольников завышает результаты на высоких частотах, а формула трапеций - занижает. Эти особенности легко объяснимы. Для одиночной гармоники площадь трапеции по двум последовательным отсчетам всегда меньше, чем площадь с выпуклой дугой гармоники между этими отсчетами, и разница тем больше, чем больше частота. В пределе, для гармоники с частотой Найквиста, отсчеты соответствуют знакочередующемуся ряду (типа 1, -1, 1, -1, ... или любые другие значения в зависимости от амплитуды и начального фазового угла) и при нулевых начальных условиях суммирование двух последовательных отсчетов в формуле (3.2.1) будет давать 0 и накопления результатов не происходит. При интегрировании по площади прямоугольников с отчетом высоты по центральной точке между двумя отсчетами всегда ведет к завышению площади прямоугольника относительно площади, ограниченной выпуклой дугой гармоники.
Формула Симпсона отличается от формул трапеций и прямоугольников более высокой степенью касания единичного значения, что обеспечивает более высокую точность интегрирования в первой половине главного диапазона. Однако на высоких частотах погрешность начинает резко нарастать вплоть до выхода на бесконечность на конце диапазона (полюс в знаменателе передаточной функции рекурсивного фильтра на частоте Найквиста).
Эти особенности интегрирования следует учитывать при обработке данных сложного спектрального состава.
(!!!КР4- Разработка более точного оператора интегрирования и методики его расчета)
Дата добавления: 2020-02-05; просмотров: 735;











