Критические давления, температуры и плотности некоторых веществ
| Вещество | Хими- ческая фор- мула | Атомная масса | Темпе- ратура плавле- ния Тпл, К | Удель- ная тепло- та плав- ния qпл, кДж/ моль | Темпе- ратура кипе- ния Ткип,, К | Удель- ная тепло- та ис- паре- ния r кДж/ моль | Крити- ческое давле- ние Ркр, МПа | Крити- ческая темпе- рату- ра Ткр, К | Крити ческая плот- ность rкр кг/м3 |
| Азот | N2 | 28.0134 | 63.14 | 0.72074 | 77.35 | 5.577 | 3.400 | 126.2 | 313.1 |
| Кислород | О2 | 31.9988 | 54.358 | 0.44 | 90.188 | 6.784 | 5.043 | 154.581 | 436.2 |
| Водород | Н2 | 2.0157 | 13.803 | 0.1174 | 20.28 | 0.8992 | 1.298 | 33.24 | 30.1 |
| Метан | СН4 | 16.0426 | 90.68 | 0.938 | 111.66 | 8.186 | 4.626 | 190.77 | 163.5 |
| Вода | Н2О | 22.115 | 647.3 |
Критические параметры состояния определяются опытным путем. Можно определить критические параметры состояния аналитически, если в уравнении Ван-Дер-Ваальса будут известны величины «а» и «b» для данного вещества. В точке «к» перегиба критической изотермы, как известно из математики, должны быть выполнены условия: первая частная производная 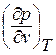 и вторая частная производная
и вторая частная производная 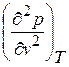 при данной температуре равны нулю. В этом случае получаем соотношения для критических параметров состояния вещества:
при данной температуре равны нулю. В этом случае получаем соотношения для критических параметров состояния вещества: 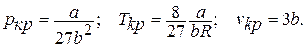
Полученные из опыта критические параметры позволяют вычислить значения величин 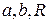 для данного вещества для уравнения Ван-дер-Ваальса:
для данного вещества для уравнения Ван-дер-Ваальса:
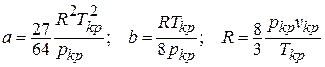
Если соединить линией точки «а"», «а», «а'» и «к» , отвечающие, как указывалось, жидкому состоянию вещества при температурах кипения, то получится плавная кривая, называемая нижней или левой пограничной кривой; на этой кривой при разных давлениях начинается кипение жидкости. Соединение точек «с"», «с», «с’» и «k»дает плавную кривую, которая называется верхней или правой пограничной кривой; на этой кривой при разных давлениях жидкость полностью испаряется, превращаясь в сухой насыщенный пар или, наоборот, если иметь первоначально газ или перегретый пар (например, в точке «2'»), то по линии «с"—с—с’ —к» начнется процесс конденсации, который завершится полностью по линии «а"—а—a’ —k».
Область слева от линии «3—k—а'—а—а" представляет однофазную область жидкого состояния вещества. Область справа от линии «3—к—с’ —с—с"» представляет однофазную область парообразного и газообразного состояния вещества. Области, лежащей между пограничными линиями, соответствует двухфазное состояние вещества в виде влажного насыщенного пара. По линии «3—к» возможно и жидкое, и парообразное состояние.
Если давление 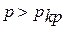 и температура
и температура 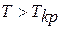 , вещество может находиться только в парообразном или газообразном состоянии.
, вещество может находиться только в парообразном или газообразном состоянии.
Рассмотрим детальнее процесс на участке « 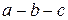 » изотермы «2 – 2’». На рис.1.8 эта изотерма дана для ясности отдельно.
» изотермы «2 – 2’». На рис.1.8 эта изотерма дана для ясности отдельно.
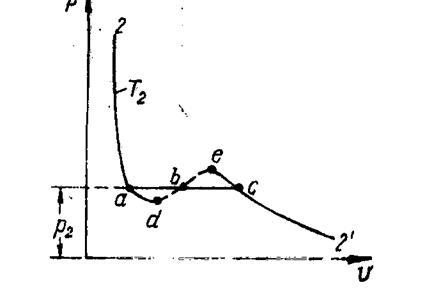
Рис.1.8. Изотерма «2-2, «
Опыт показывает, что в процессе испарения жидкости (или в процессе конденсации пара каждому давлению отвечает определенная температура, зависящая от свойств вещества. Иначе говоря, изотерме 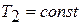 отвечает для данного вещества вполне определенное давление
отвечает для данного вещества вполне определенное давление 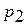 и процесс испарения протекает по горизонтали
и процесс испарения протекает по горизонтали 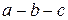 ; процесс конденсации в обратном направлении — по горизонтали
; процесс конденсации в обратном направлении — по горизонтали 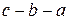 . Следовательно, волнообразная кривая
. Следовательно, волнообразная кривая 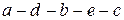 , получаемая по уравнению Ван-дер-Ваальса, не отвечает реальному процессу испарения и конденсации. Вместе с тем на кривой
, получаемая по уравнению Ван-дер-Ваальса, не отвечает реальному процессу испарения и конденсации. Вместе с тем на кривой 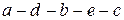 имеются два участка, которые при определенных условиях могут быть получены. Это — участки
имеются два участка, которые при определенных условиях могут быть получены. Это — участки 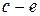 и
и 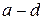 . Если нет в паре центров конденсации, то возможно, что конденсация паров начнется не в точке «
. Если нет в паре центров конденсации, то возможно, что конденсация паров начнется не в точке « 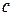 », а в точке «
», а в точке « 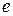 ». На участке
». На участке 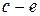 пар является переохлажденным; такое состояние является неустойчивым (метастабильным). Участок
пар является переохлажденным; такое состояние является неустойчивым (метастабильным). Участок 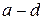 представляет перегретую жидкость; это состояние также возможно, если в жидкости нет растворенных газов других веществ; такое состояние неустойчивое.
представляет перегретую жидкость; это состояние также возможно, если в жидкости нет растворенных газов других веществ; такое состояние неустойчивое.
Появление центров конденсации на участке 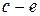 или пузырьков газа или пара на участке
или пузырьков газа или пара на участке 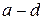 сразу переводит процесс из неустойчивого однофазного состояния в устойчивое двухфазное состояние по горизонтали
сразу переводит процесс из неустойчивого однофазного состояния в устойчивое двухфазное состояние по горизонтали 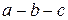 . Что же касается участка
. Что же касается участка 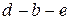 волнообразной кривой, то он невозможен, так как на этом участке при
волнообразной кривой, то он невозможен, так как на этом участке при 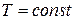 увеличение давления
увеличение давления
одновременно связано с увеличением удельного объёма (то есть 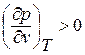 ), что физически нереально.
), что физически нереально.
Уравнение Ван-дер-Ваальса практически охватывает область газообразного и жидкого состояния и даёт представление об области, ограничивающей влажный пар.
1.7. Внутренняя энергия рабочего тела.
Внутренняя энергия системы включает в себя:
- кинетическую энергию поступательного, вращательного и колебательного движения частиц; потенциальную энергию
взаимодействия частиц; энергию электронных оболочек атомов;
внутриядерную энергию.
В большинстве теплоэнергетических процессов две последние составляющие остаются неизменными. Поэтому в дальнейшем под внутренней энергией условимся понимать энергию хаотического движения молекул и атомов, включающую энергию поступательного, вращательного и колебательного движений как молекулярного, так и внутримолекулярного, а также потенциальную энергию сил взаимодействия между молекулами.
Кинетическая энергия молекул является функцией температуры, значение потенциальной энергии зависит от среднего расстояния между молекулами и, следовательно, от занимаемого газом объема V, т. е. является функцией V.
Поэтому внутренняя энергия U есть функция состояния тела.
Для сложной системы внутренняя энергия определяется суммой энергий отдельных частей, то есть обладает свойством аддитивности(от лат. aditivus – прибавляемый, свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, каким бы образом ни был разбит объект).
Величина u = U/M, называемая удельной внутренней энергией (Дж/кг), представляет собой внутреннюю энергию единицы массы вещества.
В дальнейшем для краткости будем называть величину и просто внутренней энергией. Поскольку внутренняя энергия есть функция состояния тела, то она может быть представлена в виде функции двух любых независимых параметров, определяющих это состояние:
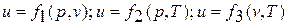 .
.
Ее изменение в термодинамическом процессе 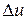 не зависит от характера процесса и определяется только начальным и конечным состояниями тела:
не зависит от характера процесса и определяется только начальным и конечным состояниями тела:
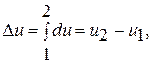 (1.6)
(1.6)
где 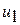 - значение внутренней энергии в начальном состоянии, а
- значение внутренней энергии в начальном состоянии, а 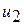 - в конечном. Математически это означает, что бесконечно малое изменение внутренней энергии
- в конечном. Математически это означает, что бесконечно малое изменение внутренней энергии 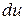 есть полный дифференциал
есть полный дифференциал 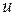 ; если выразить внутреннюю энергию в виде функции удельного объема и температуры, то
; если выразить внутреннюю энергию в виде функции удельного объема и температуры, то
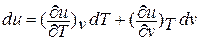
Внутренняя энергия идеального газа, в котором отсутствуют силы взаимодействия между молекулами, не зависит от объема газа или давления
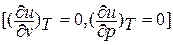 ,
,
а определяется только его температурой, поэтому производная от внутренней энергии идеального газа по температуре есть полная производная:
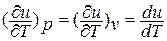
Это положение было впервые установлено Джеймсом Прескоттом Джоулем (1818 – 1889), английским физиком в 1843 году. Принимая теплоемкость не зависящей от температуры, Д.Джоуль вывел формулу для расчета изменения внутренней энергии в термодинамических процессах:
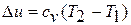 , (1.7)
, (1.7)
где 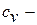 удельная теплоёмкость рабочего тела в процессе при постоянном
удельная теплоёмкость рабочего тела в процессе при постоянном
объёме, 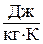 .
.
Для задач технической термодинамики важно знать не абсолютное значение внутренней энергии, а ее изменение в различных термодинамических процессах. Поэтому начало отсчета внутренней энергии может быть выбрано произвольно. Например, в соответствии с международным соглашением для воды за нуль принимается значение внутренней энергии при температуре 0,01 °С и давление 610,8 Па, а для идеальных газов — при 0 °С вне зависимости от давления.
1.8. Теплота рабочего тела.
Помимо макроскопической формы передачи энергии – работы существует также и микроскопическая, то есть осуществляемая на молекулярном уровне форма обмена энергий между рабочим телом и окружающей средой. В этом случае энергия может быть передана рабочему телу без совершения работы. Мерой количества энергии, переданной микрофизическим путем, служит теплота.
Теплота может передаваться либо при непосредственном контакте между телами (теплопроводностью, конвекцией), либо на расстоянии (излучением), причем во всех случаях этот процесс возможен только при наличии разности температур между телами.
Как будет показано ниже, элементарное количество теплоты 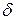 Q, так же как и
Q, так же как и 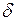 L, не является полным дифференциалом в отличие от дифференциала внутренней энергии dU. За этой математической символикой скрыт глубокий физический смысл различия понятий внутренней энергии, теплоты и работы.
L, не является полным дифференциалом в отличие от дифференциала внутренней энергии dU. За этой математической символикой скрыт глубокий физический смысл различия понятий внутренней энергии, теплоты и работы.
Таким образом, внутренняя энергия — это свойство самой системы, она характеризует состояние системы. Теплота и работа — это энергетические
характеристики процессов механического и теплового взаимодействий системы с окружающей средой. Они характеризуют те количества энергии, которые переданы системе или отданы ею через ее границы в определенном процессе.
1.9. Теплоёмкость рабочего тела.
Теплоёмкостью называют количество теплоты, которое необходимо подвести к рабочему телу, чтобы его температуру повысить на 1 К; точнее - отношение количества теплоты 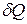 , полученного рабочим телом при бесконечно малом изменении его состояния, к связанному с этим изменением температуры dT называют теплоемкостью рабочего тела :
, полученного рабочим телом при бесконечно малом изменении его состояния, к связанному с этим изменением температуры dT называют теплоемкостью рабочего тела :
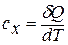 (1.8)
(1.8)
Обозначение 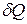 вместо
вместо 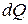 показывает на их различие в зависимости от процесса подвода теплоты. Индекс «х» используется для обозначения того или иного процесса. Например, обозначая
показывает на их различие в зависимости от процесса подвода теплоты. Индекс «х» используется для обозначения того или иного процесса. Например, обозначая 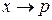 получаем выражение для теплоемкости в изобарном процессе (
получаем выражение для теплоемкости в изобарном процессе ( 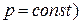 :
:
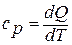
При 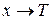 получаем выражение для теплоёмкости в изотермическом процессе (
получаем выражение для теплоёмкости в изотермическом процессе ( 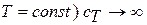 ; при
; при 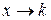 (
( 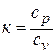 ) получаем
) получаем 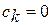 (теплообмен между внешней средой и рабочим телом в адиабатном процессе
(теплообмен между внешней средой и рабочим телом в адиабатном процессе 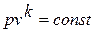 отсутствует); при
отсутствует); при 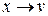 получаем
получаем 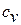 в изохорном процессе (
в изохорном процессе ( 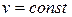 ).
).
Обычно теплоемкость относят к единице количества вещества и в зависимости от выбранной единицы различают:
- удельную массовую теплоемкость 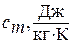 ;
;
- удельную объемную теплоемкость 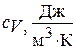 ;
;
- удельную мольную теплоемкость 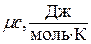 .
.
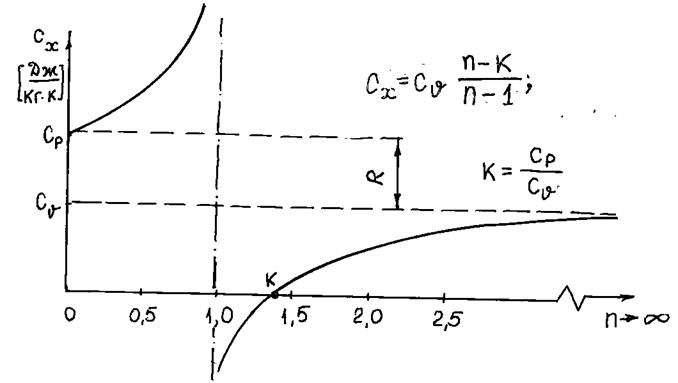
Зависимость теплоемкости от характера процесса может быть представлена графически (рис.1.9).
|
Рис.1.9. Зависимость удельной массовой теплоемкости от показателя
политропы п
Здесь произвольный процесс представляется политропным ( 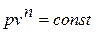 ), где п – показатель политропы, может принимать значения
), где п – показатель политропы, может принимать значения 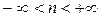 . Теплоёмкость политропного процесса находится по формуле:
. Теплоёмкость политропного процесса находится по формуле:
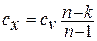 (1.9)
(1.9)
Для идеального газа, молекулы которого имеют массу, бесконечно малые размеры и не взаимодействуют друг с другом (кроме столкновений), существует связь между теплоёмкостями 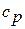 и
и 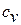 , полученная впервые Юлиусом Робертом Майером (1814 – 1878) – немецким естествоиспытателем и врачом в 1847 году:
, полученная впервые Юлиусом Робертом Майером (1814 – 1878) – немецким естествоиспытателем и врачом в 1847 году:
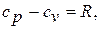 (1.10)
(1.10)
где 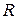 - газовая постоянная. Чем больше
- газовая постоянная. Чем больше 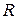 , тем больше требуется работы, например, для сжатия газа в компрессоре газотурбинного двигателя.
, тем больше требуется работы, например, для сжатия газа в компрессоре газотурбинного двигателя.
В изохорном процессе ( 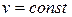 ) теплота, сообщаемая газу, идёт только на изменение его внутренней энергии (впервые установлено в 1843 году английским физиком Джеймсом Прескотт Джоулем (1818 – 1889)). Это видно из дифференциального уравнения первого закона термодинамики:
) теплота, сообщаемая газу, идёт только на изменение его внутренней энергии (впервые установлено в 1843 году английским физиком Джеймсом Прескотт Джоулем (1818 – 1889)). Это видно из дифференциального уравнения первого закона термодинамики:
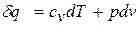 , (1.11)
, (1.11)
где 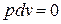 , тогда как в изобарном процессе (
, тогда как в изобарном процессе ( 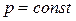 ) теплота расходуется на изменение внутренней энергии и на совершение работы против внешних сил (
) теплота расходуется на изменение внутренней энергии и на совершение работы против внешних сил ( 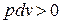 ). Поэтому
). Поэтому 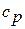 больше
больше 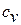 на величину этой работы.
на величину этой работы.
В адиабатном процессе ( 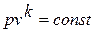 ), протекающем без теплообмена между рабочим телом и внешней средой (
), протекающем без теплообмена между рабочим телом и внешней средой ( 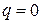 ), отношение теплоёмкостей
), отношение теплоёмкостей  называютпоказателем адиабаты. Для воздуха как идеального газа (доля кислорода в сухом воздухе составляет 20.9476 % , доля азота в воздухе
называютпоказателем адиабаты. Для воздуха как идеального газа (доля кислорода в сухом воздухе составляет 20.9476 % , доля азота в воздухе
78.064 %), теплоёмкость которого не зависит от температуры, 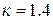 , для продуктов сгорания авиационного керосина
, для продуктов сгорания авиационного керосина 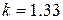 .
.
Величина теплоёмкостей 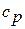 и
и 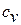 с учётом показателя адиабаты находится из решения системы уравнений:
с учётом показателя адиабаты находится из решения системы уравнений:
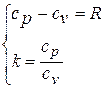
Отсюда
 (1.12)
(1.12)
Для реальных газов 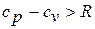 , поскольку при их расширении в изобарном процессе совершается работа не только против внешних сил, но и против сил притяжения, действующих между молекулами, что вызывает дополнительный расход теплоты. При увеличении температуры у многоатомных молекул происходит возбуждение внутренних степеней свободы за счет возникновения колебательного движения атомов молекулы (молекула становится осциллятором). Это приводит к увеличению внутренней энергии, а следовательно, и повышению теплоемкости с ростом температуры.
, поскольку при их расширении в изобарном процессе совершается работа не только против внешних сил, но и против сил притяжения, действующих между молекулами, что вызывает дополнительный расход теплоты. При увеличении температуры у многоатомных молекул происходит возбуждение внутренних степеней свободы за счет возникновения колебательного движения атомов молекулы (молекула становится осциллятором). Это приводит к увеличению внутренней энергии, а следовательно, и повышению теплоемкости с ростом температуры.
Поскольку теплоемкость реального газа зависит от температуры, в технической термодинамике различают истинную и среднюю теплоемкости.
Средняя теплоемкость процесса находится по формуле:
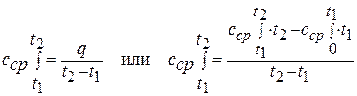 (1.13)
(1.13)
В теплотехнических расчетах теплоемкости 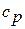 или
или 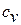 находят по формуле:
находят по формуле:
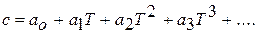
Например, для расчета теплоемкости сухого воздуха рекомендуется следующая формула:
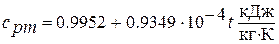
1.10. Уравнение первого закона термодинамики.
Первый закон термодинамики представляет собой частный случай
всеобщего закона сохранения и превращения энергии применительно к тепловым явлениям. В соответствии с уравнением Альберта Эйнштейна
(1879 – 1955), немецкого физика, 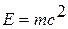 надо рассматривать единый закон сохранения и превращения массы и энергии. Однако в технической термодинамике мы имеем дело со столь малыми скоростями объекта, что дефект массы равен нулю, и поэтому закон сохранения энергии можно рассматривать независимо.
надо рассматривать единый закон сохранения и превращения массы и энергии. Однако в технической термодинамике мы имеем дело со столь малыми скоростями объекта, что дефект массы равен нулю, и поэтому закон сохранения энергии можно рассматривать независимо.
Закон сохранения и превращения энергии является фундаментальным законом природы, который получен на основе обобщения огромного количества экспериментальных данных и применим ко всем явлениям природы. Он утверждает, что энергия не исчезает и не возникает вновь, она лишь переходит из одной формы в другую, причем убыль энергии одного вида дает эквивалентное количество энергии другого вида.
В числе первых ученых, утверждавших принцип сохранения материи и энергии, был наш соотечественник Михаил Васильевич Ломоносов
(1711 — 1765).
Рассмотрим рабочее тело в замкнутой термодинамической системе, например, газ, находящийся под поршнем. Рабочее тело имеет объем V и массу М. Температура рабочего тела Т и давление р. Рабочему телу сообщается извне бесконечно малое количество теплоты 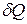 . В результате подвода теплоты тело нагревается на dT и увеличивается в объеме на dV.
. В результате подвода теплоты тело нагревается на dT и увеличивается в объеме на dV.
Повышение температуры тела свидетельствует об увеличении кинетической энергии его частиц. Увеличение объема тела приводит к изменению потенциальной энергии частиц. В результате внутренняя
энергия тела увеличивается на dU. Поскольку рабочее тело окружено внешней средой, которая оказывает на него давление, то при расширении оно производит механическую работу 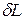 против сил внешнего давления. Так как никаких других изменений в системе не происходит, то по закону сохранения энергии
против сил внешнего давления. Так как никаких других изменений в системе не происходит, то по закону сохранения энергии
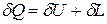 , (1.14)
, (1.14)
то есть теплота, сообщаемая системе, идет на приращение ее внутренней энергии и на совершение внешней работы.
Полученное уравнение является математическим выражением первого закона термодинамики. Каждый из трех членов этого соотношения может быть положительным, отрицательным или равным нулю. Рассмотрим некоторые частные случаи.
1. 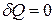 - теплообмен системы с окружающей средой отсутствует, то есть теплота к системе не подводится и от нее не отводится. Процесс без
- теплообмен системы с окружающей средой отсутствует, то есть теплота к системе не подводится и от нее не отводится. Процесс без
теплообмена называется адиабатным. Для него уравнение первого закона принимает вид 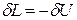 . Следовательно, работа расширения, совершаемая системой в адиабатном процессе, равна уменьшению внутренней энергии данной системы. При адиабатном сжатии рабочего тела затрачиваемая извне работа целиком идет на увеличение внутренней энергии системы.
. Следовательно, работа расширения, совершаемая системой в адиабатном процессе, равна уменьшению внутренней энергии данной системы. При адиабатном сжатии рабочего тела затрачиваемая извне работа целиком идет на увеличение внутренней энергии системы.
2. 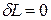 - при этом объем тела не изменяется, dV=0. Такой процесс
- при этом объем тела не изменяется, dV=0. Такой процесс
называется изохорным, для него 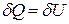 , т.е. количество теплоты, подведенное к системе при постоянном объёме, равно увеличению внутренней энергии данной системы.
, т.е. количество теплоты, подведенное к системе при постоянном объёме, равно увеличению внутренней энергии данной системы.
3. 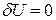 - внутренняя энергия системы не меняется и
- внутренняя энергия системы не меняется и 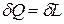 , то есть сообщаемая системе теплота превращается в эквивалентную ей внешнюю работу.
, то есть сообщаемая системе теплота превращается в эквивалентную ей внешнюю работу.
Для системы, содержащей 1 кг рабочего тела первый закон термодинамики в дифференциальной форме имеет вид:
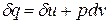 (1.15)
(1.15)
Проинтегрировав это уравнение для некоторого процесса, получим выражение первого закона термодинамики в интегральной форме:
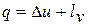 (1.16)
(1.16)
1.11. Уравнение политропного процесса.
Продифференцируем уравнение состояния для 1 кг идеального газа:
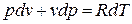
Принимая теплоемкость не зависящей от температуры, получим уравнение первого закона термодинамики в дифференциальной форме:
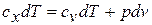
Подставляя в это уравнение выражение для  , получаем
, получаем
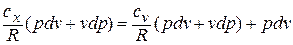
или
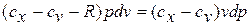
Разделяя переменные и произведя интегрирование, получаем
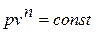 ,
,
где 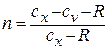 - показатель политропы, может принимать значения от нуля до бесконечности.
- показатель политропы, может принимать значения от нуля до бесконечности.
Зависимость между температурой и удельным объёмом определяется путём замены давления в уравнении политропного процесса его значением из уравнения состояния идеального газа:
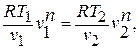
отсюда
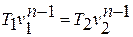 или
или 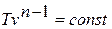
Исключая подобным же образом удельный объём, находим зависимость между давлением и температурой:
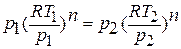 отсюда
отсюда 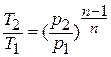 или
или 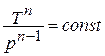
Деформационная работа, производимая 1 кг газа в политропном процессе, определяется по формуле:
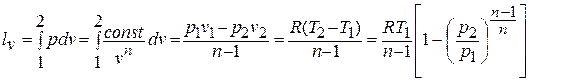 Техническая работа, производимая 1 кг газа в политропном процессе, находится по формуле:
Техническая работа, производимая 1 кг газа в политропном процессе, находится по формуле:
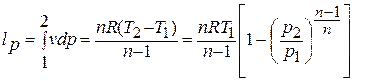
То есть отношение технической и деформационной работ равно показателю политропы:
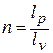
Изменение внутренней энергии в политропном процессе находится общей формулой: 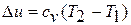
Теплоёмкость процесса  определяется из выражения для показателя политропы:
определяется из выражения для показателя политропы: 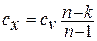
Количество теплоты в политропном процессе находится по формуле:
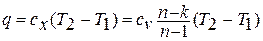
1.12. Энтальпия рабочего тела.
В термодинамике важную роль играет сумма внутренней энергии системы 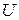 и произведения давления системы
и произведения давления системы 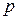 на её объём
на её объём 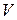 , называемая энтальпией или теплосодержанием и обозначаемая I или Н:
, называемая энтальпией или теплосодержанием и обозначаемая I или Н:
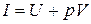
Так как входящие в нее величины являются функциями состояния, то и сама энтальпия является функцией состояния.
Так же как внутренняя энергия, работа и теплота, она измеряется в джоулях (Дж).
Энтальпия обладает свойством аддитивности . Величина
i = u + pv, (1.17)
называемая удельной энтальпией ( 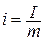 ), представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг.
), представляет собой энтальпию системы, содержащей 1 кг вещества, и измеряется в Дж/кг.
Поскольку энтальпия есть функция состояния, то она может быть представлена в виде функции двух любых параметров состояния:
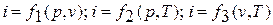 , а величина di является полным
, а величина di является полным
дифференциалом.
Изменение энтальпии в любом процессе определяется только начальным и конечным состояниями тела и не зависит от характера процесса.
Физический смысл энтальпии выясним на следующем примере. Рассмотрим расширенную систему, включающую газ в цилиндре и поршень с грузом общим весом G (рис.1.7). Энергия этой системы складывается из внутренней энергии газа и потенциальной энергии поршня с грузом в поле внешних сил: 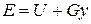 . В условиях равновесия (G = pF) эту функцию можно выразить через параметры газа:
. В условиях равновесия (G = pF) эту функцию можно выразить через параметры газа: 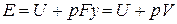 . Получаем, что
. Получаем, что 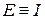 , т.е. энтальпию можно трактовать как энергию расширенной системы.
, т.е. энтальпию можно трактовать как энергию расширенной системы.
Уравнение 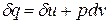 в случае, когда единственным видом работы является работа расширения, с учетом очевидного соотношения
в случае, когда единственным видом работы является работа расширения, с учетом очевидного соотношения 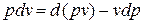 может быть записано в виде
может быть записано в виде 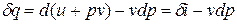 .
.
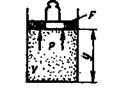
Рис.1.10. К определению физического смысла энтальпии
Из этого соотношения следует, что если давление термодинамической системы сохраняется неизменным, то есть осуществляется изобарный процесс (dp = 0), то 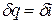 и
и 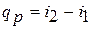 , то теплота, подведенная к системе при постоянном давлении, идет только на изменение энтальпии данной системы.
, то теплота, подведенная к системе при постоянном давлении, идет только на изменение энтальпии данной системы.
Это выражение очень часто используется в расчетах, так как огромное
количество процессов подвода теплоты в теплоэнергетике (в паровых котлах, камерах сгорания газовых турбореактивных двигателей, теплообменных аппаратах), а также целый ряд процессов химической технологии и многих других производствах осуществляется при постоянном давлении. Кстати, по этой причине в таблицах термодинамических свойств обычно приводятся значения энтальпии, a не внутренней энергии.
Для идеального газа для вычисления энтальпии используется формула

Так как между энтальпией и внутренней энергией существует связь, выбор начала отсчета одной из них произволен: в точке, принятой за начало отсчета внутренней энергии, 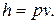 Например, для воды при
Например, для воды при 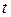 = 0,01 °С ,
= 0,01 °С ,
р = 610,8 Па, 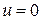 , a
, a 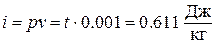 .
.
При расчетах практический интерес представляет изменение энтальпии в конечном процессе:
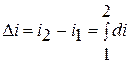
1.13. Энтропия рабочего тела.
Как уже указывалось, величина 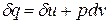 не является полным дифференциалом, так как теплота и изменение внутренней энергии зависят от теплоемкости, которая, в свою очередь, является функцией температуры. Кроме того, чтобы проинтегрировать правую часть этого уравнения, нужно знать зависимость давления от удельного объёма, то есть нужно знать процесс, который совершается.
не является полным дифференциалом, так как теплота и изменение внутренней энергии зависят от теплоемкости, которая, в свою очередь, является функцией температуры. Кроме того, чтобы проинтегрировать правую часть этого уравнения, нужно знать зависимость давления от удельного объёма, то есть нужно знать процесс, который совершается.
В математике доказывается, что дифференциальный двучлен всегда можно превратить в полный дифференциал путем умножения (или деления) на интегрирующий множитель (или делитель). Таким интегрирующим делителем для элементарного количества теплоты 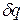 является абсолютная температура Т.
является абсолютная температура Т.
Покажем это на примере изменения состояния идеального газа в равновесных процессах: 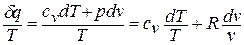
Выражение 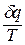 при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния, которая называется энтропией, обозначается для 1 кг газа через
при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния, которая называется энтропией, обозначается для 1 кг газа через 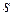 и измеряется в
и измеряется в 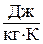 . Термин «энтропия» был введен впервые Рудольфом Юлиусом Эммануэлем Клаузиусом (1822 – 1888), немецким физиком, в 1865 году.
. Термин «энтропия» был введен впервые Рудольфом Юлиусом Эммануэлем Клаузиусом (1822 – 1888), немецким физиком, в 1865 году.
Для произвольного количества газа энтропия, обозначаемая через 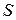 ,
,
равна 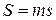 и измеряется в
и измеряется в 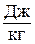 .
.
Таким образом, аналитически энтропия определяется следующим образом: 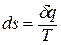
Эта формула справедлива как для идеальных, так и для реальных газов.
Подобно любой другой функции состояния энтропия может быть представлена в виде функции любых двух параметров состояния:
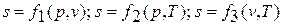
Понятием «энтропия» (от греч. Entropia – поворот, превращение) будем называть в термодинамике направление теплообмена между рабочим телом термодинамической системы и внешней средой.
Значение энтропии для заданного состояния газа определяется интегрированием уравнения для энтропии:
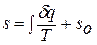 , где
, где 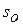 - константа интегрирования.
- константа интегрирования.
При температурах, близких к абсолютному нулю, все известные газы находятся в конденсированном состоянии. Вальтер Нернст (1864 – 1941), немецкий физик и химик, в 1906 году экспериментально установил, а Макс Планк (1858 – 1947), немецкий физик, в 1912 году окончательно сформулировал следующий принцип:
при температуре, стремящейся к абсолютному нулю, энтропия газа, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю,то есть 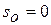 при
при  .
.
Этот закон называют третьим законом термодинамикиили тепловой теоремой В.Нернста. Он позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии, которые всегда отсчитываются от произвольного уровня.
Однако в технической термодинамике обычно используется не абсолютное значение энтропии, а ее изменение в каком-либо процессе:
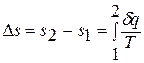 (1.18)
(1.18)
поэтому энтропию тоже отсчитывают от произвольно выбранного уровня.
Получим формулы, позволяющие вычислить изменение энтропии идеального газа. Для этого проинтегрируем уравнение для энтропии, полагая 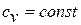 :
:
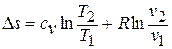
Имея в виду уравнение состояния, записанное для состояний «1» и «2», получаем: 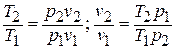
После подстановки отношений 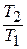 и
и 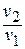 получаем следующие формулы для изменения энтропии идеального газа:
получаем следующие формулы для изменения энтропии идеального газа:
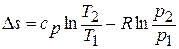 ;
; 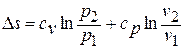
Поскольку энтропия есть функция состояния рабочего тела, написанными уравнениями можно пользоваться вне зависимости от пути перехода рабочего тела между состояниями «1» и «2» и, в частности, от того, равновесный этот переход или нет.
Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов 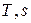 -диаграмму, на которой (как и
-диаграмму, на которой (как и
на 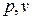 -диаграмме) состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией (рис.1.11).
-диаграмме) состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией (рис.1.11).
Из уравнения для изменения энтропии следует, что в равновесном процессе: 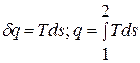 . Очевидно, что в
. Очевидно, что в 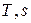 - диаграмме элементарная теплота процесса
- диаграмме элементарная теплота процесса 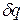 изображается элементарной площадкой с высотой
изображается элементарной площадкой с высотой  и основанием ds, а площадь, ограниченная
и основанием ds, а площадь, ограниченная
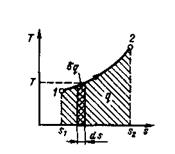
Рис.1.11. Графическое изображение теплоты в 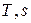 - координатах.
- координатах.
линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.
Формула для элементарного изменения энтропии показывает, что 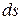 и
и 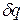 имеют одинаковые знаки, следовательно, по характеру изменения в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты (
имеют одинаковые знаки, следовательно, по характеру изменения в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты ( 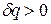 ) его энтропия возрастает (
) его энтропия возрастает ( 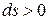 ), а при отводе теплоты (
), а при отводе теплоты ( 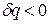 ) убывает (ds<0). При отсутствии теплообмена
) убывает (ds<0). При отсутствии теплообмена 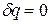 и
и 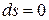 , а равновесный процесс называют адиабатным.
, а равновесный процесс называют адиабатным.
1.14. Исследование термодинамических процессов.
Изменение состояния термодинамической системы во времени называется термодинамическим процессом.
Система, выведенная из состояния равновесия и предоставленная при постоянных параметрах окружающей среды самой себе, через некоторое время вновь придёт в равновесное состояние, соответствующее этим параметрам. Такое самопроизвольное (без внешнего воздействия) возвращение системы в состояние равновесия называется релаксацией, а промежуток времени, в течение которого система возвращается в состояние равновесия, называется временем релаксации.
Термодинамический процесс называется равновесным, если все параметры системы при его протекании меняются достаточно медленно по сравнению с соответствующим временем релаксации.
Рассмотрим, например, процесс сжатия газа в цилиндре. Если время смещения поршня от одного положения до другого существенно превышает
время релаксации, то в процессе перемещения поршня давление и температура успеют выровняться по всему объёму цилиндра. Это выравнивание обеспечивается непрерывным столкновением молекул, в результате чего подводимая от поршня к газу энергия достаточно быстро и равномерно распределяется между ними. Если последующее смещение поршня будет происходить аналогичным образом, то состояние системы в каждый момент времени будет практически равновесным.
Таким образом, равновесный процесс состоит из непрерывного ряда последовательных состояний равновесия, поэтому в каждой его точке состояние можно описать уравнением состояния данного рабочего тела. Именно поэтому классическая термодинамика в своих исследованиях оперирует только равновесными процессами, так как они значительно упрощают решение задачи. Поскольку механические возмущения распространяются в газах со скоростью звука, процесс сжатия газа в цилиндре будет равновесным, если скорость перемещения поршня много меньше скорости звука.
1.14.1. Изобарный процесс.
Если показатель политропы п=0, то из уравнения политропного процесса находим 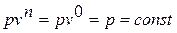 . Таким образом, политропный процесс с показателем п=0 протекает при постоянном давлении; этот процесс называется изобарным. Следовательно, меняются в процессе только температур
. Таким образом, политропный процесс с показателем п=0 протекает при постоянном давлении; этот процесс называется изобарным. Следовательно, меняются в процессе только температур
Дата добавления: 2020-02-05; просмотров: 934;











