Состав сухого воздуха до высоты 90 км
(Литвинов Ю.А., Боровик В.О. Характеристики и эксплуатационные свойства авиационных турбореактивных двигателей. М.:Машиностроение, 1979. 288 с.)
| Наименование составляющей атмосферного воздуха | Хими-ческая форму-ла | Газовая
посто-
янная
R 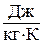
| Масса одного киломо-ля кг/кмоль | Содержа-ние составляю-щей в процентах |
| Азот | N2 | 296.8 | 28.0134 | 78.084 |
| Кислород | O3 | 259.8 | 31.9968 | 20.9476 |
| Аргон | Ar | 208.2 | 39.9440 | 0.934 |
| Углекислый газ | CO2 | 188.9 | 44.0079 | 0.0314 |
| Неон | Ne | 411.9 | 20.1830 | 1.818х10-3 |
| Метан | CH4 | 519.6 | 16.0000 | 0.2х10-3 |
| Сернистый ангидрид | SO2 | 129.8 | 64.0656 | 0.1х10-3 |
| Гелий | He | 2077.2 | 4.0026 | 524х10-6 |
| Криптон | Kr | 99.2 | 83.8000 | 114х10-6 |
| Водород | H2 | 4124.4 | 2.0159 | 50х10-6 |
| Окись азота | N2O | 188.9 | 44.0118 | 50х10-6 |
| Ксенон | Xe | 261.4 | 31.8000 | 8.7х10-6 |
| Озон | O3 | 173.2 | 48.0000 | 7х10-6 (летом) 2х10-6 (зимой) |
| Перекись азота | NO2 | 180.7 | 46.0000 | 2х10-6 |
| Йод | J2 | 65.5 | 126.9044 | 1х10-6 |
1.5. Деформационная и техническая работа идеального газа.
Продифференцируем уравнение состояния для 1 кг массы идеального газа: 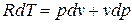
Здесь 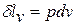 - элементарная работа, связанная с изменением объёма
- элементарная работа, связанная с изменением объёма 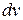 . Эту работу в авиационной технике называют деформационной. Знак «
. Эту работу в авиационной технике называют деформационной. Знак « 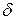 » показывает, что эта работа не является полным дифференциалом, так как неизвестен закон (процесс) изменения давления от удельного объёма (
» показывает, что эта работа не является полным дифференциалом, так как неизвестен закон (процесс) изменения давления от удельного объёма ( 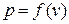 ).
).
Если процесс изменения давления от удельного объёма известен, то есть известен термодинамический процесс 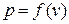 , то интеграл
, то интеграл 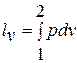 называют деформационной работой или работой сжатия при
называют деформационной работой или работой сжатия при 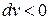 (или расширения при
(или расширения при 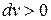 ).
).
Из этой формулы видно, что 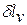 и
и 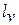 имеют одинаковые знаки:
имеют одинаковые знаки:
если 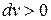 , то
, то 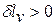 , то есть при расширении деформационная работа рабочего положительна, при этом тело само совершает работу, например, при движении поршня в цилиндре под действием давления газов к так называемой «нижней мёртвой точке»;
, то есть при расширении деформационная работа рабочего положительна, при этом тело само совершает работу, например, при движении поршня в цилиндре под действием давления газов к так называемой «нижней мёртвой точке»;
если 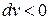 , то
, то 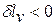 , то есть при сжатии деформационная работа отрицательна: это означает, что на сжатие затрачивается внешняя работа, например, при движении поршня в цилиндре к так называемой «верхней мёртвой точке».
, то есть при сжатии деформационная работа отрицательна: это означает, что на сжатие затрачивается внешняя работа, например, при движении поршня в цилиндре к так называемой «верхней мёртвой точке».
Здесь 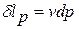 - элементарная работа, связанная с изменением давления
- элементарная работа, связанная с изменением давления 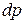 рабочего тела, в том числе и на границе рабочего тела с внешней средой.
рабочего тела, в том числе и на границе рабочего тела с внешней средой.
Знак « 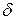 » показывает, что эта работа также не является полным дифференциалом, поскольку неизвестен закон (процесс) изменения давления от удельного объёма (
» показывает, что эта работа также не является полным дифференциалом, поскольку неизвестен закон (процесс) изменения давления от удельного объёма ( 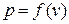 ).
).
Если процесс изменения давления от удельного объёма известен, то есть известен термодинамический процесс 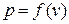 , то интеграл
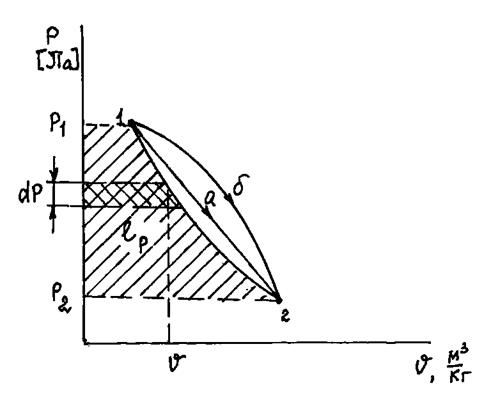
, то интеграл 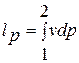 называют технической работой в термодинамическом процессе или интегралом Даниеля Бернулли (1700 – 1782),швейцарского учёного, академика (1725 – 1733) Петербургской Академии наук, разработавшего уравнение в 1738 году, связывающее скорость, давление в потоке идеальной жидкости при установившемся течении и содержащее названный интеграл.
называют технической работой в термодинамическом процессе или интегралом Даниеля Бернулли (1700 – 1782),швейцарского учёного, академика (1725 – 1733) Петербургской Академии наук, разработавшего уравнение в 1738 году, связывающее скорость, давление в потоке идеальной жидкости при установившемся течении и содержащее названный интеграл.
Из этой формулы видно, что 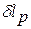 и
и 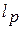 имеют одинаковые знаки:
имеют одинаковые знаки:
если 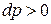 , то
, то 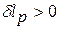 , то есть при увеличении давления рабочего тела техническая работа положительна, за счет подвода внешней энергии к рабочему телу, например, при сжатии воздуха в компрессоре ГТД за счет подводимой внешней энергии от рабочих лопаток;
, то есть при увеличении давления рабочего тела техническая работа положительна, за счет подвода внешней энергии к рабочему телу, например, при сжатии воздуха в компрессоре ГТД за счет подводимой внешней энергии от рабочих лопаток;
если 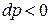 , то
, то 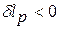 , то есть при уменьшении давления рабочего тела его техническая работа отрицательна: это означает, что рабочее тело отдаёт энергию внешней среде, например, при расширении газа в турбине ГТД, в которой энергия газа передается рабочим лопаткам.
, то есть при уменьшении давления рабочего тела его техническая работа отрицательна: это означает, что рабочее тело отдаёт энергию внешней среде, например, при расширении газа в турбине ГТД, в которой энергия газа передается рабочим лопаткам.
В теплотехнике для исследования термодинамических процессов широко используется 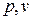 диаграмма, в которой осью абсцисс служит удельный объём
диаграмма, в которой осью абсцисс служит удельный объём 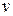 , а осью ординат – давление р (рис.1.4,1.5). Поскольку состояние термодинамической системы определяется двумя параметрами, то на
, а осью ординат – давление р (рис.1.4,1.5). Поскольку состояние термодинамической системы определяется двумя параметрами, то на 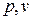 диаграмме оно изображается точкой. На рис.1.4,1.5 точка «1» соответствует начальному состоянию системы, точка «2» - конечному, а линия «12» - процессу расширения (удельный объём возрастает при переходе от
диаграмме оно изображается точкой. На рис.1.4,1.5 точка «1» соответствует начальному состоянию системы, точка «2» - конечному, а линия «12» - процессу расширения (удельный объём возрастает при переходе от 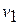 до
до 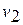 ).
).
|
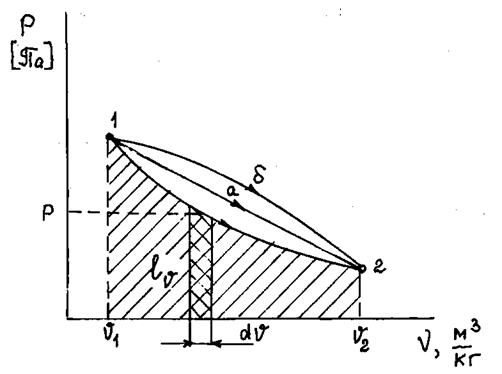
Рис.1.4. Графическое представление деформационной работы расширения
в  диаграмме
диаграмме
|
Рис.1.5. Графическое представление технической работы расширения
в 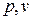 диаграмме
диаграмме
При бесконечно малом изменении удельного объёма 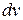 площадь заштрихованной вертикальной полоски равна
площадь заштрихованной вертикальной полоски равна 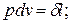 следовательно, работа процесса «12» изображается площадью, ограниченной кривой процесса, осью абсцисс и крайними ординатами. Таким образом, деформационная работа
следовательно, работа процесса «12» изображается площадью, ограниченной кривой процесса, осью абсцисс и крайними ординатами. Таким образом, деформационная работа 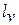 (при изменении объема) эквивалентна площади под кривой процесса в
(при изменении объема) эквивалентна площади под кривой процесса в 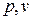 диаграмме. Каждому пути перехода системы из состояния «1» в состояние «2» (например, «12», «1а2» или «1b2») соответствует своя работа расширения:
диаграмме. Каждому пути перехода системы из состояния «1» в состояние «2» (например, «12», «1а2» или «1b2») соответствует своя работа расширения: 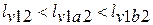 . Следовательно, деформационная работа зависит от характера термодинамического процесса, а не является функцией только исходного и конечного состояний системы. С другой стороны, интеграл
. Следовательно, деформационная работа зависит от характера термодинамического процесса, а не является функцией только исходного и конечного состояний системы. С другой стороны, интеграл 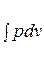 зависит от пути интегрирования и, следовательно, элементарная деформационная работа
зависит от пути интегрирования и, следовательно, элементарная деформационная работа 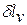 не является полным дифференциалом и не может быть представлена соотношением
не является полным дифференциалом и не может быть представлена соотношением 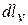 .
.
Дата добавления: 2020-02-05; просмотров: 835;











