Термодинамической системы.

Согласно первому закону термодинамики сообщенное количество теплоты рабочему телу в закрытой термодинамической системе (например,

газ, находящийся в цилиндре поршневого двигателя) идет на увеличение внутренней энергии и на совершение деформационной работы и в дифференциальной форме имеет вид: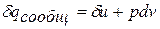

В открытой термодинамической системе (поток воздуха по тракту газотурбинного двигателя) это уравнение преобразуется к виду:

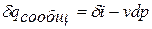
Интегрируя это уравнение от сечения «1-1» до «2-2», получаем:

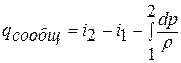
Здесь интеграл в общем случае называют политропной работой или работой расширения (сжатия) против сил давления в движущемся газе.

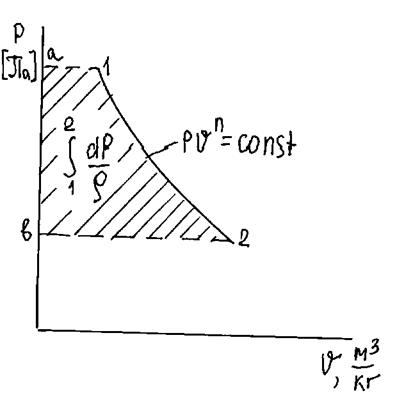
В 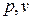- координатах политропная работа изображается площадью 1аb2 (рис.1.20). При отсутствии теплообмена между рабочим телом и внешней средой ( 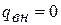) и трения ( 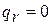) интеграл представляет собой адиабатную работу, которая численно равна изменению энтальпии рабочего тела между сечениями потока:

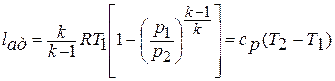
Рис.1.20. Политропная работа в 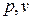координатах

Практический интерес представляет процесс без внешнего теплообмена, но с наличием трения (используется, например, для изучения рабочего процесса в ступени компрессора). Для этого случая, имея в виду, что 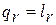, уравнение первого закона термодинамики можно привести в следующему виду:

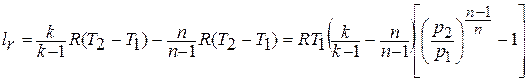
1.18. Обобщенное уравнение Даниила Бернулли (1700 – 1782),

швейцарского академика.

Напишем два уравнения:

1) уравнение сохранения энергии

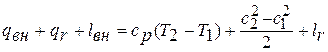
2) уравнение первого закона термодинамики

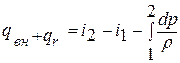
Принимая, что теплоемкость с_р не зависит от температуры, вычитаем из первого уравнения второе. В результате получаем обобщенное уравнение Д.Бернулли: ,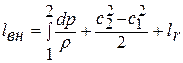

которое гласит: подведенная извне работа расходуется на создание политропной (технической) работы, на приращение кинетической энергии потока и на преодоление сил трения (гидравлических сопротивлений).

Внешний вид уравнения Д.Бернулли не зависит от теплообмена с окружающей средой ( 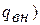. Однако теплообмен оказывает влияние на параметры в конце политропного процесса (через показатель политропы). Например, чем больше показатель политропы отличается от показателя адиабаты, тем больше теплоты подводится к потоку газа.

Если к потоку газа внешняя работа не подводится ( 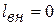), трением можно пренебречь ( 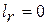), а поток газа движется с небольшой скоростью ( 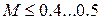), то есть изменением плотности можно пренебречь ( 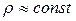), получим уравнение Д.Бернулли для несжимаемой жидкости:

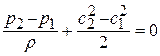или

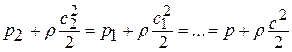
Здесь 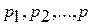- статические давления в сечениях «1-1» , «2-2» и в произвольном сечении потока. Статическим давлениемназывают давление, действующее на измерительную стенку, поставленную параллельно вектору скорости.

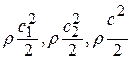- динамические давления или скоростные напоры в соответствующих сечениях потока.

Сумму статического и динамического давления в потоке газаназываютполным давлением или давлением заторможенного потока газа: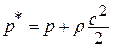

Таким образом, полным давлениемназываютдавление, действующее на измерительную стенку, поставленную перпендикулярно вектору скорости.На основании этого определения полного давления используется для измерения 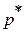трубка Пито - Прандтля, представляющая собой Г- образную трубку, повернутую навстречу потоку.

1.19. Уравнение обращения воздействия.

Прологарифмируем уравнение расхода 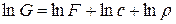, а затем его продифференцируем 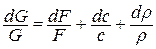, откуда найдем отношение

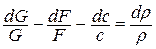
Подставляем полученное выражение в уравнение состояния, написанное в дифференциальной форме:

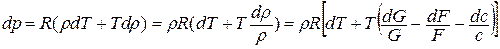
или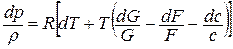

Уравнение Д.Бернулли напишем в дифференциальной форме:

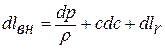
из которого находим отношение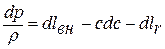

Подставляем значение 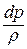в предыдущее равенство:

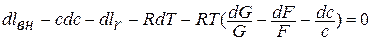
Учитывая, что 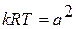, получаем:

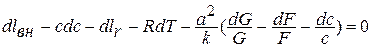
Заменяя в уравнении сохранения энергии в дифференциальной форме:

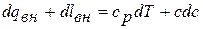
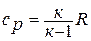и решая это уравнение относительно 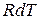, получаем:

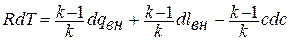
Подставляя полученное выражение в написанное выше уравнение, получаем:

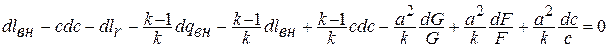
Учитывая соотношение для числа Маха 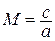, после преобразований получаем окончательно:

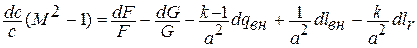
Это соотношение, установленное Л.А. Вулисом, называется условием обращения воздействия. Из соотношения следует, что, например, для увеличения скорости дозвукового потока идеального газа ( 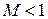, 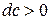) необходимы при отсутствии прочих воздействий нижеперечисленные воздействия.

Каналы, в которых происходит ускорение потока ( 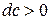), называют конфузорами или соплами.

Каналы, в которых происходит торможение потока ( 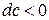), называют диффузорами.

На рис.1.18 – 1.21 показаны различные случаи воздействий для дозвукового ( 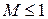) и сверхзвукового ( 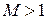) потоков:

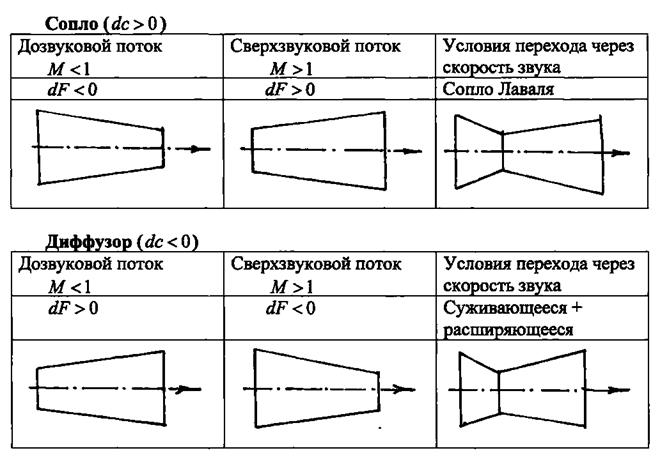
а) геометрическое воздействие;

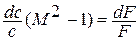
Рис.1.21. Геометрическое воздействие на поток газа

б) расходное воздействие ;

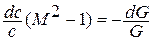
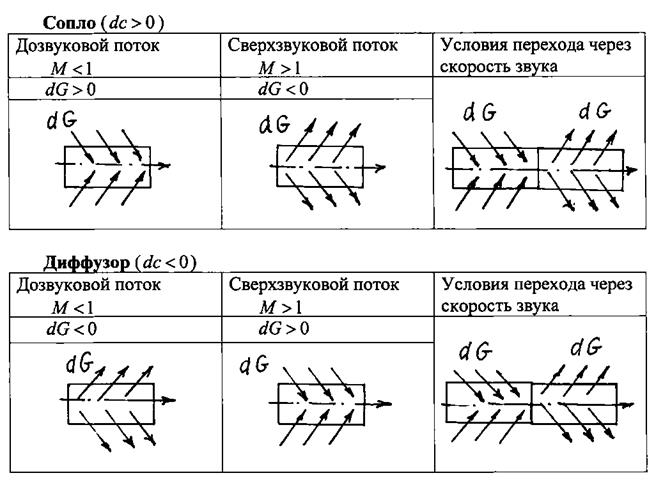
Рис.1.22. Расходное воздействие на поток газа

в) тепловое воздействие (рис.1.23);

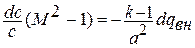
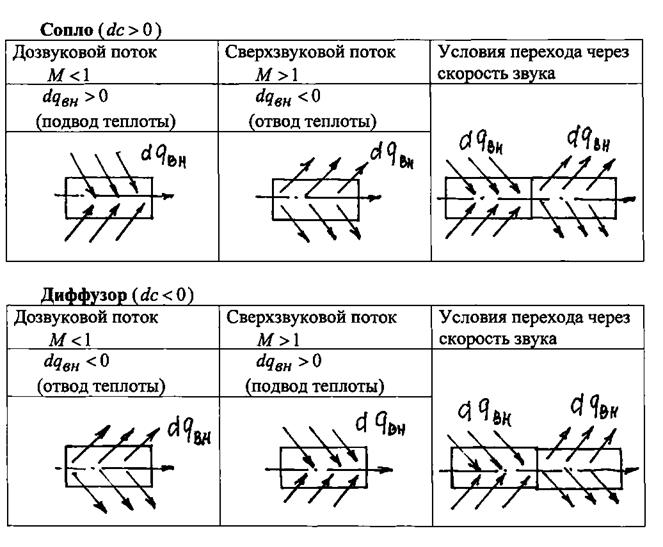
Рис. 1.23. Тепловое воздействие на поток газа

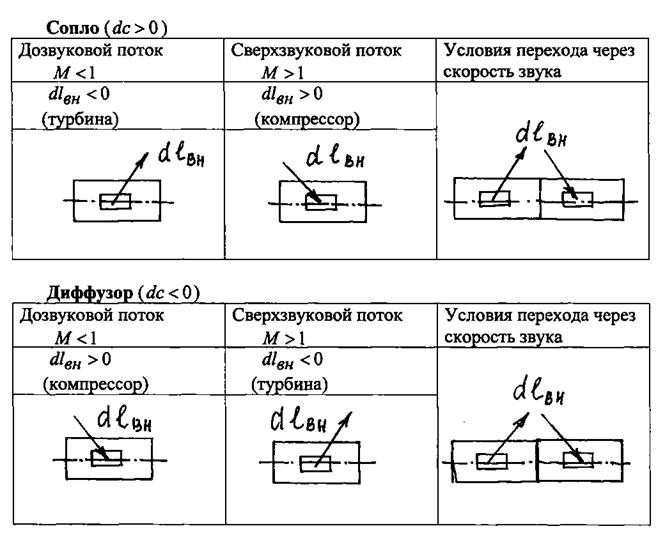
г) механическое воздействие (рис.1.24);

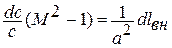
Рис.1.24. Механическое воздействие на поток газа

д) 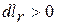(увеличение шероховатости поверхности канала – увеличение трения).

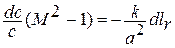
1.20. Теоремы Леонарда Эйлера (1707 – 1783), швейцарского (по происхождению и затем проживавшего в России с 1727 года) математика, физика и астронома, о количестве движения и о моменте количества движения.

Первая теорема «в установившемся потоке равнодействующая всех действующих на трубку тока внешних сил давления и трения равна секундному изменению количества движения вытекающего и втекающего газа».

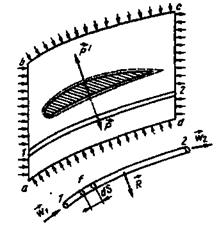
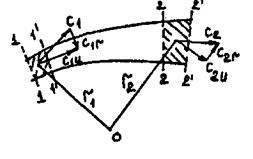
Вторая теорема «в установившемся потоке изменение количества движения секундной массы газа, проходящей через трубку тока, относительно какой-либо произвольной оси равно моменту всех сил, действующих на трубку относительно той же оси».Две теоремы Л.Эйлера (1755 год) являются основополагающими в теории лопаточных машин и реактивных двигателей. Эти теоремы позволяют определить силы и момент сил, действующих на твёрдое тело со стороны обтекающей его жидкости или газа, и наоборот (рис.1.25). В частности, они позволяют определить силы, действующие на лопатки компрессора и турбины газотурбинного двигателя, силу тяги воздушно-реактивного двигателя.

Рис.1.25. К выводу теорем Л.Эйлера о количестве движения

и о моменте количества движения

2. Циклы тепловых машин.

Цикл Карно.

Циклом или круговым процессом тепловых машин называют совокупность термодинамических процессов, в результате совершения которых рабочее тело возвращается в исходное состояние.

В 1824 году французский физик и инженер Карно Никола Леонар Сади (1796 – 1832) впервыепредложил цикл тепловой машины, состоящий из двух адиабатических и двух изотермических процессов (рис.2.1, 2.2).

Рис.2.1. Изображение цикла Карно в 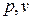координатах:

«1 – 2» - адиабатический процесс сжатия;

«2 – 3» - изотермический процесс расширения – подвод теплоты

к рабочему телу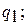

«3 – 4» - адиабатический процесс расширения;

«4 – 1» - изотермический процесс сжатия – отвод теплоты от

рабочего тела

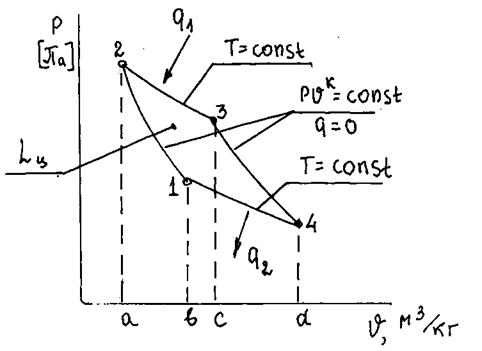
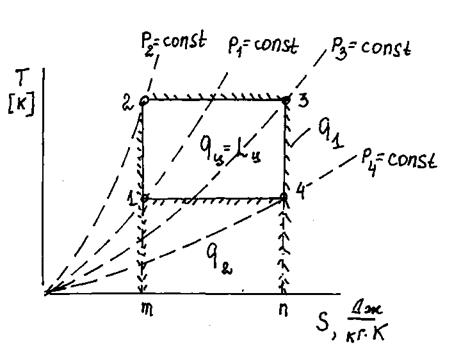
Рис.2.2. Изображение цикла Карно в 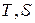координатах

Для расчёта цикла Карно принимаются следующие исходные данные:

- параметры состояния точки «1» (начало цикла): ;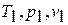

- степень сжатия в адиабатном процессе «1 – 2» ;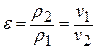

- удельное количество теплоты, подводимое к рабочему телу в изотермическом процессе «2 – 3»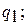

- показатель адиабаты и газовая постоянная рабочего тела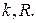

1.Расчет параметров состояния в контрольных точках цикла Карно производится в следующей последовательности:

Точка «2»: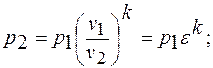

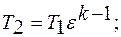
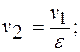
Точка «3»: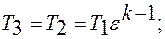

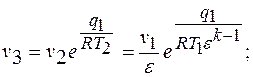
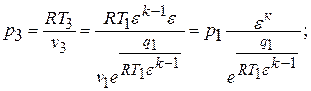
Точка «4»: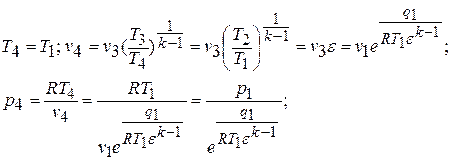

2.Далее производится расчёт энергий, участвующих в термодинамических процессах цикла Карно:

«1 – 2» - адиабатический процесс сжатия

- деформационная работа сжатия, эквивалентная площади фигуры 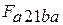на рис.2.1: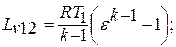

«2 – 3» - изотермический процесс расширения

- деформационная работа расширения, эквивалентная площади фигуры 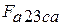на рис.2.1: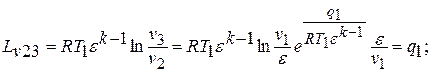

«3 – 4» - адиабатический процесс расширения

- деформационная работа расширения, эквивалентная площади фигуры 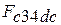на рис.2.1:

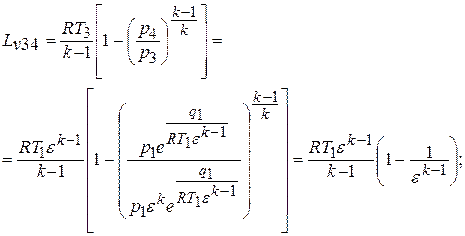
«4 – 1» - изотермический процесс сжатия

- деформационная работа сжатия, эквивалентная площади фигуры 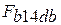на рис.2.1: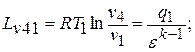

Работа цикла или свободная энергия на выходе из тепловой машины представляет собой алгебраическую сумму деформационных работ цикла

Карно или разность деформационных работ расширения и сжатия. На рис.2.1 работа цикла эквивалентна площади фигуры :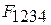

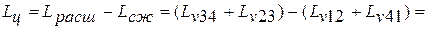
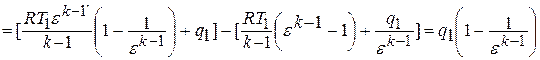
Эффективность цикла Карно оценивается по величине термического коэффициента полезного действия (КПД), определяемого отношением полезной работы цикла 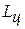к подведенной теплоте :

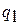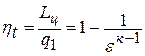
Рассмотрим теперь тепловую диаграмму 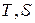(рис.2.2). Термический КПД цикла Карно можно представить так: ,

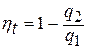где 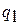- теплота, подведенная к рабочему телу в изотермическом процессе расширения «2 – 3» и эквивалентная площади фигуры 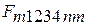на рис.2.2;

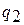- теплота, отведенная от рабочего тела в изотермическом процессе сжатия «4 – 1» и эквивалентная площади фигуры .

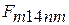В изотермических процессах теплота равна работе процесса, то есть

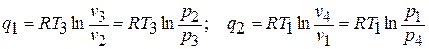
С другой стороны, для адиабатных процессов «1 – 2» и «3 – 4» справедливы зависимости: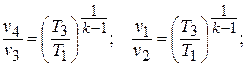

Отсюда 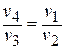или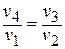

Полезно использованная теплота 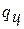в 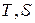диаграмме представляет собой разность подведенной и отведенной теплоты, то есть .

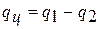На рис.2.2 эта теплота эквивалентна площади фигуры 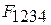, численно равна работе цикла и находится по формуле:

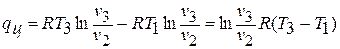
Термический КПД цикла равен отношению полезной теплоты к подведенной, то есть .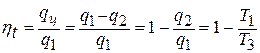

Из полученного выражения для термического КПД цикла Карно следует:

1) термический КПД определяется лишь интервалом температур,

в котором цикл осуществляется;

2) чем ближе значения 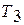и 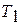, тем меньше термический КПД;

3) термический КПД не может быть равен единице, так как неосуществимо 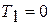ни , ни ;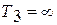

4) при отсутствии тел с разной температурой ( )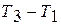

невозможно осуществить периодическое преобразование теплоты в работу;

5) любой произвольный цикл, осуществленный в том же интервале температур 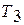и 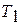, имеет меньший термический КПД, чем КПД цикла Карно.

Это означает, что работа произвольного цикла, эквивалентная площади фигуры 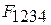, оказывается меньше таковой площади фигуры 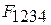для цикла Карно. Поэтому цикл Карно является базовым для всех произвольных циклов, а отношение термического КПД произвольного цикла к термическому КПД цикла Карно (в том же интервале температур) является показателем термодинамического совершенства произвольного цикла.

Приведенное обсуждение для термического КПД цикла Карно позволяет сформулировать второй закон термодинамики или второе начало термодинамики: