Значения показателя политропы.
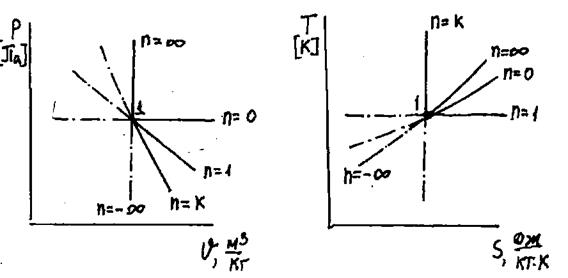
На рис.1.16 и 1.17 показаны различные политропные процессы.
|
Рис.1.16. Изображение различных политропных процессов
в 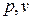 и
и 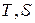 координатах
координатах
|
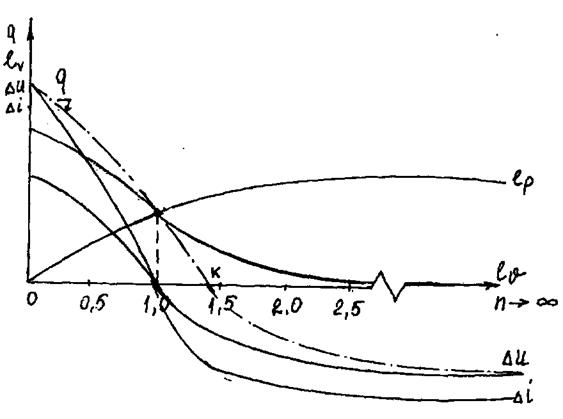
Рис.1.17. Энергии в различных политропных процессах.
Из этих рисунков видно, что существуют три диапазона значений показателя политропы:
1-я группа (0<п<1). Как показывает значение показателя, эти политропные процессы расположены между изобарой и изотермой и протекание их можно определить следующими характеристиками:
а) расширение газа; все процессы на этом участке проходят с повышением температуры и, следовательно, с увеличением внутренней энергии газа; объем газа увеличивается, т. е. газ расширяется и совершает деформационную работу. Таким образом, процесс проходит с подводом к газу теплоты, которая частично расходуется на нагрев газа и частично на работу расширения. По мере приближения значения показателя к единице часть теплоты, расходуемой на изменение внутренней энергии газа, приближается к нулю, температура уменьшается;
б) сжатие газа; вполне понятно, что все явления при сжатии газа проходят с обратным знаком. Объем газа уменьшается и на сжатие газа затрачивается работа; температура газа понижается и внутренняя энергия его уменьшается. Таким образом, от газа должна быть отведена теплота, полученная от убыли внутренней энергии и от работы, затраченной на сжатие газа.
Теплоемкость процессов меняется от 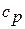 (при
(при 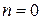 ) до
) до 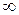 (при
(при 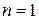 ). Значение коэффициента
). Значение коэффициента 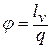 меняется от l/k (при
меняется от l/k (при 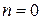 ) до 0 (при
) до 0 (при 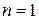 ).
).
2-я группа (1<n<k). Эти процессы располагаются между изотермой и адиабатой:
а) расширение газа; при изотермическом расширении работа получается за счет теплоты, подводимой извне; при адиабатном расширении работа совершается только за счет внутренней энергии газа. В процессах, расположенных между изотермой и адиабатой, работа газа совершается частично за счет теплоты, подведенной извне, частично за счет внутренней энергии газа; чем ближе значение п к единице, тем большая доля работы совершается за счет внешней теплоты; чем ближе значение п к значению k, тем большая доля работы совершается за счет убыли внутренней энергии газа, тем сильнее охлаждается газ;
б) сжатие газа; так как все явления проходят с обратным знаком, то в процессе сжатия частично увеличивается внутренняя энергия газа и теплота должна частично отводиться в окружающую среду; чем ближе значение п к единице, тем больше отводится теплоты в окружающую среду и тем меньше нагревается газ. В этих процессах теплоемкость имеет отрицательное значение и меняется от 0 до 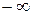 , что видно из уравнения
, что видно из уравнения 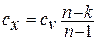 , где при n=k (адиабата)
, где при n=k (адиабата) 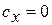 , а при
, а при 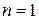
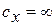 (изотерма).
(изотерма).
Отрицательное значение теплоемкости в этих процессах вполне объяснимо. Действительно, теплоемкость процесса определяет количество теплоты, которое необходимо подвести к газу в процессе для повышения его температуры на один градус; но нагрев можно осуществить не только подводом теплоты, но и в процессе сжатия газа.
В политропных процессах, расположенных между изотермой и адиабатой, при расширении газа работа совершается частично за счет внутренней энергии, и температура газа падает, но остальная, необходимая для работы теплота подводится из окружающей среды. Таким образом, при расширении, несмотря на подвод теплоты, газ охлаждается, что возможно только при отрицательном значении теплоемкости. Это видно из уравнения 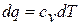 , где dq>Q, a dT<0.
, где dq>Q, a dT<0.
Такое же явление происходит и при сжатии газа; работа сжатия превращается в теплоту, но часть этой теплоты отводится в окружающую среду и только часть ее идет на нагрев газа. Следовательно, температура газа повышается при отводе теплоты и в приведенном уравнении 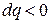 и
и 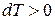 , что возможно только при отрицательном значении теплоемкости.
, что возможно только при отрицательном значении теплоемкости.
Значение величины 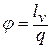 меняется от 0 при п=1 до оо при n=k.
меняется от 0 при п=1 до оо при n=k.
3-я группа (к<п< 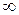 ). Эти процессы расположены между адиабатой и изохорой. Кривые процесса по мере увеличения значения п располагаются все более круто, приближаясь в пределе к прямой
). Эти процессы расположены между адиабатой и изохорой. Кривые процесса по мере увеличения значения п располагаются все более круто, приближаясь в пределе к прямой 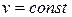 :
:
а) расширение газа; работа газа все время уменьшается, приближаясь к нулю (изохора); отводимое количество теплоты возрастает вследствие убыли внутренней энергии, и поэтому температура газа понижается быстрее;
б) сжатие газа; несмотря на то что работа сжатия газа уменьшается, температура его увеличивается по мере приближения значения п к 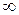 , так как количество теплоты, подводимое извне, все увеличивается; увеличение внутренней энергии газа происходит за счет суммарной теплоты, подводимой извне, и эквивалентной работы сжатия.
, так как количество теплоты, подводимое извне, все увеличивается; увеличение внутренней энергии газа происходит за счет суммарной теплоты, подводимой извне, и эквивалентной работы сжатия.
Теплоемкость в процессах по мере увеличения показателя политропы п от k до 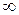 увеличивается от 0 до
увеличивается от 0 до 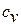 , что видно из уравнения
, что видно из уравнения 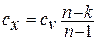 . Значение коэффициента
. Значение коэффициента 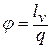 от
от 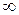 (при n=k) уменьшается до 1 (при
(при n=k) уменьшается до 1 (при 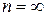 ). В этом можно убедиться, если уравнение
). В этом можно убедиться, если уравнение 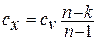 представить в следующем виде, полученном после деления числителя и знаменателя на п, причем при
представить в следующем виде, полученном после деления числителя и знаменателя на п, причем при 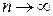 .
.
Из рис.1.17 можно сделать еще следующие выводы. Так как изотермы по мере удаления от начала координат характеризуют все более высокие температуры, то все процессы, идущие от начальной точки 1 вверх и вправо от изотермы, проходят с повышением температуры газа, то есть увеличением его внутренней энергии. Процессы, идущие от начальной точки 1 вниз и влево, проходят с понижением температуры газа и, следовательно, с уменьшением его внутренней энергии.
Таким образом, изотерма является границей процессов, проходящих с увеличением и уменьшением внутренней энергии газа.
Если рассматривать адиабату как границу процессов, то можно убедиться, что все процессы, проходящие вверх и вправо от адиабаты, идут с подводом теплоты, а идущие вниз и влево - с отводом теплоты в окружающую среду.
1.15. Уравнение сохранения энергии для потока газа.
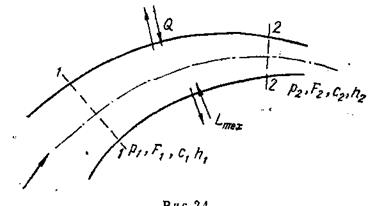
Рассматривается открытая термодинамическая система – поток движущегося газа (рис.1.18). Рабочее тело с массовым расходом 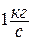 , перемещаясь от сечения «1-1» к сечению «2-2», характеризуется следующими видами изменения энергий:
, перемещаясь от сечения «1-1» к сечению «2-2», характеризуется следующими видами изменения энергий:
- внутренней энергии газа 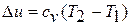 ;
;
- кинетической энергии газа 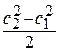 ;
;
- энергии положения относительно уровня моря 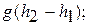
|
Рис.1.18. Поток газа
- энергии проталкивания газа 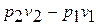
Все перечисленные изменения энергии были получены за счёт подвода потока извне теплоты 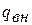 и внешней работы
и внешней работы 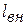 . Таким образом, получаем уравнение сохранения энергии в общем виде:
. Таким образом, получаем уравнение сохранения энергии в общем виде:
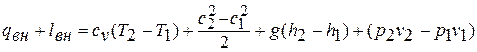 (1.19)
(1.19)
При движении газа по каналу имеет место трение, на преодоление которого затрачивается работа 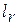 , которая эквивалентна количеству теплоты, подводимой к потоку из-за трения
, которая эквивалентна количеству теплоты, подводимой к потоку из-за трения 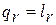 . Отсюда уравнение сохранения энергии с учётом трения записывается так:
. Отсюда уравнение сохранения энергии с учётом трения записывается так:
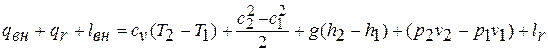
Сумма 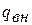 и
и 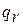 называется сообщенной теплотой потоку газа:
называется сообщенной теплотой потоку газа:
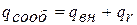 .
.
Изменением энергии положения 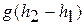 обычно пренебрегают ввиду малого отличия геометрических высот относительно уровня моря
обычно пренебрегают ввиду малого отличия геометрических высот относительно уровня моря 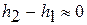 .
.
Изменение энергии проталкивания 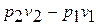 на основании уравнения состояния газа можно записать
на основании уравнения состояния газа можно записать 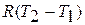 , а сумма
, а сумма 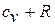 на основании уравнения Майера равна
на основании уравнения Майера равна 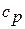 . В этом случае уравнение сохранения энергии имеет вид:
. В этом случае уравнение сохранения энергии имеет вид: 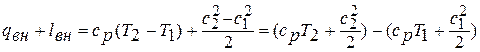
Сумма энтальпии 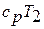 и кинетической энергии
и кинетической энергии 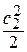 в сечении называется полной энергией или полной энтальпией
в сечении называется полной энергией или полной энтальпией 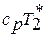 . Отсюда уравнение сохранения энергии можно трактовать так: подведенные извне теплота и работа расходуются на изменение полной энергии потока:
. Отсюда уравнение сохранения энергии можно трактовать так: подведенные извне теплота и работа расходуются на изменение полной энергии потока:
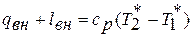
Для произвольного сечения потока выражение для полной энергии записывается в виде: 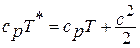 или
или 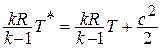
Разделим обе части уравнения на 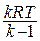 :
: 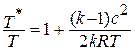
Из курса физики известно, что 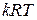 равно квадрату скорости звука а2, а отношение скорости к скорости звука называется числом Маха
равно квадрату скорости звука а2, а отношение скорости к скорости звука называется числом Маха 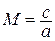 .
.
Данное отношение названо в честь Эрнста Маха (1838 – 1916), австрийского физика и философа; отношение является критерием( от греч. Kriterion – средство для суждения) – признаком, на основании которого производится оценка, определение или классификация чего - либо; мерило оценки; в данном случае критерий сжимаемости газа. Формула 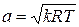 получается при допущении, что звуковая энергия (волна) распространяется в газе или жидкости в соответствии с уравнением адиабатного процесса
получается при допущении, что звуковая энергия (волна) распространяется в газе или жидкости в соответствии с уравнением адиабатного процесса 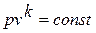 или
или 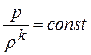 .
.
Дифференциальное уравнение этого процесса представляется так 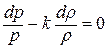 , или
, или 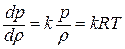 . Отношение
. Отношение 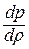 соответствует величине звуковой энергии (квадрату скорости распространения звука в веществе).
соответствует величине звуковой энергии (квадрату скорости распространения звука в веществе).
Отсюда выражение для полной энергии потока в сечении записывается так: 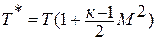
Число Маха, таким образом, является характеристикой сжимаемости рабочего тела. Например, при 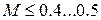 сжимаемостью газа можно пренебречь и принять
сжимаемостью газа можно пренебречь и принять 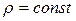 , то есть считать газ как жидкость. При
, то есть считать газ как жидкость. При 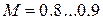 - околозвуковой поток, характерный для полетов гражданских самолетов; при
- околозвуковой поток, характерный для полетов гражданских самолетов; при 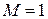 - звуковой барьер или критический режим течения потока; при
- звуковой барьер или критический режим течения потока; при 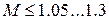 - трансзвуковой поток, характерный режим обтекания некоторых участков крыла самолета даже при околозвуковой скорости полета воздушного судна; при
- трансзвуковой поток, характерный режим обтекания некоторых участков крыла самолета даже при околозвуковой скорости полета воздушного судна; при 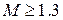 - сверхзвуковой поток; при
- сверхзвуковой поток; при 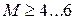 гиперзвуковой поток. Поскольку плотность воздуха в атмосфере Земли с высотой уменьшается практически до нуля, то число Маха в полете при этих условиях стремится к бесконечности (например, поток газа в пустоту).
гиперзвуковой поток. Поскольку плотность воздуха в атмосфере Земли с высотой уменьшается практически до нуля, то число Маха в полете при этих условиях стремится к бесконечности (например, поток газа в пустоту).
Принимая 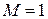 , находим критическую скорость звука, используя выражение:
, находим критическую скорость звука, используя выражение: 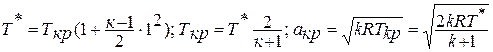
Если формулу для полной энергии потока разделить на 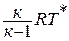 и обозначить отношение скорости к критической скорости звука как приведенную скорость
и обозначить отношение скорости к критической скорости звука как приведенную скорость 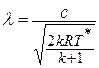 , то выражение для полной энергии потока в сечении (или для любой точки потока) представляется так
, то выражение для полной энергии потока в сечении (или для любой точки потока) представляется так
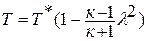 или
или 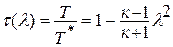 - газодинамическая функция температуры. Значение приведенной скорости меняется от нуля до максимального значения
- газодинамическая функция температуры. Значение приведенной скорости меняется от нуля до максимального значения 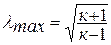 .
.
Если принять процесс торможения потока от температуры 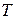 до
до 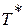 адиабатным, что практически соответствует приборам для измерения давления в потоке, то можно найти выражение для газодинамической функции давления
адиабатным, что практически соответствует приборам для измерения давления в потоке, то можно найти выражение для газодинамической функции давления 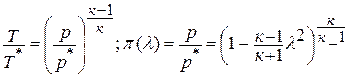
или плотности 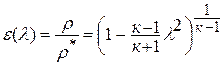 .
.
Уравнение сохранения энергии широко используется в авиационной практике для различных элементов двигателей. Например:
а) работа , подводимая к валу ротора компрессора 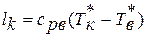 ;
;
Дата добавления: 2020-02-05; просмотров: 1011;











