Проекция вектора на ось.

Пусть l – некоторая прямая в пространстве. Выберем точку OÎ l и единичный вектор ||l.Построим направленный отрезок = . Прямая l с отрезком называется осью. Иногда говорят, что ось – это прямая, на которой задано направление.

Определение. Пусть – произвольный вектор, а – произвольный направленный отрезок, который представляет . Опустим перпендикуляры AA₁ и BB₁ на прямую l. Пусть = . Тогда вектор

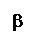
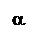
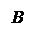
называется векторной проекцией вектора на ось l и обозначается p_l.

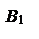
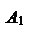
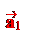
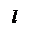
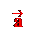
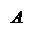
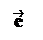
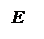
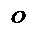
Мы имеем ||. Поэтому согласно теореме 1 существует такое число p, что = p. Это число называется скалярной проекцией вектора на ось l . Поскольку –

единичный вектор, то p – это длина вектора , если ­­, и p = – ||, если ­¯. Будем обозначать скалярную проекцию так: P_l.

Зная скалярную проекцию вектора мы можем найти его векторную проекцию:

p_l = (P_l ); (*)

Если ^, то, очевидно, A₁= B₁ и P_l = 0.

Необходимо еще доказать, что определения скалярной и векторной проекции корректны, т.е. не зависят от выбора направленного отрезка , который представляет вектор . Другими словами, если мы отложим вектор от другой точки, то его скалярная и векторная проекции не изменятся,– и это надо доказать.

Проведем через точки A и B плоскости a и b перпендикулярно l. Тогда ½p½=½P_l½ есть расстояние между a и b .Выберем другой направленный отрезок , представляющий и проведем через точки A¢, B ¢ плоскости a¢ и b¢ перпендикулярно l. Направленные отрезки и эквивалентны, а значит, они совмещаются параллельным переносом. При этом переносе плоскость a совместится с a¢, а плоскость b – с b¢. Значит, расстояние между a¢ и b¢ равно расстоянию между a и b, и оно равно ½p½. Поэтому ½p½ не зависит от выбора направленного отрезка. Направление векторной проекции также не изменится при переносе, поэтому и знак p не изменится. Итак, скалярная проекция не зависит от выбора направленного отрезка, представляющего . В силу равенства (*) p_l также не зависит от выбора направленного отрезка.

Теорема 2. Свойства проекции вектора на ось.

1.P_l =| |cosÐ(, );

2.P_l(l ) = lP_l , p_l(l ) = l(p_l );

3.P_l( + ) = P_l + P_l, p_l( + ) = p_l + p_l .

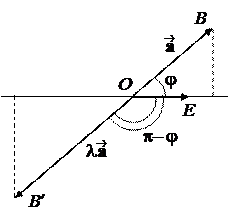
Доказательство. 1. Поскольку определение проекции не зависит от выбора точки A ,из которой отложен вектор , мы можем отложить его из точки О. Обозначим j =Ð(, ).

1 случай: j £ p/2. Тогда из DOBB₁ получим, что

p =½OB₁½=½OB½· cos j = | |cos j.

2 случай: j > p/2. Тогда из DOBB₁ получим, что

p = –½OB₁½= –½OB½· cos (p– j) = | |cos j.

2. Для скалярных проекций:

1 случай: l > 0. Тогда l ­­ и Ð(, l ) = j. Значит,

P_l(l ) =½l½cos Ð(,l ) =

= l| |cos j = lP_l .

2 случай: l < 0. Тогда l ­¯ ,

Ð(, l ) = p – j и cosÐ(,l ) = – cos j,

P_l(l ) =½l½cosÐ(,l ) = –l| |(– cos j) =

= l| |cosÐ(, ) = lP_l .

3случай: l = 0. Тогда равенство очевидно.

Для векторных проекций с помощью равенства (*) получаем:

p_l(l ) = (P_l(l )) · = l(P_l ) · = l(p_l ).

3.Доказательство для векторных проекций показано на чертеже, но только для случая векторов на плоскости. Рисунок для векторов в пространстве можно найти в учебнике [10].

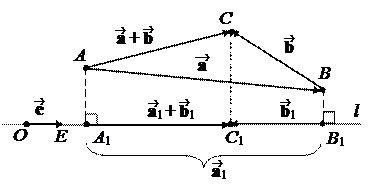Для скалярных проекций равенство вытекает из равенства для векторных проекций. Например, в случае, изображенном на втором рисунке,

P_l( + ) = |A₁C₁|,

P_l = |A₁B₁|,

P_l = – |B₁C₁|,

и мы видим, что

|A₁C₁|= |A₁B₁|+(– |B₁C₁|).