Угол между векторами. Ориентация пары векторов на плоскости или тройки векторов в пространстве.

Определение. Пусть и – два ненулевых вектора. Отложим их из одной точки О: = , = . Тогда углом между векторами и называется угол между лучами OA и OB, т.е. a =ÐAOB. Пишем a =Ð( , ).

Если речь идет о векторах на плоскости, то можем ввести понятие ориентированного угла между векторами. Если кратчайший поворот

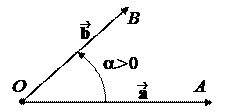от луча OA к лучу OB осуществляется против часовой стрелки, то считаем, что a > 0, а если по часовой – то a < 0 . Таким образом, – p < a £ p . Если a > 0, то пара векторов (, ) называется правой, а если a < 0 – то левой.

В пространстве понятие ориентированного угла не имеет смысла. Если посмотреть на плоскость, в которой лежат лучи OA и OB с одной стороны, то увидим, что кратчайший поворот от OA к OB осуществляется в одном направлении, а если посмотреть на плоскость с другой стороны, то мы увидим тот же поворот в другом направлении.

Пусть в пространстве даны три некомпланарных вектора , , . Отложим их из одной точки О: = , = , = . Тройка векторов (, , ) называется правой, если кратчайший поворот от луча OA к лучу OB, если смотреть из точки C , выглядит как осуществляющийся против часовой стрелки. Соответственно, если этот поворот выглядит как осуществляющийся по часовой стрелке, то тройка векторов (, , ) называется левой. На рисунке изображена правая тройка векторов.