Свойства операции умножения вектора на число.

1.l( + ) = l + l; 3.(l + m) = l + m;

2.l(m ) = (lm); 4.1· = .

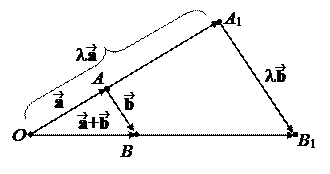Доказательство. 1.Пусть

= , = ,

l= , l = .

Тогда по правилу треугольника

+ = , l + l = .

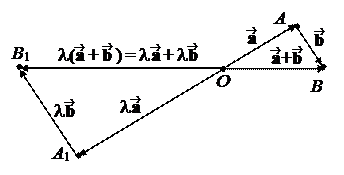Нам требуется доказать, что l( + ) = .

Из (**) вытекает по-добие треугольников ΔOAB ~ ~ ΔOA₁B₁ по двум сторонам и углу между ними. Поэтому | | и ||= l||.

Отсюда, с учетом + = , вытекает l( + ) = . На первом рисунке изображен случай l > 0, а на втором – l < 0. В случае же l = 0, обе части равенства дают .

Упражнение. Остальные свойства докажите самостоятельно.

Теорема 1(первый признак коллинеарности векторов). Для того, чтобы ненулевые векторы и были коллинеарны, необходимо и достаточно, чтобы существовало такое число l , что = l.

Доказательство. Достаточность вытекает непосредственно из определения произведения вектора на число. Если = l, то по определению ||.

Необходимость. Пусть ||.

1 случай: ­­ . Положим l =½½ /½½ > 0. Тогда

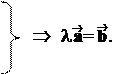l ­­ Þ l ­­ ,

½l½ =½l½½½ = l| |= | |=½½.

2 случай: ­¯ . Положим l = –½½ /½½ < 0. Тогда

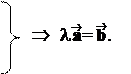l ­¯ Þ l ­­ ,

½l½ =½l½½½= –l| |= | |=½½.

Что и требовалось доказать.

В процессе доказательства мы показали, как решить следующую задачу: найти вектор сонаправленный с данным вектором и имеющий заданную длину ½½= b. Это будет вектор = . В частности, единичный вектор ­­ находится так: = . Такой вектор называется ортом вектора .