Свойства операции сложения векторов.

" , , выполнено

1. + = + (коммутативность);

2. (+)+=(ассоциативность);

3.+ = .

4.$! такой что + =. Этот вектор называется противоположным вектором к и обозначается –.

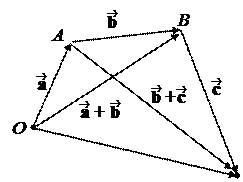
Доказательство. 1. Отложим и от одной точки O: =, =. Достроим ΔOAB до параллелограмма OACB. Пусть =. Очевидно, что ~, т.е. =. Тогда по правилу треугольника + =. С другой стороны, ~, Þ = и по правилу треугольника + =.

Данный способ построения суммы векторов называется правилом параллелограмма.

2.Доказательство обозначено на чертеже. Здесь мы видим, что с одной стороны, (+)+= =, а с другой стороны, +(+)=.

Это свойство позволяет использовать обозначение ++ без расстановки скобок.

3.Пусть =, а можем задать с помощью направленного отрезка . Тогда по правилу треугольника + = . Значит, +=.

4. Пусть = . Зададим = . Тогда по правилу треугольника + = . Значит, += . Тем самым мы доказали существование противоположного вектора. Докажем единственность.

Предположим, что существует еще один вектор такой что +=. Прибавим к последнему равенству справа и слева вектор :

(+)+=+.

Используя свойства 1 и 2 получаем

(+)+=+ Þ + = + Þ = .

Определение. Разностью двух векторов и называется такой вектор , что +=. Пишем = –.

Докажем, что разность векторов существует и определяется однозначно.

Отложим и от одной точки O: = , =, и пусть =. Тогда по правилу треугольника += (*). Значит, разность двух векторов существует.

Докажем единственность. Прибавим справа и слева к к равенству (*) вектор –:

(+)+(–)=+(–).

Используя свойства 1 и 2 получаем

+=+(–) Þ =+(–).

Тем самым мы доказали, что –=+(–). А поскольку единственность противоположного вектора мы уже доказали, то и разность определяется однозначно. Кроме того, мы увидели, как построить разность на чертеже.

Определение. Произведением векторана число l называется такой вектор , что

1. , если l >0, и ¯, если l<0 ;

2. | |= |l|·| |.

Пишем = l. (Часто еще добавляют 3.если l =0, то =. Но это следует из 2.)