Ряд, членами которого являются степенные функции, называется степенной

,

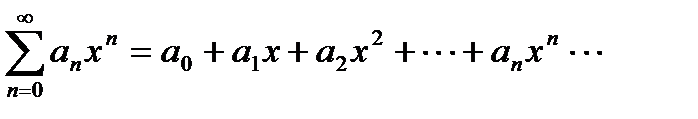где числа а₀, а₁, ¼ а_п называются коэффициентами ряда.

При x = x₀ степенной ряд превращается в числовой ряд. Если полученный числовой ряд сходится, то точка x₀ называется точкой сходимости ряда, если ряд расходится – точкой расходимости.

Совокупность числовых значений x, при которых степенной ряд сходится, называется его областью сходимости.

Теорема Абеля

Если степенной ряд сходится при x = x₀ ¹ 0, то он абсолютно сходится при всех значениях |x| < |x₀|.

Следствие: Если ряд расходится при x = x₁, тоон расходится и при всех |x| > |x₁|.

Из теоремы Абеля следует, что если x₀ ¹ 0 есть точка сходимости степенного ряда, то интервал (– |x₀|;|x₀|)весь состоит из точек сходимости данного ряда; при всех значениях x вне этого интервала степенной ряд расходится.

Интервал (– |x₀|;|x₀|)называется интервалом сходимости степенного ряда. Число R = |x₀|называется радиусом сходимости степенного ряда, т.е. при всех x, для которых |x| < R, ряд абсолютно сходится, а при |x| > R ряд расходится.

В частности, когда степенной ряд сходится лишь в одной точке x₀ = 0, то считается, что R = 0. Если же ряд сходится при всех значениях x Î R (т.е. во всех точках числовой оси), то считается, что R = ∞.

Отметим, что на концах интервала сходимости (т.е. при x = R и при x = – R) сходимость ряда проверяется в каждом конкретном случае отдельно.

Согласно признаку Даламбера радиус сходимости степенного ряда определяется как 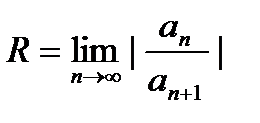, а согласно признаку Коши - R = 1/.

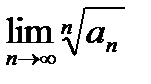@ Задача 1. Найти радиус сходимости степенного ряда .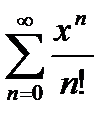

Решение: Радиус сходимости можно найти по формуле Даламбера

= .

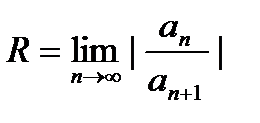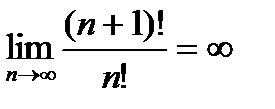Следовательно, степенной ряд абсолютно сходится на всей числовой оси.

@ Задача 2. Найти радиус сходимости степенного ряда .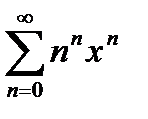

Решение: Радиус сходимости находим по формуле Коши

R = 1/= .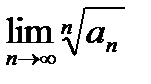

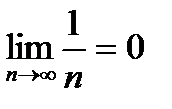Следовательно, степенной ряд сходится лишь в одной точке x₀ = 0.