Предел последовательности и его свойства
Функция называется целочисленной или последовательностью, если область определения функции представляет собой множество натуральных чисел.
þ Обозначения: Последовательности обозначаются как {an}, {yn}, члены последовательности как – an, yn.
Число b называется пределом последовательности {yn}, если по мере возрастания n член yn неограниченно приближается к значению b:
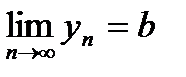 .
. 
Символ lim от латинского слово «limes» - предел; символ n ® ¥ подчеркивает, что n неограниченно возрастает («стремится к бесконечности»).
! Примеры: Члены последовательности 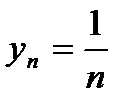 по мере возрастания n стремятся к нулю: y1 = 1; y2 = 0,5; y3 = 0,33¼; y4 = 0,25; ¼; y100 = 0,01; ¼; y1000 = 0,001; ¼ Следовательно, пределом последовательности является число 0:
по мере возрастания n стремятся к нулю: y1 = 1; y2 = 0,5; y3 = 0,33¼; y4 = 0,25; ¼; y100 = 0,01; ¼; y1000 = 0,001; ¼ Следовательно, пределом последовательности является число 0:
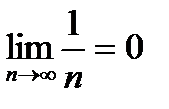 . (1)
. (1)
! Пример: Члены последовательности 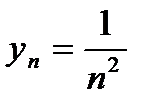 по мере возрастания n стремятся к нулю, поэтому
по мере возрастания n стремятся к нулю, поэтому 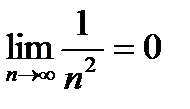 . (2)
. (2)
! Пример: Предел постоянной величины c равен самой постоянной величине c (3).
Более строгое определение предела следующее.
Число b называется пределом последовательности {yn}, если абсолютная величина разности yn – b, начиная с некоторого номера N, остается меньшей любого заранее данного положительного числа e: |yn – b| < e при n ³ N (N зависит от величины e).
Последовательность, имеющая предел, называется сходящейся, в противном случае, она расходящаяся.
Свойства пределов
1. Постоянный множитель можно вынести за знак предела: 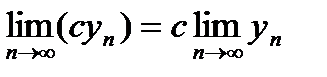 .
.
2. Предел суммы (разности) равен сумме (разности) пределов: 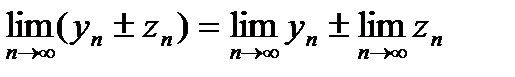 .
.
3. Предел произведения равен произведению пределов: 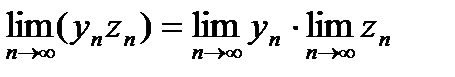 .
.
4. Предел отношения равен отношению пределов: 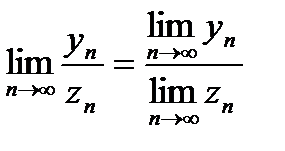 , если
, если 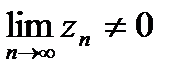 .
.
Эти свойства справедливы не только для последовательностей, но и для функций y(x).
@ Задача 1. Найти предел последовательности 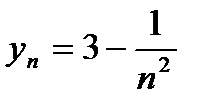 .
.
Решение: Предел последовательности находится, применяя второе свойство пределов и частные пределы (2) и (3):
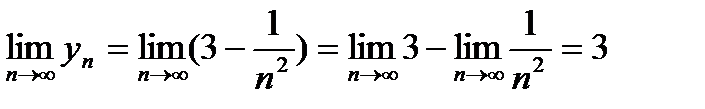 .
.
Дата добавления: 2016-06-15; просмотров: 2203;











