Граничное условие первого рода.

Определяет температуру на поверхности тела в любой момент времени, то есть

T_s = T_s (x, y, z, t) (2.15)

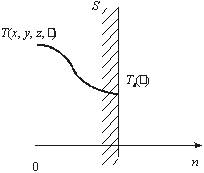
Рис. 2.4 – Изотермическое граничное условие.

Как бы не изменялась температура внутри тела, температура точек на поверхности подчиняется уравнению (2.15).

Кривая распределения температуры в теле (рис. 2.4) на границе тела имеет заданную ординату T_s, которая может изменяться во времени. Частным случаем граничного условия первого рода является изотермическоеграничное условие, при котором температура поверхности тела остается в течение всего процесса теплопередачи постоянной:

T_s = const.

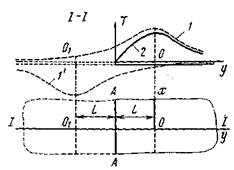
Рис. 2.5 – Условие первого рода

Чтобы представить себе такое состояние тела необходимо предположить, что симметрично источнику тепла, действующему в теле, действует другой, фиктивный источник тепла вне его с отрицательным знаком (так называемый сток тепла). Причем свойства этого стока теплоты в точности совпадают со свойствами действительного источника тепла, а распределение температур описывается одинаковым математическим выражением. Суммарное действие этих источников приведет к тому, что на поверхности тела установится постоянная температура, в частном случае Т = 0 8С, в то время как в пределах тела температура точек непрерывно меняется.

Граничное условие второго рода

Определяет плотность теплового потока в любой точке поверхности тела в любой момент времени, т.е.

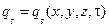
По закону Фурье плотность теплового потока прямо пропорциональна градиенту температуры. Поэтому температурное поле на границе имеет заданный градиент 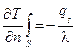(рис. б), в частном случае постоянные, когда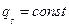

Частным случаем граничного условия второго рода является адиабатическое граничное условие, когда тепловой поток через поверхность тела равен нулю (рис. 2.6), т.е.

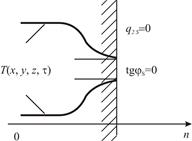
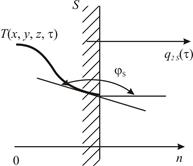
Рис. 2.6 - Граничное условие второго рода

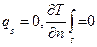
В технических расчетах часто встречаются случаи, когда тепловой поток с поверхности тела мал по сравнению с потоками внутри тела. Тогда можно принять эту границу как адиабатическую. При сварке такой случай может быть представлен следующей схемой (Рис. 2.7).

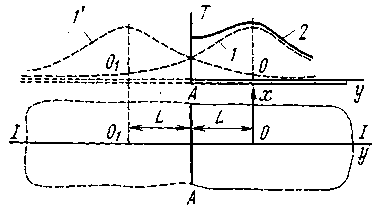
Рис. 2.7 – Условие второго рода

В точке О действует источник тепла. Чтобы выполнить условие – граница не пропускает тепло, необходимо симметрично этому источнику поместить такой же источник вне тела, в точке О₁, причем тепловой поток от него направлен против потока основного источника. Они взаимно уничтожаются, то есть граница тепла не пропускает. Однако температура края тела окажется вдвое больше, если бы это тело было бесконечным. Этот прием компенсации теплового потока носит название метода отражения, так как в этом случае теплонепроницаемая граница, может рассматриваться как граница, отражающая тепловой поток, идущий со стороны металла.

Граничное условие третьего рода.

Определяет температуру окружающей среды и закон теплообмена между поверхностью тела и окружающей средой. Наиболее простую форму граничного условия третьего рода получим, если теплообмен на границе зададим уравнение Ньютона, которое выражает, что плотность теплового потока теплоотдачи 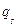через граничную поверхность прямо пропорциональную разности температур граничной поверхности 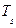и окружающей среды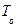

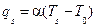
Плотность теплового потока, подтекающая к граничной поверхности со стороны тела, по закону Фурье прямо пропорционально градиенту температуры на граничной поверхности:

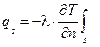
Приравнивая поток теплоты, поступающей со стороны тела, к потоку теплоотдачи, получаем граничное условие 3-го рода:

,

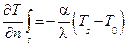выражающее, что градиент температуры на граничной поверхности прямо пропорционален перепаду температуры между поверхностью тела и окружающей средой. Это условие требует, чтобы касательная к кривой распределения температуры в граничной точке переходит через направляющую точку О с температурой 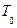, находящуюся вне тела на расстоянии 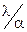от граничной поверхности (рис. 2.8).

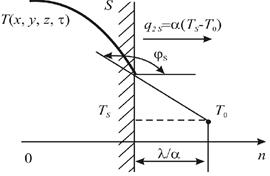
Рисунок 2.8 – Граничное условие 3 рода

Из граничного условия 3-го рода можно получить как частный случай изотермическое граничное условие. Если 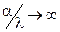, что имеет место при очень большом коэффициенте теплоотдачи 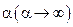или очень малом коэффициенте теплопроводности 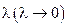, то:

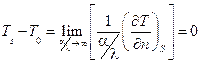
и 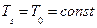, т.е. температура поверхности тела постоянна в течение всего процесса теплообмена и равна температуре окружающей среды.

Адиабатическое граничное условие также можно получить как частный случай граничного условия 3-го рода.

Действительно, при 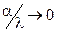, что имеет место при малом 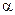и большом 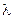, получим 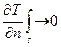, т.е. тепловой поток через граничную поверхность очень мал.

Граничное условие четвертого рода

Характеризует теплообмен системы тел или тела с окружающей средой по закону теплопроводности. При наличии между телами совершенного теплового контакта температуры соприкасающихся поверхностей одинаковы, т.е.

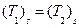
Кроме того, в рассматриваемых условиях имеет место равенство тепловых потоков, проходящих через граничную поверхность, т.е.

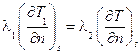
Граничное условие 4-го рода требует, чтобы отношение тангенсов угла наклона касательных к температурным кривым в точке соприкосновения тел было постоянным (рис. 2.9)

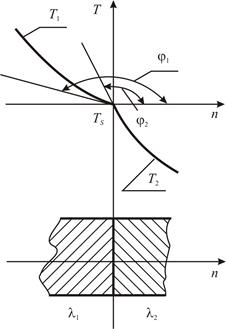
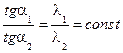
Рисунок 2.9 - Граничное условие 4-го рода