Векторное произведение двух векторов, его свойства. Условие параллельности двух векторов
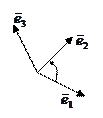 Определение. Упорядоченная тройка векторов
Определение. Упорядоченная тройка векторов 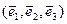 называется право ориентированной, если с конца вектора
называется право ориентированной, если с конца вектора 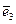 кратчайший поворот от вектора
кратчайший поворот от вектора 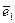 к
к 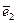 виден совершающимся против хода часовой стрелки, и лево ориентированной, если по часовой:
виден совершающимся против хода часовой стрелки, и лево ориентированной, если по часовой:
Определение. Векторным произведением векторов  и
и 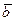 в Е3 называется вектор
в Е3 называется вектор 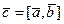 ,
, 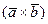 ,
, 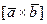 , удовлетворяющий условиям:
, удовлетворяющий условиям:
1) 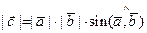 .
.
2) 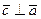 ,
, 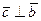 ,
,
3) векторы  ,
, 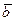 ,
, 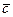 образуют правую тройку векторов.
образуют правую тройку векторов.
Ясно, что 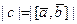 численно равен площади Sÿ
численно равен площади Sÿ 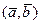 параллелограмма, построенного на векторах
параллелограмма, построенного на векторах  и
и 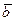 , как на сторонах.
, как на сторонах.
 |
Свойства векторного произведения:
1°. 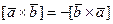 .
.
2°. 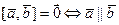 .
.
3°. 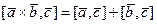 .
.
4°. 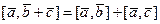 . (26)
. (26)
5°. 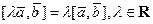 .
.
6°. 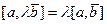 .
.
7°. 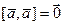 .
.
Эти свойства следуют из определения векторного произведения.
Составим таблицу векторного умножения ортов 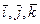 :
:
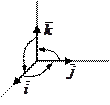
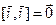 ,
, 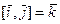 ,
, 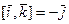 ,
,
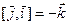 ,
, 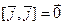 ,
, 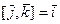 , (27)
, (27)
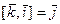 ,
, 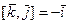 ,
, 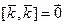
Пусть даны два вектора
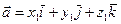 и
и 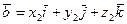 .
.
Пользуясь свойствами (26) векторного произведения и таблицей (27), найдем векторное произведение 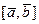 , перемножая их как многочлены:
, перемножая их как многочлены:
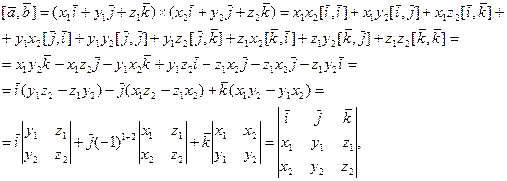
т.е. имеем
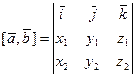 (28)
(28)
- запись векторного произведения в форме определителя третьего порядка.
 Пусть в прямоугольной д.с.к.
Пусть в прямоугольной д.с.к. 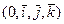 даны три точки
даны три точки 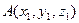 ,
, 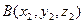 и
и 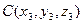 . Найдем SÿАВСД и SDАВС.
. Найдем SÿАВСД и SDАВС.
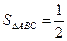 SÿАВСД, но
SÿАВСД, но
SÿАВСД = 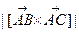 . (29)
. (29)
Поэтому
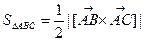 . (30)
. (30)
Имеем
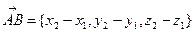 ,
,
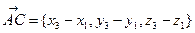 .
.
Отсюда и из (28) будем иметь
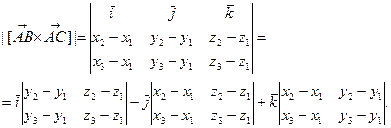
Следовательно,
SÿАВСД = 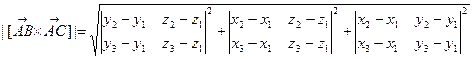
§ 4. Смешанное произведение векторов, его свойства. Объем параллелепипеда и пирамиды. Условие компланарности трех векторов.
Определение. Смешанным произведением трех векторов  ,
, 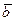 ,
, 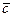 называется число
называется число 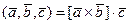 .
.
Здесь векторы  и
и 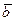 перемножаются векторно, а их результат скалярно на третий вектор
перемножаются векторно, а их результат скалярно на третий вектор 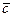 . Поэтому смешанное произведение называют еще векторно-скалярным.
. Поэтому смешанное произведение называют еще векторно-скалярным.
 Построим параллелепипед на векторах
Построим параллелепипед на векторах  ,
, 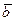 ,
, 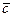 и вектор
и вектор 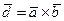 ,
, 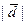 =Sÿ
=Sÿ 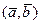 . Имеем
. Имеем 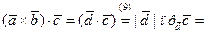 Sÿ
Sÿ 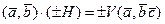 , где
, где 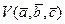 - объем параллелепипеда, образованного векторами
- объем параллелепипеда, образованного векторами  ,
, 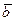 ,
, 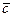 , который берется со знаком +, если векторы
, который берется со знаком +, если векторы  ,
, 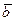 ,
, 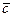 образуют правую тройку векторов, и со знаком -1, если они образуют левую тройку векторов. Во всех случаях
образуют правую тройку векторов, и со знаком -1, если они образуют левую тройку векторов. Во всех случаях
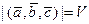 . (31)
. (31)
Если векторы  ,
, 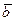 ,
, 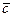 компланарны, то
компланарны, то 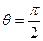 , и поэтому
, и поэтому 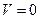 . Отсюда и из (31) получаем
. Отсюда и из (31) получаем
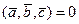 (32)
(32)
- условие компланарности трех векторов.
Пусть в прямоугольной д.с.к. 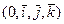 даны векторы
даны векторы  ,
, 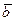 и
и 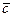 :
:
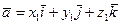 ,
,
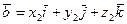 ,
,
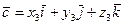 .
.
Найдем их смешанное произведение, используя формулы (28) для векторного и (18) скалярного произведений векторов:
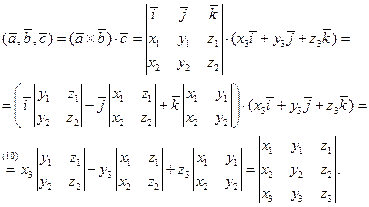
Таким образом,
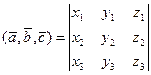 . (33)
. (33)
Из (33) и свойств определителя получаем свойства смешанного произведения:
1) 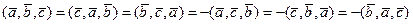 ;
;
2) 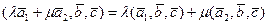 .
.
Из (32) и (33) получаем условие компланарности трех векторов в координатной форме
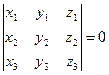 . (34)
. (34)
На основании (33) находим формулу для вычисления объёма пирамиды
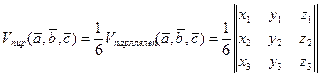 .
.
Дата добавления: 2016-11-04; просмотров: 2545;











