Рівняння руху механізму

<16 17 181920 21 22 >

При вивченні руху механізму ми звичайно припускали, що початкова ланка (головний вал машини) обертається із сталою швидкістю (w₁=const). Цей закон руху можна одержати в тих випадках, коли структура механізму проста, наприклад у механізмах, що складаються тільки з обертових ланок. Для здійснення такого руху потрібні цілком певні співвідношення між силами, що діють на механізм, і масами його ланок. Але закон зміни сил залежить від їх фізичної природи й до структури механізму відношення не має. Тому взагалі кажучи, не можна встановити між силами, що діють на механізм, таке співвідношення, яке б забезпечило заданий закон його руху.

Закон руху будь-якої ланки механізму може бути визначений лише тоді, коли відомі всі зовнішні сили або залежність цих сил від різних параметрів. Як було вказано раніше (п.4.2) рушійні сили й сили виробничих опорів можуть залежати одночасно або окремо від положення ланки, яка прийнята за початкову, або. від її кутової швидкості. Зведені моменти інерції J_ЗВ механізму чи машини можуть бути або сталими, або залежати від положень початкової ланки (п. 4.7).

Визначення закону руху механізму, що перебуває під дією прикладених до його ланок сил, і є задачею динамічного аналізу. Для механізму, що має один ступінь вільності, цю задачу можна вважати розв'язаною, коли буде встановлено закон руху однієї ланки. Звичайно за таку ланку обирають вхідний вал робочої машини або вихідний вал двигуна До цієї ланки, що приймається за ланку зведення, доцільно звести всі сили й моменти пар сил, прикладені до механізму, та маси й моменти інерції його ланок. Тоді замість розгляду всього комплексу сил, що діють на ланки механізму, можна розглянути сили, що діють лише на одну ланку - ланку зведення, наприклад кривошип ОА (рис. 4.11), що перебуватиме під дією зведеної

сили F_зв або зведеного моменту М_зв (у загальному випадку змінних) і матиме зведену масу m_зв, зосереджену ніби в точці А зведення, або зведений момент інерції J_зв всіх ланок, який наданий ланці зведеня ОА . Закон руху всіх інших ланок механізму можна визначити, якщо відомий закон руху початкової ланки.

Для розв'язання цієї задачі динаміки (знаходження закону руху початкової ланки механізму) використовують рівняння руху, яке може бути записане в енергетичній або диференціальній формі.

Основою для складання рівняння руху механізму служить теорема про зміну кінетичної енергії, згідно з якою зміна кінетичної енергії механічної системи за будь-який проміжок часу дорівнює сумі робіт усіх прикладених сил, що діють на цю систему на протязі цього ліс проміжку часу, тобто

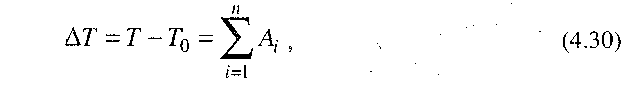
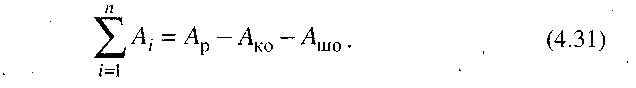
Крім цього, якщо звести всі сили й маси до вибраної ланки зведення, рівняння (4.30) з урахуванням (4.31) можна записати так:

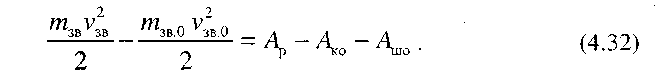
При обертовому русі ланки зведення рівняння (4.32) можна записати у такому вигляді:

де Jзв, J_ЗВ.0- зведені моменти інерції механізму; w, w₀ - кутові швидкості ланки зведення відповідно в кінці і на початку проміжку часу який ми розглядаємо.

Теорема про зміну кінетичної енергії записана у вигляді рівнянь (4.32) або (4.33) носить назву рівняння руху механізму в енергетичній формі(у формі інтеграла енергії).

Враховуючи, що роботу зведених рушійних сил і сил опору можна виразити через зведений момент М_зв = М_р + М₀ рушійних сил і сил опору, який прикладаємо до ланки зведення,

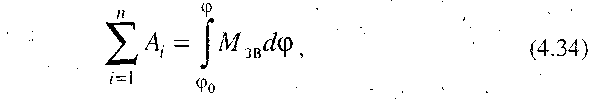
рівняння (4.33) набуває вигляду

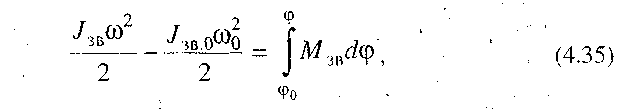
де 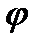- узагальнена координата (кут повороту ланки зведення); 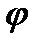₀ - значення кута 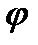на початку руху.

Рівняння руху механізму може також бути записано в диференціальній формі, яке можна дістати з рівняння кінетичної енергії в диференціальній формі:

При обертовому русі початкової ланки після зведення сил і мас маємо

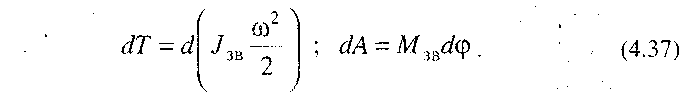
Підставляючи (4.37) у рівняння (4.36), можна записати

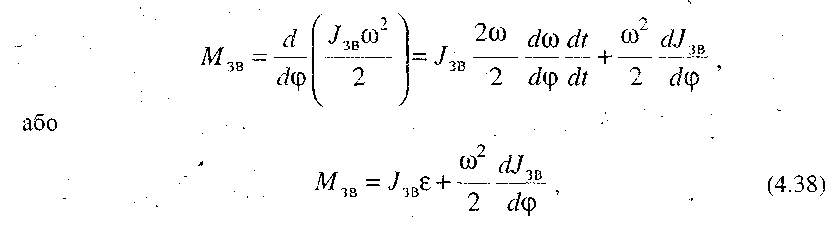
де 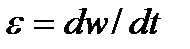- кутове прискорення ланки зведення; 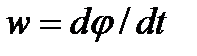- кутова швидкість цієї ланки.

Такий самий вигляд має диференціальне рівняння руху механізму при прямолінійному русі початкової ланки:

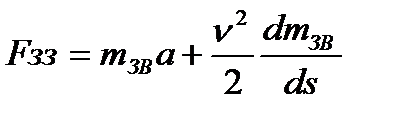(4.39)

де s, 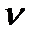,а - відповідно переміщення, швидкості і прискорення ланки зведення; F_ЗВ,m_ЗВ зведені сили і маси механізму.

<16 17 181920 21 22 >

Дата добавления: 2016-06-15; просмотров: 2126;