ВИЗНАЧЕННЯ ПОЛОЖЕНЬ ЛАНОК ГРУП І ПОБУДОВА ТРАЄКТОРІЙ, ОПИСУВАНИХ ТОЧКАМИ ЛАНОК МЕХАНІЗМУ.

Для вирішення задачі про положення ланок механізму (плану механізму) повинні бути задана кінематична схема механізму (КСМ) і функція переміщень початкової ланки (для w=1) чи функції переміщень початкових ланок для механізмів з декількома ступенями вільності.

Для визначення положень ланок механізму у визначеному масштабі будують його КСМ (план механізму).

Розглянемо графічний метод на прикладі шестиланкового важільного механізму маніпулятора подачі заготовок (рис.3). Ланка 1 (кривошип) обертається з постійною кутовою швидкістю ω. При побудові плану механізму кут повороту ланки 1, що є узагальненою координатою, розділимо на ряд послідовних кутових кроків, рівних між собою (наприклад, на 12 кутових кроків, кожний з який дорівнює 30˚ ).

За нульове положення ланки 1 виберемо його положення відповідне крайньому лівому положенню вихідної ланки 5 (повзун). При цьому ланка 1 і ланка 2 (шатун) повинні бути розташовані на одній прямій(точка A праворуч від точки O₁ ).

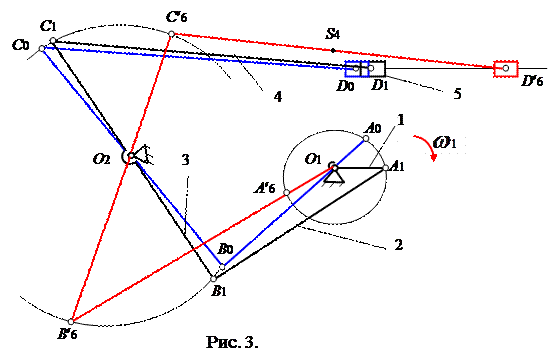Точка А описує коло радіусу О₁А , послідовні положення якої відзначені арабськими цифрами 1, 2, 3,..., 12. Для визначення положень ланок 2 і 3 досить знайти положення кінематичної пари В, шарнірно з'єднуючі ці ланки між собою.

Точка В описує дугову траєкторію радіуса А₂В В в її відносному русі навколо точки О₂ і дугову траєкторію радіуса BА в її русі відносноточки А. Точка перетину цих двох дугових траєкторій знаходиться задопомогою циркуля. Подібну побудову називають способом засічок.

Для інших положень вхідної ланки 1 виконують аналогічні побудови і знаходять послідовні положення точки В на колі радіусу О₂В, що розташовані нерівномірно.

Для визначення положень ланок 4 і 5 досить знайти положення точки D. Траєкторією точки D відносно стояка 6 є пряма x - x, а траєкторією цієї ж точки відносно точки C ланки 3 є дуга радіуса CD. Точка перетинання цих двох траєкторій і визначає для кожного положення точку D.

На плані механізму в разі потреби можна побудувати траєкторії, описувані будь-якою точкою тієї чи іншої ланки, положення якої вже знайдено, наприклад точки S₄ центра мас ланки 4. Подібні траєкторії точок, розташованих на ланках, що здійснюють плоскопаралельний рух, називають шатунними кривими.

6.5. ПОБУДОВА ДІАГРАМ ПЕРЕМІЩЕННЯ

При дослідженні механізмів часто недостатньо знати лише форму шляху – траєкторію руху точки; потрібно ще знати характер зміни довжини пройденого шляху залежно від часу чи кута повороту кривошипа (узагальненої координати). Для цього будують діаграми лінійних s=s(t), або кутових β=β(t) переміщень.

Розглянемо побудову діаграми переміщень повзуна Вдля кривошипно-повзункового механізму (рис. 4).

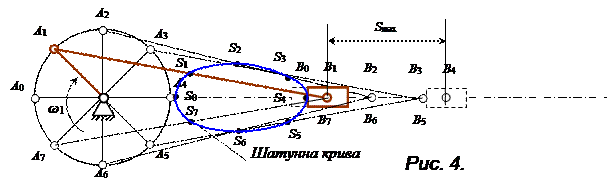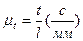За умови рівномірного обертання початкової ланки (ω₁=const) через рівні проміжки часу кривошип повертатиметься на однакові кути, а переміщення повзуна будуть вимірюватись відрізками В₀В_1, В₀В_{2 . .}_.і т.д._,Далі будують прямокутну систему координат S – t: по осі ординат – переміщення S , по осі абсцис – час t. На осі абсцисвідкладають відрізок l = (0 - 0), який зображує у масштабі , період Т, с, одного обороту кривошипа ОА (або кут 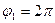); на осіординат — лінійні переміщення повзуна В у масштабі 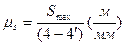, де S_max— максимальний хід повзуна В, м; (4-4΄) — відрізок, мм,на діаграмі, який зображує цей хід.

Відрізок l ділять на таку кількість відрізків 0—1, 1—2,..., 7–0, на яку розбита траєкторія точки А (уданому випадку на 8). Точки О,І, 2,... відповідають моментам часу, коли механізм займатиме відповідно положення О, І, 2,... Тоді на ординатах відкладають у вибраному масштабі 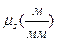, переміщення точки В від крайнього положення В₀ за певні проміжки часу. Якщо масштаби довжини (рис. 3.1) і переміщень (рис. 3.4) рівні, то відрізки1—1΄, 2—2', ... на діаграмі будуть відповідно рівні відрізкам B₀B₁ В₀В₂,... на плані механізму. Одержані точки 0, 1΄, 2' з'єднують плавною кривою, яка і буде діаграмою переміщень повзуна В: s = s(t).

3.3. Дослідження руху механізмів методом кінематичних діаграм

Маючи діаграму (графік) переміщеня, будь-якої точки або ланки механізму як функцію шляху s залежно від чаcу t, методом графічного диференціювання можна визначити швидкості і прискорення точки (ланки), рух якої визначають.

Для побудови діаграми швидкостей v=v(t) використовують залежність

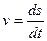. (6)

Як відомо, похідна функції s = s(t) у точці А (рис. 3.5) визначається тангенсом кута нахилу дотичної до цієї кривої s = s(t), проведеної через точку А. З урахуванням масштабів побудови діаграми s = s(t) можна записати

ds=∆yμ_s, dt=∆xμ_l

Тоді залежність (3.2) набуде вигляду

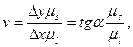(7)

де α — кут нахилу дотичної у точці А діаграми s = s(t);μ_s, μ_t – масштаби діаграми по осях ординат і абсцис відповідно.

Із залежності (7) видно, що швидкість руху точки в будь-якому положенні пропорційно зв'язана з тангенсом кута нахилу дотичної, оскільки масштаби μ_s і μ_t , є величинами сталими.

Таким чином, щоб побудувати діаграму швидкостей v=v(t). беруть ряд точок на діаграмі s = s(i) і через них проводять дотичні. Знайшовши тангенс кутів нахилу цих дотичних у відповідних положеннях, будують діаграму tg α_і=f(t). Ця діаграма одночасно буде діаграмою швидкостей у деякому масштабі, який можна знайти, використовуючи залежність (7).

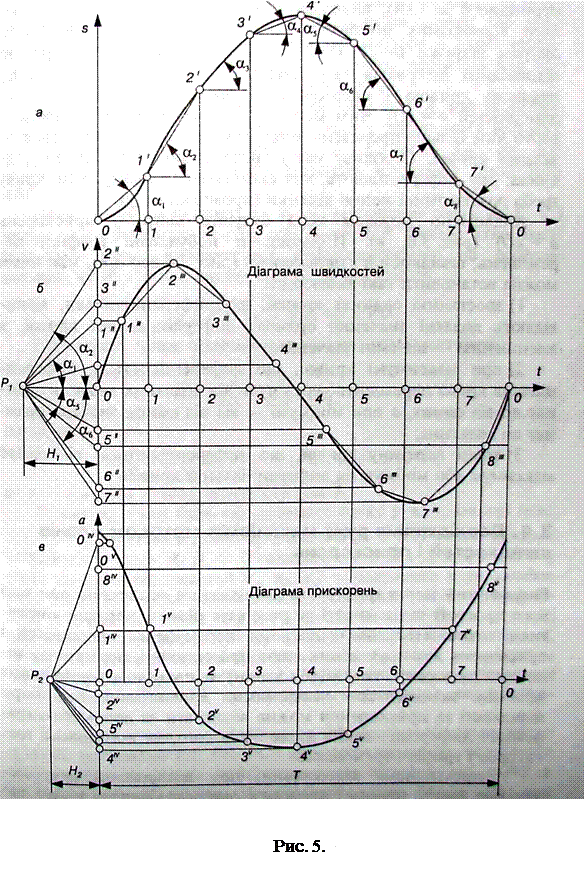
На практиці для побудови діаграм швидкостей і прискорень використовують два методи — метод дотичних і метод хорд.

На рис. 5 показані кінематичні діаграми (переміщення, швидкість і прискорення точки В, які побудовані методом хорд.

Дата добавления: 2016-06-15; просмотров: 2422;

Поиск по сайту

Узнать еще