ВИЗНАЧЕННЯ ЗВЕДЕНОГО МОМЕНТУ ІНЕРЦІЇ МЕХАНІЗМУ.

в)

б)

а)

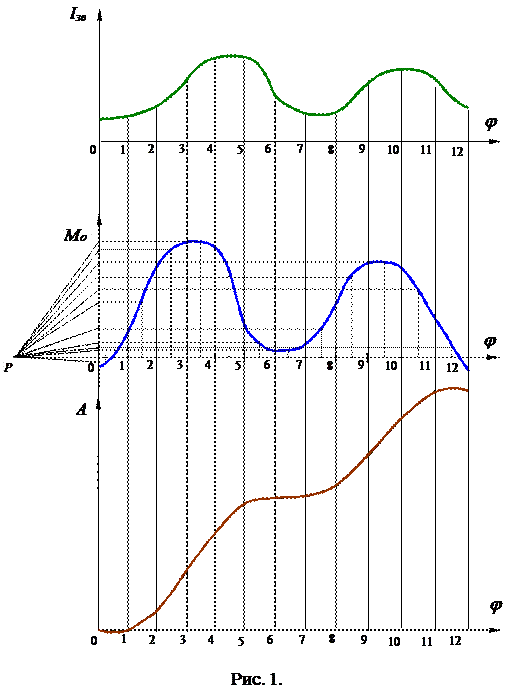Для досліджуваних n положень механізму за формулою (1) визначаємо зведений до початкової ланки момент інерції механізму і будуємо його діаграму (рис.1 а).

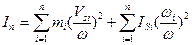(1)

1.2.2. ВИЗНАЧЕННЯ ЗВЕДЕНОГО ДО ПОЧАТКОВОЇ

ЛАНКИ МОМЕНТУ СИЛ ОПОРІВ

Для n положень механізму визначаємо зведений до початкової ланки моментів сил опору :

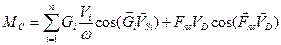(2)

За розрахунковим значенням приведених моментів будуємо відповідний графік, для зручності побудов негативні значення моментів відкладаємо вище осі абсцис (рис.1 б).

1.2.3. ПОБУДОВА ГРАФІКА РОБОТИ СИЛ ОПОРІВ

Графічно інтегруємо графік моментів сил опорів, у результаті отримуємо графік робіт сил опорів (рис.1 в).

Масштабний коефіцієнт графіка робіт визначаємо за формулою:

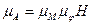, (3)

де 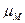= 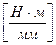- масштабний коефіцієнт діаграми моментів сил опорів;

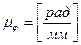- масштабний коефіцієнт кутової координати ланки зведення

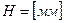- полюсна відстань.

Масштабний коефіцієнт кутової координати початкової ланки визначаємо за формулою:

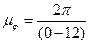, (4)

де (0-12) відстань від початкової точки (0) осі абсцис до її кінцевої точки (12), (мм).

1.2.4. ВИЗНАЧЕННЯ НЕОБХІДНОЇ ПОТУЖНОСТІ ПРИВОДА

Необхідну потужність двигуна визначаємо за формулою:

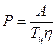, (5)

де А - робота сил опорів за цикл сталого руху:

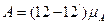; (6)

Т_Ц – час циклу (час одного оберту початкової ланки), визначаємо за формулою:

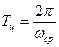, (7)

де, w_ср – середня кутова швидкість початкової ланки:

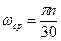; (8)

h - коефіцієнт корисної дії (к.к.д) машини:

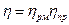, (9)

де h_рм - к.к.д. підйомного механізму, приймає такі значення:

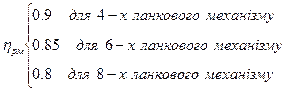
h_пр – к.к.д приводу, для механізму маніпулятора, розроблювального в курсовому проектуванні, визначаємо за формулою:

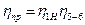, (10)

де 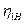- к.к.д. планетарного редуктора;

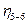- к.к.д. пари зубчастих коліс 5,6, для пари зубчастих коліс зовнішнього зачеплення 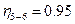; для пари коліс внутрішнього зачеплення .

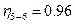1.2.5. ПОБУДОВА МЕХАНІЧНОЇ ХАРАКТЕРИСТИКИ АСИНХРОННОГО ЕЛЕКТРОДВИГУНА З КОРОТКОЗАМКНЕНИМ РОТОРОМ

Механічна характеристика показує залежність частоти обертання від рушійного моменту на валу двигуна (рис. 2).

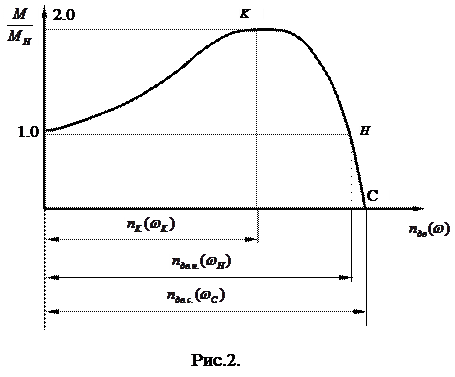Позначимо робочу ділянку характеристики (Н, С) обмежену робочою точкою Н номінального режиму й т. С відповідній синхронній частоті магнітного поля статора.

Номінальний режим відповідає паспортним даним електродвигуна. Тому момент номінальний двигуна визначаємо за формулою:

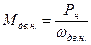(11)

де Р_Н – номінальна (паспортна потужність двигуна, Вт);

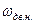- номінальна кутова швидкість ротору двигуна, .

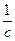Механічну характеристику приведемо до початкової ланки механізму, у цьому випадку це залежність .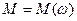

Номінальний момент зведений до початкової ланки:

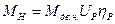. (12)

Номінальна кутова швидкість початкової ланки:

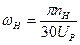. (13)

Синхронна кутова швидкість початкової ланки

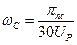, (14)

де 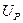- передатне відношення між двигуном та початковою ланкою.

На ділянці (Н,С) механічну характеристику можна апроксимувати параболічною залежністю виду

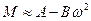, (15)

де А, В - коефіцієнти, які визначаються з умови, що апроксимуюча парабола проходить через точки Н, С з координатами .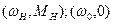

Тоді щоб визначити А і В необхідно записати рівняння:

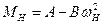; (16)

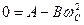, (17)

звідки

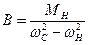; (18)

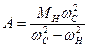. (19)

Розділимо цикловий кут повороту початкової ланки (у більшості випадків 2p) на n рівних частин і позначимо відповідні вузлові точки на кривій зведеного моменту сил опору 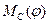та кривої зведеного моменту інерції агрегату 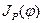. Остання функція містить змінну і постійну складові.

Перша зумовлена наявністю виконавчого шарнірноважільного механізму, друга - зведений момент інерції ротора двигуна і редуктора.

Зведений момент інерції ротора двигуна дорівнює:

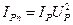. (20)

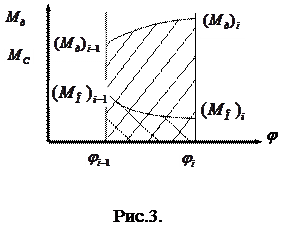
Розглянемо два положення механізму з номерами і-1 , і, які відповідають повороту початкової ланки від j_i-1 до j_і (рис.3).

Робота рушійних сил на цьому відрізку

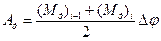. (21)

Використовуючи залежність (21) запишемо

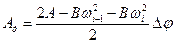. (22)

З таким же наближенням визначається робота сил опору

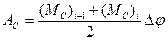. (23)

Застосовуючи теорему про зміну кінетичної енергії маємо для

відрізка :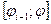

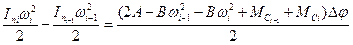. (14)

Це рівняння зв'язує значення кутової швидкості наприкінці відрізка і на його початку.

Розв’язавши його відносно 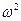визначимо:

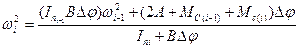. (15)

Змінюючи значення і від і=1 до n можливо крок за кроком отримати значення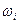

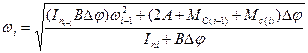. (16)

Відкритим поки залишається питання про початкове значення .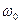

Задамо орієнтовно значення 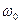(в межах робочої ділянки характеристики) і розрахуємо значення 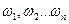. Внаслідок наближеного значення 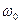можливо що 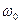не дорівнює 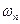тобто умова періодичності не виконується.

Далі виконаємо розрахунок для наступного циклу, але тепер за 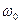приймаємо значення 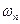знайдене наприкінці першого оберту. Цей процес будемо продовжувати поки 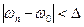, де 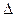- припустима погрішність у визначенні періодичного руху.

Завдяки тому, що асинхронні двигуни мають здатність саморегулювання, буває досить виконати розрахунок для декількох обертів початкової ланки.

Після того як усталений рух знайдений, можна визначити коефіцієнт нерівномірності і порівняти його з припустимим значенням. Якщо 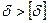то необхідно визначити момент інерції маховика, що забезпечить зниження 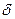до припустимого рівня.

Приймаючи приблизно, що 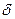обернено пропорційний постійній складовій I₀ зведеного моменту інерції машинного агрегату, маємо, що необхідне збільшення до моменту інерції:

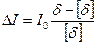(17)

Так як ця формула є наближеною, буде потрібно декілька спробних розрахунків поки не виявиться, що в результаті знайдений момент 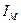, що забезпечить нерівномірність обертання меншу допустимої.

Після цього необхідно також перевірити, чи не виходить значення 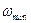за межі відрізка 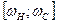де агрегат працює без перевантаження. Якщо буде ділянка де двигун перевантажений 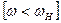необхідно вибрати двигун більшої потужності.

Нижче приводимо програму визначення реальної кутової швидкості початкової ланки і моменту інерції маховика, оформлену у вигляді модуля.

У програмі прийняті наступні ідентифікатори:

DD - припустиме значення коефіцієнта нерівномірності руху;

N - кількість положень;

DF - збільшення кута повороту початкової ланки;

Мрс[і] - зведений момент опору;

Ipr[і] - зведений момент інерції рухливих ланок;

w[і] - кутова швидкість початкової ланки;

МN - номінальний момент приводного електродвигуна;

NC - синхронна частота обертання асинхронного

електродвигуна;

NDN - номінальна частота обертання двигуна;

UR - передаточне число редуктора;

OH - номінальна кутова швидкість початкової ланки;

ОС - синхронна кутова швидкість початкової ланки;

А,У - коефіцієнти;

D - коефіцієнт нерівномірності обертання початкового

ланки;

DI - збільшення моменту інерції маховика;

IM - момент інерції маховика.

Перерахунок Іі

Обч. ωmax ωmin

ω0=ωн

i=i+1

ωi=F(ωi-1)

i=1

ω0=ωн

Вивід ωі ,Ім

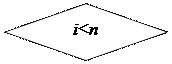
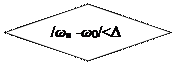
Program P1;

Const

N=12;

Mc(n), I(n), Mн,nc, nн, Iн=0

VAR i:integer;

w,H,{Ipr,}Mnc,Mnco:array [0..N] of real;

A,B,DD,DF,IM,wH,wC,wM,w1:real;

D,Di:real;

MDn,nDC,nDn,UR:real;

label 1,2;

begin

for i:=0 to N do

Mnco[i]:=Mnc[i];

end;

DF:=2*PI/(N);

IM:=0;

wH:=PI*nDn/(30*UR);

wC:=PI*nDC/(30*UR);

w[0]:=wH;

MDn:=MDn*UR;

B:=MDn/(SQR(w)-SQR(w));

A:=B*SQR(w);

1: і:=0; { Мітка 1 }

FOR I:=1 TO N do

begin

w[I]:=SQRT(((Ipr[I-1]-DF*B)*SQR(w[I-1])+(2*A+Mnco[I-1]+Mnco[I])*

DF)/(Ipr[I]+B*DF));

end;

IF (ABS(w[N]-w[0]))>0.1 THEN

begin

w[0]:= w[N]; GOTO 1;

end;

for i:=0 to N do

begin

H[i]:=30*w[i]*UR/PI; writeln(w[i]:7:3,' ',H[i]:7:3);

end;

wM:=w[0];w1:=w[0];

FOR I:= 1 TO N

do

begin

IF w[I]>wM THEN wM:= w[I]; IF w[I]<w1 THEN w1:= w[I];

end;

D:=(wM - w1)/wH;

IF D<DD THEN goto 2;

DI:=5; IM:=IM+DI; write('D=',D,'DI=',DI,'IM=',IM);

FOR I:= 0 TO N do

Ipr[I]:=Ipr[I]+DI; w[0]:=wH;

GOTO 1;

2: IF (w1*1000)<(wH*1000) THEN writeln('w1 < wH');

FOR I:=0 TO N

do

H[i]:=30*w[i]*UR/PI;

writeln('w[',I,']=',w[I],' H[',i,']=',H[i]);

writeln('DD=',DD:4:3,' IM=',IM:5:3);

write;

WRITE('w1=',w1,' wH=',wH,' wM=',wM);

WRITE(F1,' ');

WRITE(F1,' ');

WRITE(F1,' Вихідні дані і результати виконання програми: ');

WRITE(F1,'DD=',DD:4:3,' N=', N,' MDn=',MDn/ur:4:3,' Н*м nDc=',

nDc:3:0,' 1/хв');

WRITE(F1,'nDn=',nDn:3:0,'1/хв UR=',UR:5:2,'IM=',IM:5:2,' кг*м^2');

END.