Силовий розрахунок плоских механізмів без урахування сил тертя

Основні задачі силового розрахунку. Визначення сил, що діють на ланки механізмів, має велике практичне значення для розрахунків ланок на міцність, жорсткість, вібростійкість, зносостійкість, довговічність, для визначення втрат енергії на тертя, а також для підрахунку енергетичного балансу машини та виконання інших подібних розрахунків.

Основними задачами силового розрахунку механізмів є, по-перше, визначення зовнішніх невідомих сил, що діють на ланки механізмів; по-друге, визначення сил взаємодії ланок у місцях їх стикання, тобто реакцій у кінематичних парах; по-третє, визначення зрівноважувальної сили або зрівноважувального моменту сил.

При розв'язуванні задач силового розрахунку механізмів припус­кається, що закон руху початкової ланки задано; так само припускається, що маси і моменти інерції ланок відомі. Отже, завжди можна визначити ті сили інерції, які необхідні для розв'язання задач силового розрахунку. У першому наближенні силовий розрахунок проводять без урахування сил тертя в кінематичних парах.

Найпростішим випадком силового розрахунку механізмів є рівновага, тобто коли ланки механізму перебувають у стані спокою або рівномірному пря­молінійному русі. У цих випадках не виникають динамічні сили (сили інерції). Тому для розв'язання такої задачі досить звичайних рівнянь статики У загально­му випадку, при наявності прискорень, виникають сили інерції, і рівнянь статики тут мало. Щоб розв'язати задачу про знаходження сил, використовують принцип Даламбера, згідно з яким рухома система тіл перебуває у кожний момент часу в рівновазі під дією зовнішніх сил, включаючи сили інерції

Таким чином, користуючись принципом Даламбера, можна задачу динаміки розв'язати методами статики, якщо умовно віднести до зовнішніх сил і сили (моменти сил) інерції, які виникають при русі ланок з прискоренням і діють на елементи кінематичних пар як додаткові сили Проте треба пам'ятати, що сили інерції, які докладаємо до ланок, умовні. Вони діють на іншу ланку, яка спричиняє прискорений рук даної ланки. У такому змісті і ро­зуміють характер сил інерції.

Розв'язання задачі динаміки методами статики називають кінетостатичнимрозрахунком.

Статична визначеність структурної групи. Як відомо з курсів теоретичної механіки і опору матеріалів, задача про знаходження сил лег­ко розв'язується для статично визначених систем. Статично визначеною системоюназивають таку систему, в якій кількість невідомих сил дорів­нює числу рівнянь рівноваги, які можна скласти для їх знаходження.

Тому, перше ніж приступати до розв'язування задачі знаходження невідо­мих сил, треба з'ясувати, для яких кінематичних ланцюгів дотримується умова статичної визначеності. Для прикладу розглянемо плоский механізм, у склад якого входить п рухомих ланок, р₅ кінематичних пар п'ятого класу і р₄ кіне­матичних пар четвертого класу. Для того, щоб визначити реакції у кінематичних парах, необхідно щоб були відомі всі зовнішні сили (включаючи сили інерції), які діють на ланки механізму. Для кожної ланки плоского механізму можна скласти три рівняння, тому для п ланок - Зп рівнянь. Будь-яка сила характеризується трьома параметрами: величиною (модулем), напрямком і точкою прикладання. Розглянемо які з цих параметрів відомі, а які невідомі для сил реакцій у різних кінематичних парах плоских механізмів

Сили реакцій (сили взаємодії) між двома тілами (ланками), які стикають­ся, при відсутності тертя завжди напрямлені нормально до стичних поверхонь

Тому в обертовій кінематичній парі (рис. 4.3, а) реакція R₂₁, яка прикладена до ланки 2 зі сторони ланки 1, буде завжди проходити через центр шарніра О. Вели­чина і напрямок дії цієї сили R₂₁ невідомі, тому що вони залежать від сил, які прикладені до ланок 1 і 2.

Сказане повністю відноситься і до реакції R₁₂ , яка прикладена до ланки і зі сторони ланки 2, тому що сили взаємодії зв'язані між собою третім законом Ньютона: R₂₁=-R_12.

У поступальній парі (рис. 4.3, б) результуюча реакція R₂₁ буде направлена перпендикулярно до осі руху х - х ланок цієї пари, при цьому невідомими лишаються її величина і точка прикладання С .

У вищій парі IV класу (рис. 4.3, в) реакція R₂₁ направлена вздовж спільної нормалі п-п (без урахування сил тертя) і прикладена в точці до­тику С. Тому в такій кінематичній парі відомі точка прикладання і напря­мок сили реакції. Невідомою є її величина.

Тоді для плоского кінематичного ланцюга кількість невідомих дорівнюватиме 2р₅ + р₄.

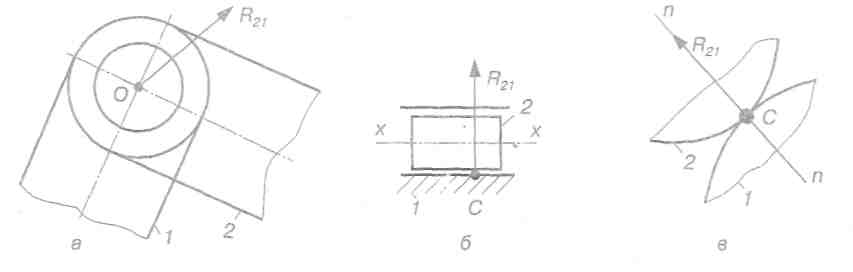
Рис. 4.3. Реакції в кінематичних парах:

а) обертовій парі V класу; б) поступальній парі V класу; в) парі IV класу

Кінематичний ланцюг буде статично визначений, коли число неві­домих параметрів дорівнює числу рівнянь, тобто в нашому випадку по­винна дотримуватись рівність

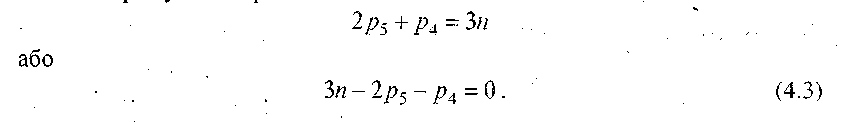
Вираз, який знаходиться в лівій частині рівності (4.3), показує число ступенів вільності плоского кінематичного ланцюга (2.7).

Отже, статично визначеними є кінематичні ланцюги з нульо­вим ступенем вільності. Такими кінематичними ланцюгами є структурні групи (2.10). Звідси випливає, що структурні групи є статично визначе­ними, а тому при силовому розрахунку доцільно розглядати рівновагу окремих структурних груп.

Умова (4.3) справедлива для плоскої системи зовнішніх сил, які діють на ланки механізму. При просторовому розташуванні сил число рів­нянь статики і число невідомих складових реакцій повинні відповідати умові (2.11). Статично визначений механізм не повинен мати зайвих зв'язків. Наявність таких зв'язків збільшує число невідомих складових ре­акцій; і для їх визначення додатково до рівнянь статики повинні бути складені рівняння деформацій.

Методика і порядок силового розрахунку механізмів. На під­ставі сказаного раніше можна викласти методику силового розрахунку ме­ханізмів. При силовому розрахунку механізм розбивають на структурні групи, тобто на статично визначені ланцюги, до яких прикладають усі зовнішні сили, включаючи сили (моменти сил) інерції, дію основного механізму на ланки групи замінюють реакціями. Під дією всіх цих сил група знаходиться у рівновазі, а тому можна скласти відповідну кількість рівнянь рівноваги, розв'язуючи які відносно невідомих складових реакцій, знаходимо їх. Причо­му, на відміну від кінематичного дослідження механізмів, силовий розрахунок починають з останньої від початкової ланки приєднаної структурної групи і закінчують силовим розрахунком початкової (початкових) ланки.

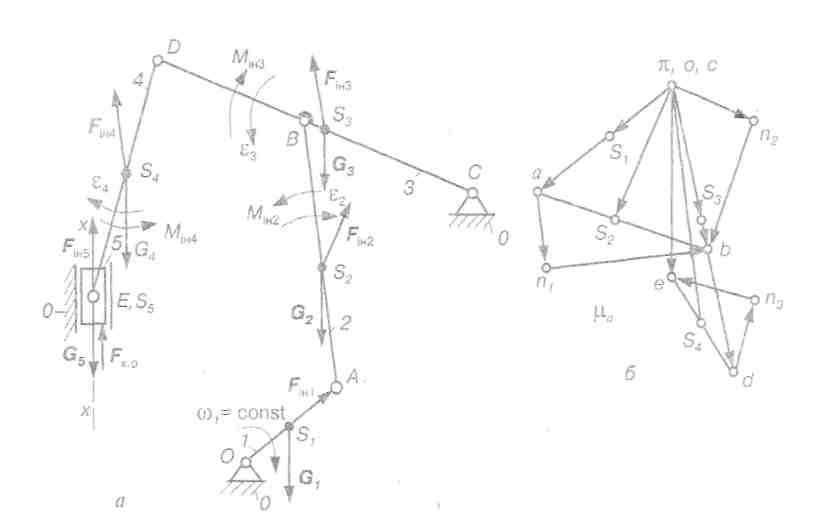
Таким чином, силовий розрахунок механізмів зводиться до розра­хунку окремих структурних груп. Послідовність силового розрахунку структурних груп II класу наведена в табл. 4.1 [15].

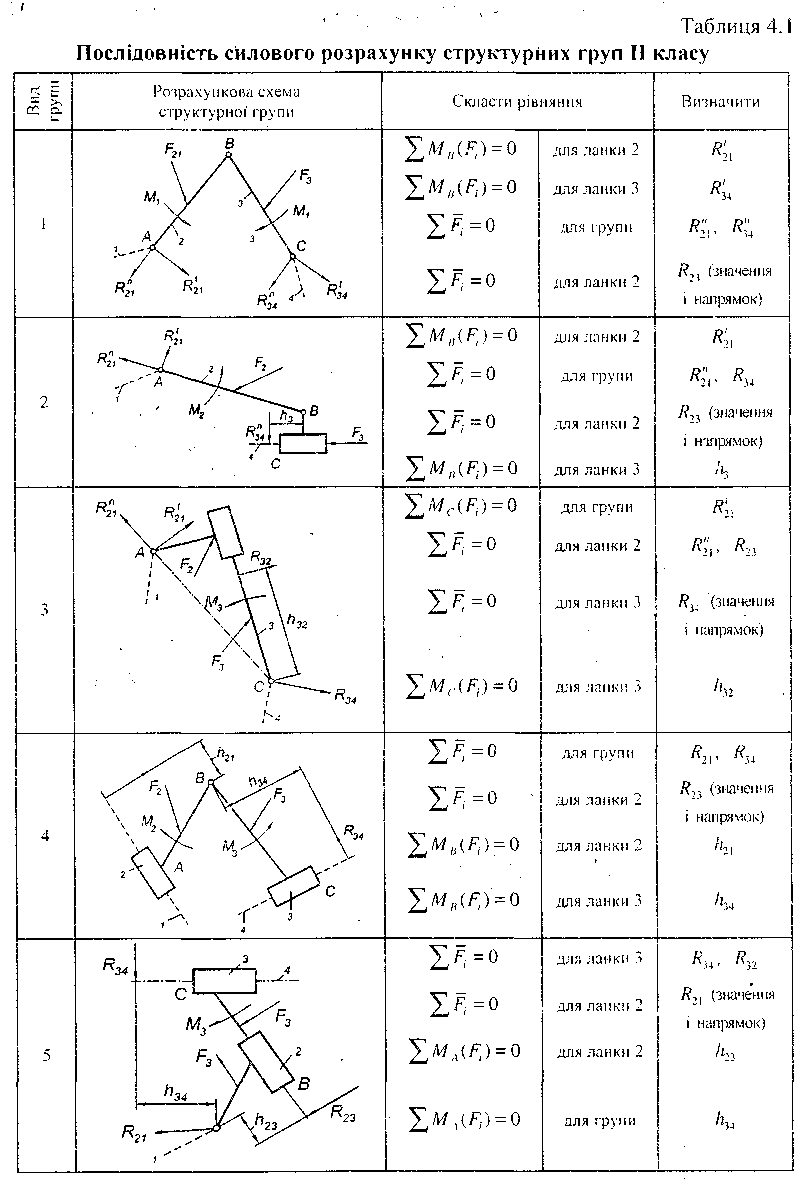
Методику та порядок силового розрахунку плоских механізмів розглянемо на прикладі шестиланкового механізму преса (рис. 4.4).

Приклад 4.1. Виконати силовий розрахунок шестиланкового механі­зму преса, кінематична схема якого показана на рис. 4.4, а. Задані швидкість обертання кривошипа w₁ , маси ланок – т₁, т₂, т₃, т₄, т₅ ; моменти інерції ланок відносно осей, які проходять через їх центри мас -

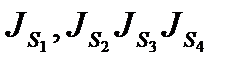;виробничий опір F_кo (сила корисного опору). Зрівноважувальну силу при­класти до кривошипа 1 у точці А перпендикулярно до лінії О А.

Розв'язання.Перше ніж розпочати силовий розрахунок механіз­му, необхідно визначити швидкості й прискорення всіх його ланок, а та­кож усіх точок, до яких прикладені сили (див. п. 3.5.3). На рис. 4.4, б для зручності знаходження сил інерції і їх моментів наведено план приско­рення цього механізму (див. п. 3.5.3, рис. 3.9).

Визначення сил інерції ланок. Величини сил інерції ланок і їх мо­менти визначаємо за формулами (4.1) і (4.2):

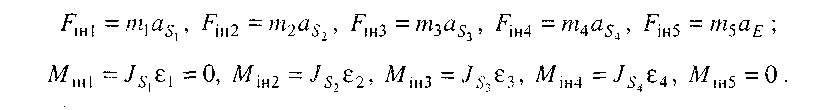
Вектори сил інерції прикладаємо в центрах мас відповідних ланок і на­правляємо їх у протилежний бік від прискорень центрів мас Моменти сил інер­ції направляємо в протилежний бік від кутових прискорень ланок (рис. 4.4, а).

На розрахунковій схемі (рис. 4.4, а), крім цього, показані вектори сил

тяжіння G_і , величини яких G_і = 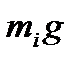, де g - прискорення вільного падіння.

Визначивши сили інерції ланок механізму, ми у даному разі розв'язали перше завдання силового розрахунку - знайшли всі зовнішні сили, які діють на ланки механізму, включаючи сили інерції. Після цього можна розпочати визначення реакцій у кінематичних парах і знаходження зрівноважувальної сили (моменту сили).

Рис. 4.4. До силового розрахунку механізмів:

а) розрахункова схема механізму; б) план прискорень

Визначення реакцій у кінематичних парах. Для цього розбиваємо механізм на групи Ассура. Механізм преса (рис, 4.4, а) складається з меха­нізму І класу (кривошип 1 і стояк 0) та двох груп ІI класу: група 2-3 - І ви­ду, група 4-5 - II виду. Силовий розрахунок починають з останньої приєд­наної групи, у нашому випадку з групи 4-5.

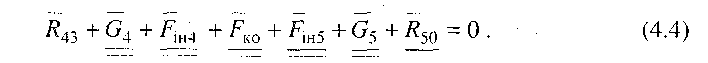
Для побудови плану сил необхідно, щоб кожний вектор сили був ві­домий як за величиною так і за напрямком. Домовимося надалі підкреслю­вати вектор сили рисками залежно від кількості відомих (відомими вва­жаються і величина, й напрямок сили).

У рівнянні (4.4) відомими є сили підкреслені двома рисками, неві­домі - реакції R₄₃ і R₅₀ (відомий напрямом), тобто три невідомі. Момент М_ін4 у це рівняння не входять, оскільки момент сил - це пара сил, які направлені в протилежні боки. Реакція в обертовій кінематичній парі Е до рі­вняння (4.4) також не входить, тому що вона для групи в цілому є внутрі­шня сила: з якою силою ланка 5 діє на ланку 4, з такою ж силою ланка 4 діє на ланку 5 (R₄₅ =-R₅₄ ).

Задача зі знаходження сил може розв'язуватися аналітично й гра­фічно. У першому випадку рівняння (4.4) записується у вигляді проекцій на координатні осі. При необхідності складають додаткові рівняння з та­ким розрахунком, щоб кількість усіх рівнянь дорівнювала числу невідомих (у нашому випадку - три).

На практиці, особливо в навчальному процесі та на стадії складання комп'ютерних програм, досить широко використовується графічний спосіб ви­значення сил шляхом побудови планів сил.Це пояснюється тим, що графічний метод не тільки наочний, добре розкриває методику силового розрахунку, але й дає достатню для практики точність досліджень, що дозволяє порівнянно легко контролювати достовірність аналітичного розрахунків.

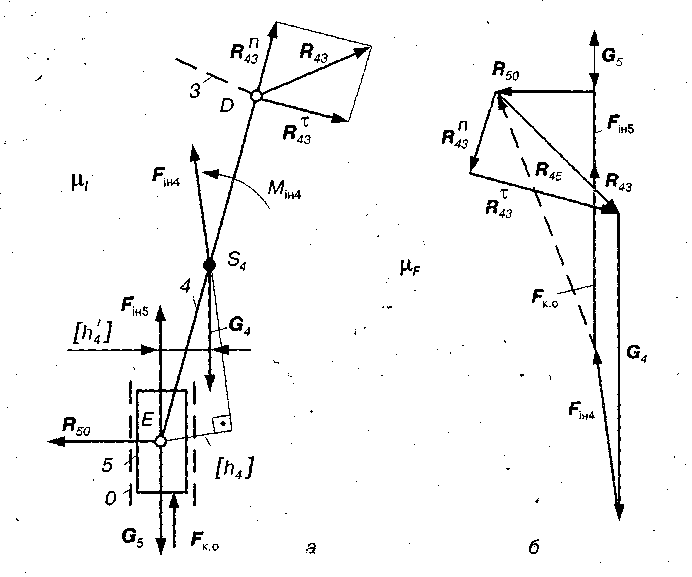
Рис. 4.5. Силовий розрахунок структурної групи 4-5:

а) розрахункова схема групи; б) план сил

Для побудови плану сил у рівнянні рівноваги (4.4) може бути не більше двох невідомих. У нашому випадку необхідно зменшити кількість невідомих з 3 до 2. У цьому рівнянні маємо три невідомі (величина і на­прямок реакції R₄₃ і величина реакції R₅₀ ). Розкладаємо вектор R₄₃ на дві складові: нормальну R 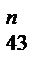й дотичну R 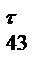, тобто

Складаємо рівняння рівноваги моментів усіх сил, що діють на ланку 4, відносно точки Е (рис. 4.5, а):

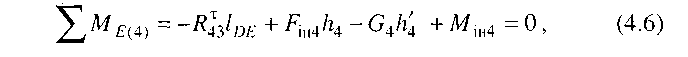
звідки

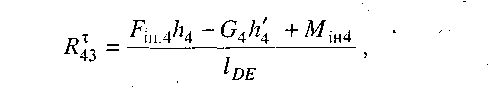
У рівнянні (4.6) і далі цифра 4, яка вказана в дужках, показує но­мер ланки, рівновага якої розглядається.

Підставивши (4.5) у рівняння (4.4), маємо

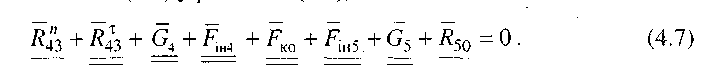
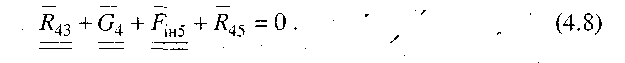
У цьому рівнянні невідома тільки реакція R₄₅ (за величиною і на­прямком). Для її знаходження будуємо план сил, використовуючи (4.8). У нашому випадку досить з'єднати початок вектора R₄₃ з кінцем вектора F_ін (на рис. 4.5, б вектор R₄₅ показаний штриховою лінією). Треба відмі­тити, що така побудова можлива тільки тоді, коли сили, які діють на кожну ланку, згруповані в рівнянні (4.7) так, що сили, які діють на ланку 4 - ліво­руч, на ланку 5 - праворуч.

Точку прикладання реакції R₅₀ (рис. 4,5, а) знаходимо з рівняння моментів усіх сил, що діють на ланку 5, відносно точки Е, але, враховую­чи, що всі сили, які діють на ланку 5, перетинаються у точці Е, то й реак­ція R₅₀ також проходитиме через точку Е.

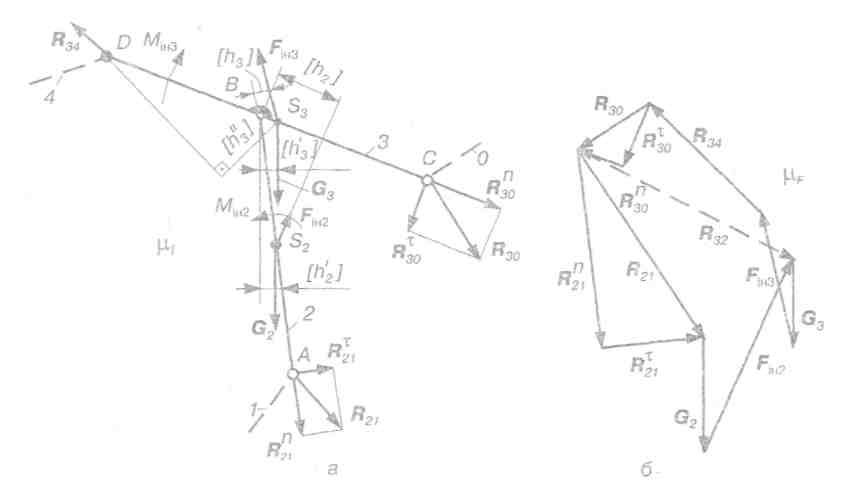
Рис. 4.6. Силовий розрахунок структурної групи 2-3:

а) розрахункова схема групи; б) план сил

дотичні - перпендикулярно до них). Величину дотичних складових знаходимо з рівнянь моментів сил, які діють відповідно на ланки2 і 3, відносно точки В:

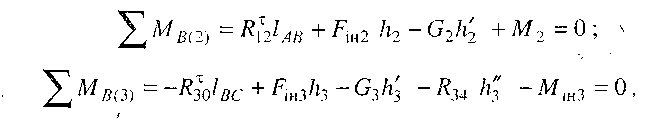
звідки

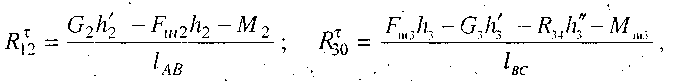
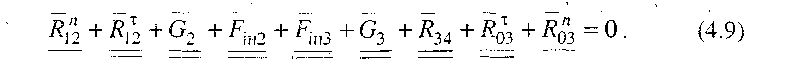
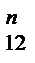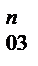Згідно з рівнянням (4.9) будуємо план сил (рис. 4.6,6), послідовно відкладаючи у вибраному масштабі всі вектори, точка перетину напрямків R і R визначить їхню величину і дійсний напрямок. Тоді

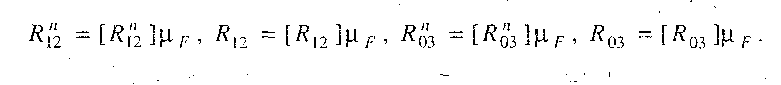
Реакцію в обертовій парі В знаходимо з рівноваги ланки 2:

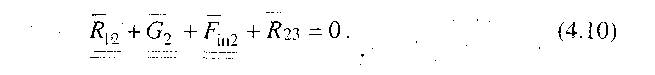
У цьому рівнянні невідома тільки реакція R₂₃, яку можна знайти, побудувавши план сил за рівнянням (4.9). На рис. 4.6, б реакція R₂₃=-R₃₂,показана штриховою лінією.

Силовий розрахунок механізму закінчується силовим розрахунком механізму І класу (кривошипа 1).

Силовий розрахунок механізму І класу. До кривошипа 1 (рис. 4.7, а) прикладаємо всі зовнішні сили, включаючи сили інерції які діють на нього (G_1,F_ін1 ). Крім цього, на кривошип 1 у точці А діє реакція R₁₂ зі сторони ланки 2 групи Ассура, приєднаної до нього. Ця реакція дорівнює за величиною реакції R₂₁, але направлена в протилежний бік Реакція R₂₁ вже визначена при силовому розрахунку приєднаної структурної групи, тобто R₁₂ = -R_21. Крім цього, у кінематичній парі О на кривошип діє сила реакції R₁₀ з боку стояка. Цю

реакцію треба визначити. Проте, як випливає з формули (4.3), кривошип 1 під дією прикладених до нього сил, у тому числі й сил інерції, не перебуває у рівнова­зі, тому що при одній рухомій ланці й одній парі V класу число рівнянь рівноваги яке можна скласти, буде на одиницю більше числа невідомих, що треба визначи­ти, тобто

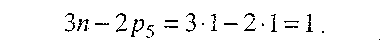
Для того, щоб була забезпечена рівновага кривошипа, необхідно додатково ввести силу або пару сил, які зрівноважують усі сили, прикла­дені до нього. Цю силу називають зрівноважувальною силою, а момент пари сил - зрівноважувальним моментом. Умовимось зрівноважувальну силу позначати через F_зр , а зрівноважувальний момент - М_зр . Точка при­кладання і напрямок зрівноважувальної сили (моменту) мають бути задані або визначені з конструкції приводу початкової ланки. Наприклад, якщо вал кривошипа 1 зв'язаний з двигуном за допомогою муфти, то треба при­класти до кривошипа 1 зрівноважувальний момент М_зр, якщо цей вал з'єднаний з двигуном за допомогою зубчастої передачі, то до кривошипа треба прикласти зрівноважувальну силу, яка діятиме вздовж нормалі до профілю зубців (вздовж лінії зачеплення, див. розд. 9). Залежно від того, що діє - сила F_зр (і як вона прикладена) чи момент М_зр, - реакція R₁₀ у кінематичній парі О буде різна.

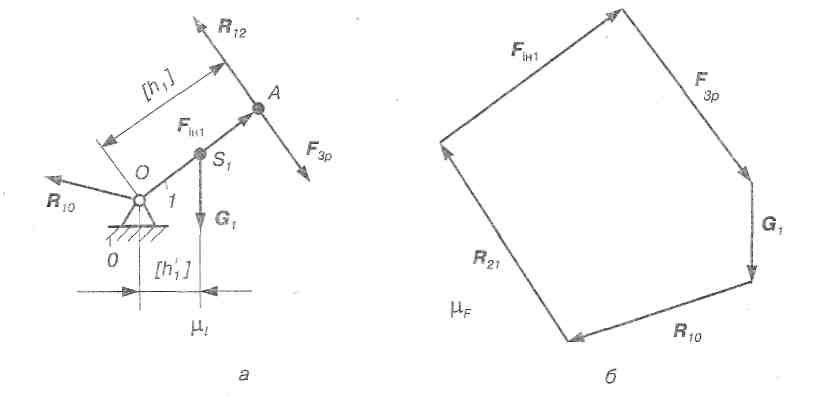
Рис. 4.7. Силовий розрахунок механізму І класу:

а) розрахункова схема групи; б) план сил

Зрівноважувальна сила або зрівноважувальний момент є та­кою силою або моментом, які необхідно прикласти до початкової лан­ки, щоб вона рухалася за заданим законом (як правило рух початкової ланки приймають рівномірним). У робочих машинах зрівноважувальну силу (момент) можна собі уявити, як деяку ідеальну (умовну) рушійну си­лу, яку треба прикласти до початкової ланки, щоб дотриматися заданого закону руху; у машинах-двигунах, навпаки, як деяку ідеальну силу опору. Проте реальні сили, які прикладені до початкової ланки, як правило, від­різняються від зрівноважувальної сили (моменту), а тому дійсний рух по­чаткової ланки відрізнятиметься від заданого, тобто w₁ =const .Про це йтиметься в розділі 5.

Нехай зрівноважу вальна сила F_зр буде прикладена у точці А, як це показано на рис. 4.7, а. Її величину можна знайти з рівноваги кривошипа 1 відносно точки О, записавши рівняння моментів усіх сил, що діють на нього:

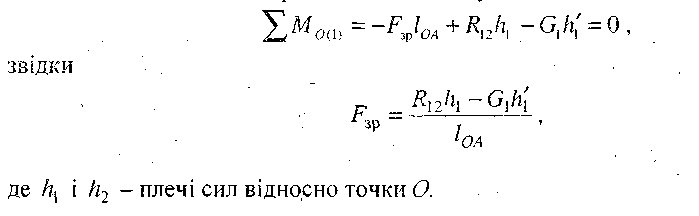
Для знаходження реакції R₁₀ складаємо рівняння рівноваги кри­вошипа 1:

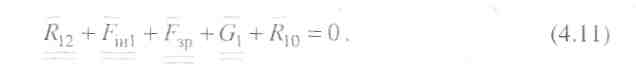
У цьому рівнянні невідома тільки реакція R₁₀, яку знаходимо по­будовою плану сил (рис. 4.7, б). Якщо величина зрівноважувальної сили, одержана з рівнянь (4.11), буде від'ємною, треба на плані сил змінити її напрямок на протилежний.

Якщо до початкової ланки прикласти зрівноважувальний момент, методика силового розрахунку не змінюється, змінюється лише величина і напрямок реакції R₁₀ .