Важіль М. Є. Жуковського
У тому разі, коли нема потреби робити повний силовий розрахунок механізму, в результаті якого визначаються реакції в кінематичних парах (наприклад, розрахунок потужності двигуна), задача зводиться тільки до визначення зрівноважувальної сили або зрівноважувального моменту, який прикладають до початкової ланки. Реакції в кінематичних парах можуть залишатися невідомими, як внутрішні сили для всього механізму в цілому. У таких випадках для знаходження зрівноважувальної сили користуються методом (правилом) так званого ,,жорсткого" важеля М. Є. Жуковського. Правило М.Є. Жуковського ґрунтується на використанні принципу можливих переміщень, згідно з яким, якщо на будь-яку механічну систему діє ряд сил, то, приєднавши до заданих сил сили інерції і надавиш всій системі можливих для даного її положення переміщень, дістанемо ряд елементарних робіт, сума яких дорівнює нулю.
Для механізму, в якому ланки здійснюють визначений рух, можливі переміщення стають дійсними переміщення. Тоді, якщо на ланки механізму діє ряд сил F1,, F2 , F3……,Fn ,принцип можливих переміщень можна виразити в такому вигляді:
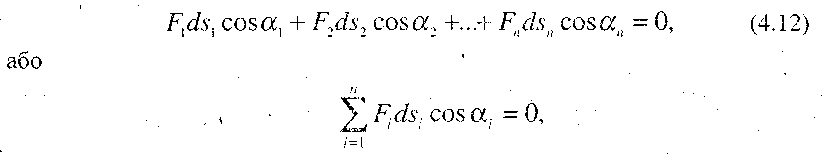

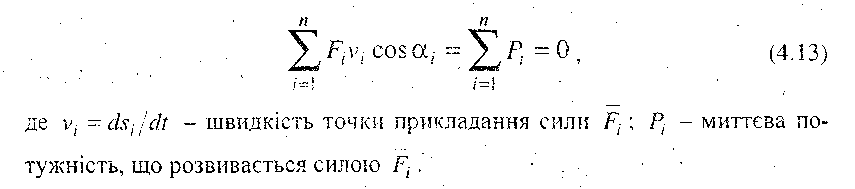
Рівняння (4.13)-показує, що принцип можливих переміщень можна виразити через суму миттєвих потужностей сил, що діють на ланки механізму. Для окремо взятої ланки АВ (рис. 4.8, а), на яку діє сила Fі, що прикладена в точці С (швидкість точок А і В задані, точка Р - миттєвий центр швидкостей), миттєва потужність, що розвиває ця сила,
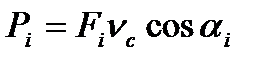
може бути виражена по-іншому. Для нього будуємо повернутий на 90° проти миттєвого обертання ланки АВ план швидкостей цієї ланки (рис. 4.8, б), у точку с якого прикладаємо силу Fi, і запишемо момент сили Fі відносно полюса р:
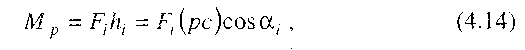
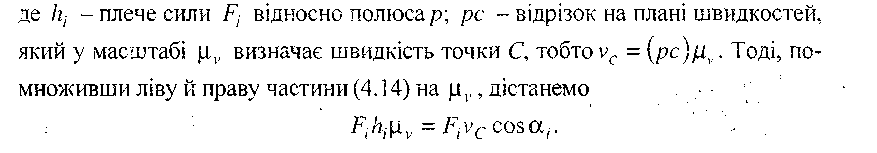


Рівняння (4.15) і є записане в математичній формі правило важеля М. Є. Жуковського,яке можна сформулювати так.
Переносимо всі задані сили, що діють у даний момент часу на ланки механізму, у тому числі й сили інерції, в однойменні точки повернутого плану швидкостей, не змінюючи при цьому величини і напрямку сили. Розглядаємо повернутий план швидкостей як деякий жорсткий важіль, який знаходиться в рівновазі відносно полюса плану швидкостей під дією всіх прикладених сил. Тоді сума моментів усіх цих сил, включаючи зрівноважувальну силу, відносно полюса плану швидкостей дорівнює нулю.
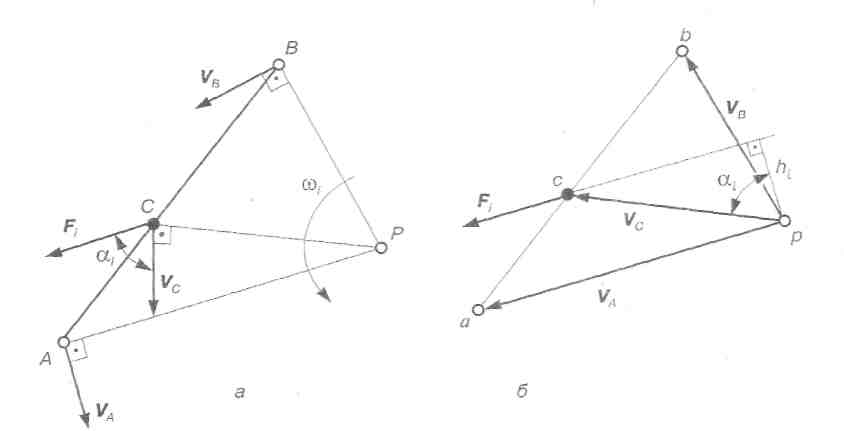
Рис. 4.8. До виводу правила важеля М. Є. Жуковського
Така геометрична інтерпретація принципу можливих переміщень дуже зручна для розв'язування задач динаміки механізмів. Метод цей дістав назву методу М.Є.Жуковського за ім'ям великого російського механіка, який його запропонував, а важіль, яким користуються в цьому методі, названо важелем Жуковського.
Метод Жуковського можна застосувати для знаходження величини будь-якої сили, якщо точку прикладання і напрямок цієї сили задано, а також задано значення, напрямки і точка прикладання всіх інших сил. Справді, у цьому випадку в рівнянні (4.15) буде тільки одне невідоме значення шуканої сили, яка з нього визначається.
Якщо на ланки механізму, крім сил Fi, діють ще пара сил, моментом, яких є Мi, то при використанні правила Жуковського кожний момент Мi, (рис. 4.9) розкладають на пару сил F 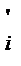 які прикладають у дві точки, наприклад А і В.
які прикладають у дві точки, наприклад А і В.
Величину й напрямок кожної сили Fi' визначають за умови, що Мі – Fi'Іi, де Fi' = Мі / lі, li; - плече сил Fi', що дорівнює в нашому випадку (рис. 4.9) довжині ланки АB (li= lАB). При цьому напрямок моменту пари сил Fi' повинен збігаються з напрямком моменту Мi, Треба мати на увазі, що напрямок цього моменту сил F  на важелі Жуковського може не збігатися з напрямком моменту Мi, на схемі механізму. Це буває тоді, коли положення букв А і В на ланці та на плані швидкостей (а і b ) не збігаються.
на важелі Жуковського може не збігатися з напрямком моменту Мi, на схемі механізму. Це буває тоді, коли положення букв А і В на ланці та на плані швидкостей (а і b ) не збігаються.
Розглянемо приклад визначення зрівноважувальної сили Fзр за допомогою правила важеля Жуковського.
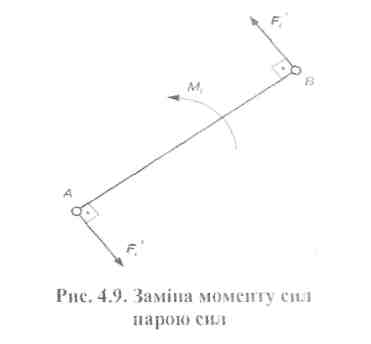
Рис. 4.9. Заміна моменту сил парою сил
Приклад 4.2 Нехай буде задана кінематична схема кривошипно-повзунного механізму (рис. 4.10, а), на ланки якого діють сили F1,F2,F3,момент сил М2 швидкість обертання кривошипа ОА w1. Зрівноважувальну силу прикласти до кривошипа ОА у точці А і направити перпендикулярно до лінії О А.
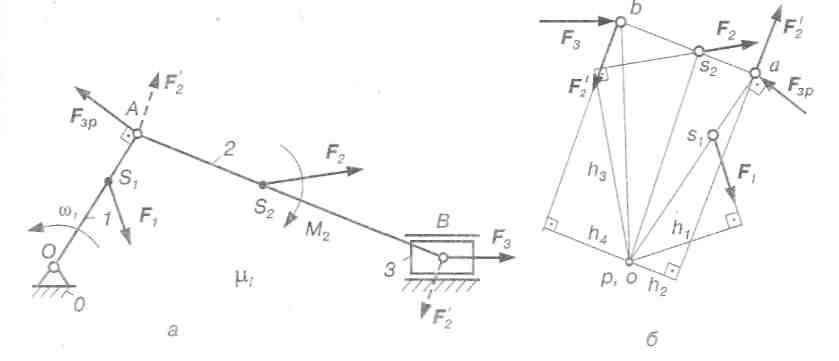
Рис. 4.10. Визначення зрівноважувальної сили за допомогою правила важеля Жуковського:
а) розрахункова схема; б) важіль Жуковського
Розв'язання. Будуємо для заданого положення механізму повернутий на 90 проти миттєвого обертання кривошипа w1, план швидкостей (рис. 4.10, б), в відповідних точках якого прикладаємо сили F1,F2,F3,Fзр;момент М2 розкладаємо на пару сил F2 = М2/lАВ (на рис. 4.І0, а сили F2 показані штриховою лінією), які прикладаємо відповідно у точках а і b перпендикулярно до АВ (аb II АВ).
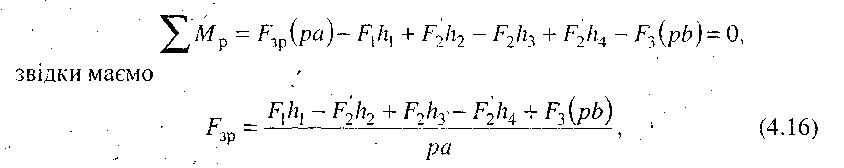
|
Враховуючи, що під дією цих сил, включаючи зрівноважувальну силу, механізм знаходиться у рівновазі, можна записати таке рівняння моментів сил, що прикладені до повернутого плану швидкостей, який умовно приймаємо жорстким важелем:
де hi - плечі відповідних сил відносно полюса повернутого плану швидкостей, мм.
Напрямок вектора зрівноважувальної сили Fзр вибрано правильно, якщо після числового розрахунку (4.16) одержимо Fзр із знаком плюс і, навпаки, якщо знак буде мінус, то треба змінити напрямок вектора сили Fзр на протилежний. Викладений метод є загальним для механізмів будь-якого класу.
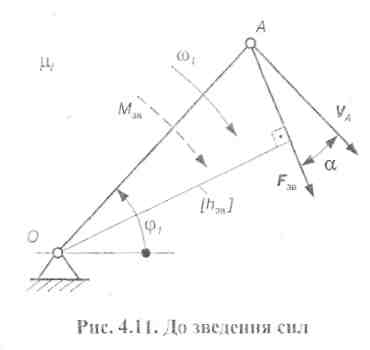
При динамічному дослідженні руху механізмів зручно всі сили, що діють на різні ланки механізму, замінити однією силою або моментом сил, які прикладають до однієї з ланок механізму. Таку силу, що замінює всі інші сили, називають зведеною силою, а момент сили - зведеним моментом. Для того щоб така заміна була еквівалентною, необхідно, щоб робота зведеної сили (моменту сили) на деякому можливому переміщенні її точок прикладання або потужність, яку вона розвиває, має відповідно дорівнювати сумі робіт, прикладених до механізму сил на тому самому переміщенні їх точок прикладання, або сумі потужностей, що розвиваються цими силами. Це і є умовою зведення сил або моментів сил.
Ланку механізму, до якої прикладають зведену силу, називають лапкою зведення, а точку їх прикладання - точкою зведення. Якщо механізм має один ступінь вільності, то для вивчення його руху досить знати закон руху однієї з його ланок, тобто знати закон зміни узагальненої координати
Як правило, ланкою зведення обирають початкову ланку механізму. У робочих машинах ланкою зведення обирають головний вал, у машинах-двигунах - вихідний вал. Тоді замість того, щоб розглянути всі ланки механізму чи машини, можна розглянути тільки одну ланку, наприклад кривошип О А (рис. 4.11), узагальнена координата якого - кут 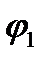 ,.
,.
Для визначення зведених сил зручно використовувати рівність потужностей

У цій рівності Рзв - потужність, яку розвиває зведена сила Fзв або зведений момент Мзв; Рi - потужність, що розвивають сили та моменти пар сил, які прикладені до i-ої ланки та мають бути зведені (і = 1,2,3,..., п). Ці потужності можна записати в такому вигляді:
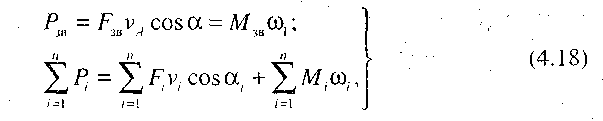

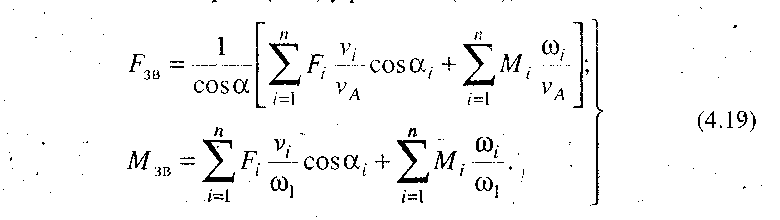
З рівнянь (4.19) видно, що при заданих силах Fі і моментах Мі визначення зведеної сили Fзв або зведеного моменту Мзв не становить значних труднощів і може бути зроблене, якщо для всіх положень, які досліджуються, визначені швидкості ланок механізму.
Для визначення Fзв і Мзв за формулами (4.19) необов'язково знати
справжні швидкості точок і ланок, тому що вони входять у вигляді відношення двох швидкостей, які не залежить від величини швидкості руху механізму, а тільки від положень його ланок і можуть бути подані через відповідні відрізки плану швидкостей. Цей план можна будувати для довільно вибраної кутової швидкості ланки зведення, тобто в невизначеному масштабі.
Цілком очевидно, що між зведеною силою і зведеним моментом сил існує такий зв'язок:

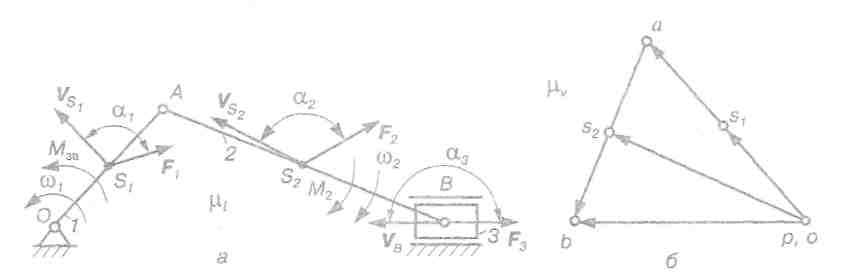
Ряс. 4.12. До визначення зведеної сили: а) розрахункова схема; б) план швидкостей
Приклад 4.3. На ланки кривошипно-повзунного механізму (рис. 4.12, а) діють сили F1F2,F3 і момент сил М2.Визначити зведений момент сил, який прикласти до кривошипа 1. План швидкостей механізму наведено на рис. 4.12, б.
Розв'язання. Для розв'язання цієї задачі використовуємо рівність потужностей (4.17). У нашому випадку
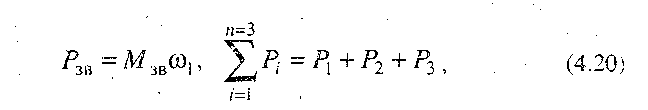
де Р1,Р2,Р3 - потужності, які розвивають сили, що прикладені відповідно до ланок 1, 2, 3:
P1 = 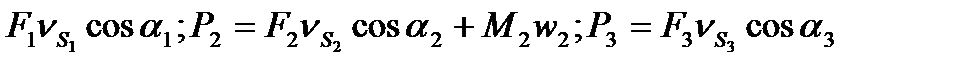 (4.21)
(4.21)
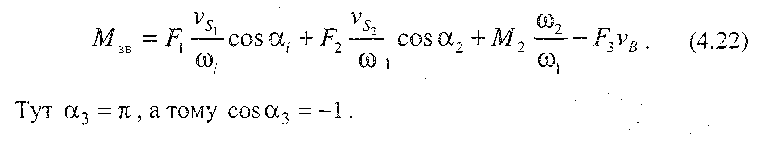
Дата добавления: 2016-06-15; просмотров: 5178;











