Деление прямых кодов чисел

Рассмотрим два базовых метода выполнения операции деления: деление с восстановлением остатка и деление без восстановления остатка.

При делении с восстановлением остатка каждый цикл распадается на три такта. В первом такте очередной частичный остаток и регистр частного сдвигаются на один разряд влево. Во втором такте из сдвинутого частичного остатка вычитается делитель. В третьем такте в младший разряд регистра частного заносится очередная цифра, определяемая инверсией знакового разряда сумматора, и в случае отрицательного сумматора выполняется восстановление остатка путем прибавления к содержимому сумматора положительного делителя. Выполнение проверки на возможность деления можно рассматривать как нулевой цикл с пропущенным первым тактом, т.е. в случае отрицательного сумматора в младший разряд регистра частного заносится нуль, а делимое подлежит восстановлению.

Пример.

[А]_пр = 0,110001, [Р_А]_пр = 1,011;

[В]_пр = 1,100101, [Р_В]_пр = 0,001;

С = А/В.

1. Определение знака частного.

Зн_С = Зн_А Å Зн_В = 0 Å 1 = 1.

.

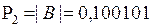2. Определение порядка частного.

Р_С = Р_А – Р_В.

+

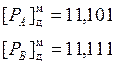
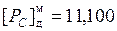
В прямом коде порядок частного может быть записан как .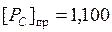

3. Деление мантисс.

Частное Делитель

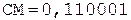
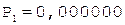
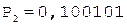
0.

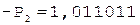
> 0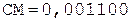, переполнение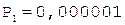

1.

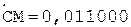
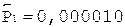
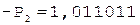
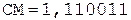
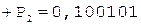
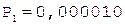
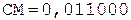
2.

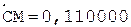
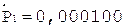
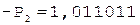
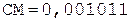
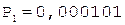
3.

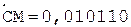
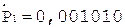
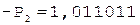
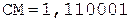
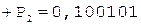
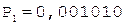
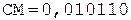
4.

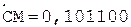
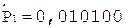
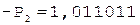
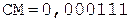
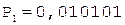
5.

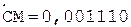
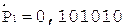
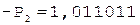
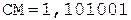
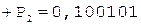
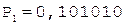
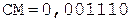
6.

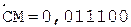
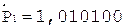
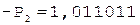
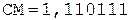
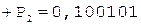
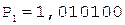
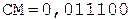
Таким образом, в результате выполнения шести основных циклов деления получены семь цифр частного. Единица в знаковом разряде регистра частного указывает на денормализацию влево. После нормализации и последующего присвоения знака результат может быть записан как

[С]_пр = 1,101010, [Р_С]_пр = 1,011.

В ЭВМ деление чисел с восстановлением остатка практически не применяется, поскольку восстановление остатка требует дополнительных временных затрат, а если оно не требуется, то цикл деления получается неравномерным.

Рассмотрим еще один метод деления чисел, при котором в случае появления отрицательного частичного остатка восстановление не производится, а происходит переход к следующему циклу деления, в котором отрицательный частичный остаток удваивается и к нему прибавляется положительный делитель. При этом цифры частного формируются так же, как и в предыдущем методе, т.е. путем инвертирования знакового разряда. При выполнении проверки на деление в нулевом цикле отрицательный сумматор можно не восстанавливать.

Таким образом, каждый из n циклов деления состоит из двух тактов. В первом такте очередной частичный остаток и регистр частного сдвигаются на один разряд влево. Во втором такте выполняется арифметическая операция, определяемая знаком сумматора или цифрой частного, определенной в предыдущем цикле. Если сумматор больше нуля (предыдущая цифра частного – единица), то из удвоенного (сдвинутого влево) очередного частичного остатка вычитается делитель. В противном случае к удвоенному очередному частичному остатку следует прибавить положительный делитель.

При использовании немодифицированного кода анализ знака сумматора необходимо делать до начала очередного цикла деления, так как в некоторых случаях при удвоении остатка его знак может быть потерян.
В этом случае алгоритм распадается на две части (две ветви) со сдвигом в каждой, т.е. анализ знака сумматора выполняется до сдвига.

При использовании модифицированного кода необходимость в разделении алгоритма на две ветви или в анализе предыдущей цифры частного отпадает, так как тип арифметической операции может быть определен по старшему знаковому разряду сумматора.

Пример.

[А]_пр = 0,110001, [Р_А]_пр = 0,100;

[В]_пр = 1,100101, [Р_В]_пр = 0,011;

С = А/В.

1. Определение знака частного.

Зн_С = Зн_А Å Зн_В = 0 Å 1 = 1.

.

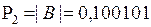2. Определение порядка частного.

+

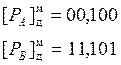
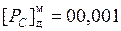
3. Деление мантисс.

Частное Делитель

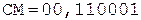
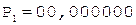
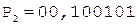
0.

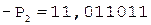
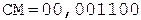> 0, переполнение

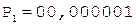
1.

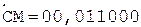
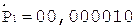
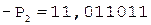
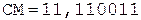
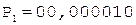
2.

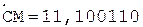
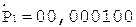
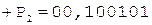
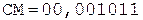
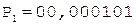
3.

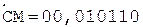
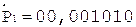
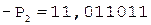
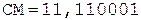
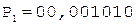
4.

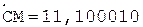
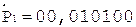
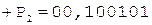
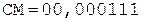
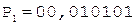
5.

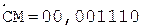
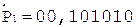
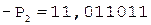
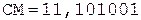
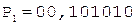
6.

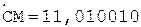
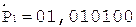
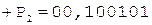
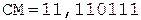
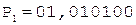
После устранения денормализации и присвоения знака результат может быть записан в следующем виде:

[С]_пр = 1,101010, [Р_С]_пр = 0,010.