Ускоренное выполнение операции умножения
Рассмотрим два логических метода ускорения выполнения операции умножения младшими разрядами вперед: метод умножения с анализом последовательностей «0» и «1» в множителе (метод «преобразования» множителя, ускоренное умножение № 1) и метод расшифровки двух разрядов множителя (ускоренное умножение № 2). Первый метод позволяет уменьшить число арифметических операций на сумматоре, необходимых для формирования произведения (при этом число циклов умножения не сокращается). Второй метод позволяет сократить число циклов умножения вдвое, поскольку в каждом цикле множимое умножается сразу на два разряда множителя.
Метод «преобразования» множителя заключается в том, что в некоторых случаях число содержащихся в множителе единиц можно уменьшить, заменив их нулями, что приводит к пропуску такта суммирования, поскольку при умножении на 0 содержимое сумматора не изменяется. Следует понимать, что рассматриваемое преобразование множителя выполняется логически, т.е. реальное содержимое регистра множителя остается неизменным, но меняется процедура его обработки. Поэтому слово «преобразование» в названии метода взято в кавычки.
Пусть в множителе три или более идущих друг за другом разрядов 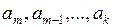 равны единице. В соответствии с элементарной двоичной арифметикой такая последовательность может быть представлена как разность двух чисел:
равны единице. В соответствии с элементарной двоичной арифметикой такая последовательность может быть представлена как разность двух чисел: 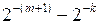 . Покажем это на примере множителя
. Покажем это на примере множителя
B = 0,011100:
|
|
 0,000100
0,000100
0,011100
Таким образом, арифметическую операцию сложения при умножении на множитель подобного вида можно заменить операцией вычитания множимого из суммы частичных произведений. После окончания последовательности подряд следующих единиц необходимо снова выполнять операцию сложения.
Отдельно стоящие нули или единицы могут увеличить число единиц в преобразованном множителе. Рассмотрим, например, фрагмент множителя, состоящий из нулей и единицы в i-м разряде, и его преобразованный вид:
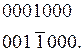
В этом случае умножение множимого A на преобразованный множитель должно выполняться в соответствии с выражением
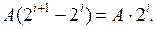
Если фрагмент множителя с нулем в i-м разряде и его преобразование имеют вид
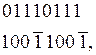
то умножение множимого A на преобразованный множитель должно выполняться в соответствии с выражением
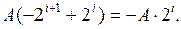
Для определения отдельно стоящих нулей и единиц будем анализировать одновременно два разряда множителя, а для выявления последовательностей идущих подряд нулей или единиц в множителе введем в устройство специальный запоминающий элемент, называемый триггером, имеющий два устойчивых состояния – «0» и «1». Тогда арифметические операции на сумматоре и установки триггера сдвига определятся в соответствии с табл. 2.2.
Таблица 2.2
| Разряды множителя | Состояние триггера Тг | Действия | |
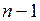
| n | ||
| – | |||
| СМ + А | |||
| – | |||
| СМ – А, Тг = 1 | |||
| СМ + А, Тг = 0 | |||
| – | |||
| СМ – А | |||
| – |
Следует отметить, что перед началом выполнения умножения триггер должен быть установлен в состояние «0». По окончании умножения триггер также должен установиться в «0», поэтому в некоторых случаях требуется выполнение дополнительного цикла умножения (точнее – полуцикла, поскольку такт сдвига не выполняется) для обработки последней единицы в множителе, который может быть совмещен с округлением результата.
При умножении мантисс следует использовать модифицированный код, поскольку в некоторых случаях может возникать переполнение разрядной сетки.
Определение знака и порядка произведения, его нормализация выполняются так же, как при неускоренном умножении.
Пример.
Умножим числа с фиксированной запятой.
[А]пр = 0,11001001;
[В]пр = 0,11101011;
С = А ´ В.
1. Определение знака произведения.
ЗнС = ЗнА Å ЗнВ = 0 Å 0.
2. Умножение мантисс.
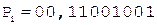 ;
;


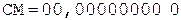
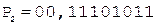
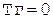
 1. -
1. - 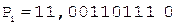
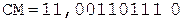
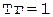

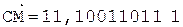
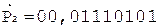
 2.
2. 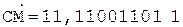
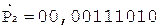
 3. -
3. - 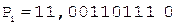
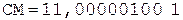

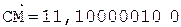
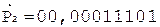
 4.
4. 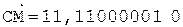
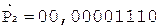
5. - 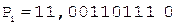
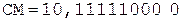

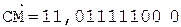
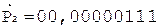
 6.
6. 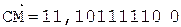
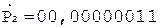
 7.
7. 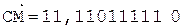
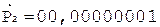
 8.
8. 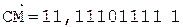
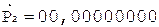
 9. +
9. + 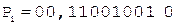
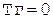
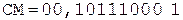 При совмещении операции округления с
При совмещении операции округления с
 Окр. +
Окр. + 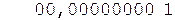 дополнительным 9-м циклом регистр мно-
дополнительным 9-м циклом регистр мно-
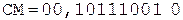 жимого имеет вид
жимого имеет вид 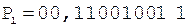 .
.
3. Ограничение результата восемью разрядами и присвоение знака.
Окончательно [С]пр = 0,10111001.
Рассмотрим второй ускоренный метод умножения, заключающийся в умножении на два разряда множителя одновременно. При этом возможны четыре двоичные комбинации младших разрядов:
1. Комбинация «00» означает умножение на 0, т.е. пропуск такта суммирования.
2. Комбинация «01» означает умножение на 1, т.е. прибавление множимого к предыдущему частичному произведению.
3. Комбинация «10» означает умножение на 2, т.е. прибавление к предыдущему частичному произведению удвоенного множимого (сдвинутого на один разряд влево).
4. Комбинация «11» означает умножение на 3. В этом случае вместо утроения множимого комбинацию «11» заменяют комбинацией « 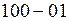 », т.е. «четыре минус один». Это означает, что из текущего частичного произведения следует вычесть множимое и сформировать единицу переноса в следующую пару разрядов множителя.
», т.е. «четыре минус один». Это означает, что из текущего частичного произведения следует вычесть множимое и сформировать единицу переноса в следующую пару разрядов множителя.
Таким образом, умножение выполняется за 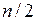 циклов, при этом каждый цикл распадается на два такта. В первом такте выполняется арифметическая операция, определяемая комбинацией двух младших разрядов множителя и переносом из предыдущей пары разрядов (табл. 2.3). Во втором такте содержимое сумматора и регистр множителя сдвигаются на два разряда вправо. Для запоминания переноса в следующую пару разрядов множителя можно использовать дополнительный триггер (Тг). При формировании переноса из двух старших разрядов множителя необходимо выполнить дополнительный такт сложения содержимого сумматора и множимого (полуцикл умножения).
циклов, при этом каждый цикл распадается на два такта. В первом такте выполняется арифметическая операция, определяемая комбинацией двух младших разрядов множителя и переносом из предыдущей пары разрядов (табл. 2.3). Во втором такте содержимое сумматора и регистр множителя сдвигаются на два разряда вправо. Для запоминания переноса в следующую пару разрядов множителя можно использовать дополнительный триггер (Тг). При формировании переноса из двух старших разрядов множителя необходимо выполнить дополнительный такт сложения содержимого сумматора и множимого (полуцикл умножения).
Таблица 2.3
| Разряды множителя | Перенос из предыдущей пары | Перенос в следующую пару | Действие | |
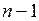
| 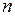
| |||
| – | ||||
| +А | ||||
| +2А | ||||
| –А | ||||
| +А | ||||
| +2А | ||||
| –А | ||||
| – |
Поскольку в некоторых случаях возможно переполнение разрядной сетки с искажением второго знакового разряда, следует использовать код с тремя знаковыми разрядами.
Определение знака и порядка произведения, его нормализация выполняются так же, как при неускоренном умножении.
Пример.
Умножим числа с фиксированной запятой.
[А]пр = 0,11101011;
[В]пр = 0,11001001;
С = А ´ В.
1. Определение знака произведения.
ЗнС = ЗнА Å ЗнВ = 0 Å 0.
2. Умножение мантисс.
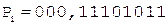 ;
;


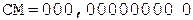
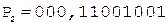
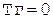
 1. +
1. + 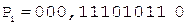
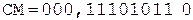

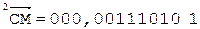
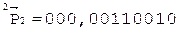
2. + 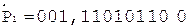

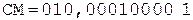

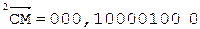
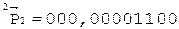
 3.
3. 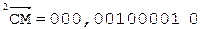
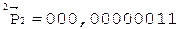
 4. -
4. - 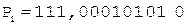
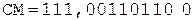
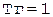
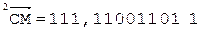
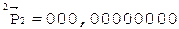
 5. +
5. + 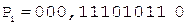
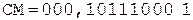
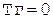 ;
;
 Окр. +
Окр. + 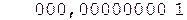 Округление результата может быть
Округление результата может быть
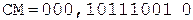 совмещено с 5-м циклом в один такт.
совмещено с 5-м циклом в один такт.
3. Ограничение результата восемью разрядами и присвоение знака.
Окончательно [С]пр = 0,10111001.
Ясно, что умножение рассмотренным методом может выполняться только начиная с младших разрядов множителя.
Дата добавления: 2020-02-05; просмотров: 1166;











