Ускоренное выполнение операции деления
В быстродействующих цифровых вычислительных устройствах применение вышеописанных алгоритмов деления нецелесообразно, поскольку для формирования n-разрядного частного необходимо выполнить не менее n арифметических операций (сложения или вычитания). Рассмотрим два логических метода ускорения выполнения операции деления, позволяющих сократить число выполняемых арифметических операций. Сразу оговоримся, что число циклов деления при использовании этих методов не уменьшается. Обязательным условием правильного выполнения приведенных алгоритмов является нормализованный делитель.
Первый ускоренный метод деления с анализом одного разряда основан на следующих соображениях. Будем полагать, что очередной частичный остаток 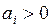 , а нормализованный делитель
, а нормализованный делитель 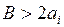 , т.е. делитель больше остатка, сдвинутого влево на один разряд. Очевидно, что в следующем цикле деления из удвоенного частичного остатка следует вычесть делитель. В результате на сумматоре сформируется число
, т.е. делитель больше остатка, сдвинутого влево на один разряд. Очевидно, что в следующем цикле деления из удвоенного частичного остатка следует вычесть делитель. В результате на сумматоре сформируется число 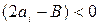 , что приводит к формированию очередной цифры частного, равной нулю.
, что приводит к формированию очередной цифры частного, равной нулю.
В следующем цикле деления очередной отрицательный частичный остаток удвоится, к нему прибавится делитель B,и на сумматоре сформируется число 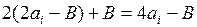 .Аналогичный остаток может быть сформирован на сумматоре в случае пропуска операции вычитания делителя в
.Аналогичный остаток может быть сформирован на сумматоре в случае пропуска операции вычитания делителя в 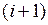 -м цикле. Действительно, в результате двух сдвигов влево на один разряд остаток
-м цикле. Действительно, в результате двух сдвигов влево на один разряд остаток 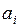 будет умножен на 4, а поскольку он положительный, то в
будет умножен на 4, а поскольку он положительный, то в 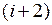 -м цикле из него следует вычесть делитель. Для случая
-м цикле из него следует вычесть делитель. Для случая 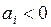 рассуждения аналогичны.
рассуждения аналогичны.
Таким образом, если удвоенный частичный остаток содержит в знаковом и старшем после запятой разрядах двоичную комбинацию «0,0», то во втором такте арифметическая операция не выполняется и очередная цифра частного формируется равной знаковому разряду сумматора, т.е. нулю. Если удвоенный частичный остаток содержит в знаковом и старшем после запятой разрядах двоичную комбинацию «1,1», то во втором такте арифметическая операция также не выполняется и очередная цифра частного равна единице. В случае несовпадения разрядов справа и слева от запятой требуется выполнение арифметической операции.
Пример.
[А]пр = 0,101001;
[В]пр = 0,110011;
С = А/В.
1. Определение знака частного.
ЗнС = ЗнА Å ЗнВ = 0 Å 0 = 0.
2. Деление мантисс.
Частное Делитель
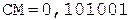
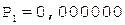
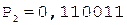
 0.
0. 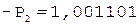
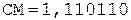 < 0, деление без переполнения
< 0, деление без переполнения
1. 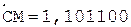
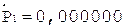
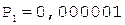
2. 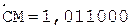
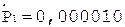


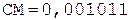
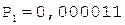
3. 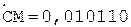
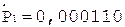
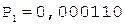
4. 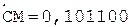
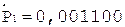

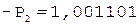
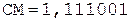
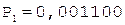
5. 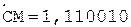
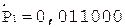
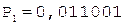
6. 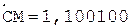
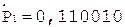
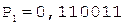
Таким образом, частное C = 0,110011.
Описанный метод позволяет ускорить выполнение операции деления только в тех циклах, в которых остаток денормализован, а в остальных циклах деление происходит по неускоренному алгоритму. Поэтому в худшем случае, при постоянном формировании нормализованного остатка, этот метод не дает прироста производительности.
Рассмотрим еще один метод ускорения выполнения операции деления, основанный на анализе двух разрядов очередного частичного остатка, при котором арифметическая операция может быть пропущена, если абсолютное значение удвоенного частичного остатка меньше делителя. В противном случае требуется выполнение арифметической операции, определяемой знаком сумматора. Поскольку в результате удвоения очередного частичного остатка может произойти переполнение сумматора, необходимо использовать модифицированный код. При переполнении сумматора содержащееся в нем число по модулю больше единицы, т.е. заведомо больше делителя, поэтому также следует выполнять арифметическую операцию, определяемую старшим знаковым разрядом сумматора.
В табл. 2.5 приведены различные сочетания пар старших разрядов регистра делителя и сумматора.
Таблица 2.5
| Старшие разряды сумматора | Старшие разряды модуля делителя | |
| 0,10 | 0,11 | |
| 0,00 1,11 | Арифм. операция не выполняется | Арифм. операция не выполняется |
| 0,01 1,10 | Арифм. операция не выполняется | Арифм. операция не выполняется |
| 0,10 1,01 | Требуется арифм. операция | Арифм. операция не выполняется |
| 0,11 1,00 | Требуется арифм. операция | Требуется арифм. операция |
Пример.
Разделим мантиссы чисел из предыдущего примера. Частное, формируемое в первом регистре, в обоих случаях должно совпадать.
Частное Делитель
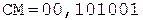
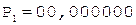
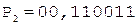
 0.
0. 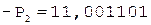
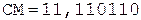 < 0, деление без переполнения
< 0, деление без переполнения
1. 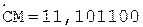
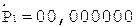
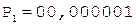
2. 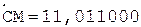
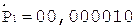
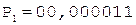
3. 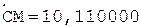
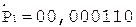


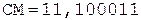
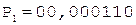
(окончание примера на следующей странице)
4. 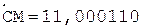
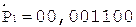


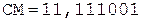
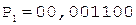
5. 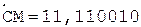
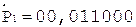
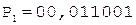
6. 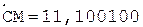
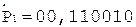
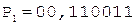
Дата добавления: 2020-02-05; просмотров: 835;











