Умножение инверсных кодов чисел
Выполнение умножения инверсных кодов чисел аналогично умножению прямых кодов, но с некоторыми отличиями. Во-первых, при использовании модифицированного сдвига (сохраняющего знак сумматора или регистра множимого) знак произведения формируется автоматически. Во-вторых, при отрицательном множителе необходима коррекция произведения.
Коррекция произведения выполняется следующим образом. Пусть отрицательный множитель B задан в инверсном коде. Тогда в его цифровых разрядах (разрядах после запятой) содержатся величины 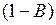 или
или 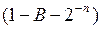 для дополнительного и обратного кода соответственно. В результате выполнения n циклов умножения на сумматоре в случае дополнительного кода будет сформировано произведение
для дополнительного и обратного кода соответственно. В результате выполнения n циклов умножения на сумматоре в случае дополнительного кода будет сформировано произведение 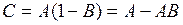 , а в случае обратного кода
, а в случае обратного кода 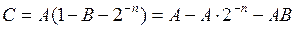 . В обоих случаях истинное произведение представляет собой (
. В обоих случаях истинное произведение представляет собой ( 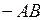 ).
).
Для выполнения коррекции при использовании обратного кода к содержимому сумматора после умножения необходимо прибавить сначала 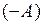 , а в следующем такте
, а в следующем такте 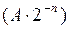 . При умножении младшими разрядами вперед поправка
. При умножении младшими разрядами вперед поправка 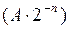 может быть заменена прибавлением величины
может быть заменена прибавлением величины 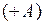 перед выполнением умножения, а поправка
перед выполнением умножения, а поправка 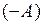 делается после умножения. При умножении обратных кодов чисел старшими разрядами вперед поправка
делается после умножения. При умножении обратных кодов чисел старшими разрядами вперед поправка 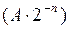 после выполнения n циклов умножения автоматически образуется в регистре множимого и ее необходимо прибавить к сумматору, а поправка
после выполнения n циклов умножения автоматически образуется в регистре множимого и ее необходимо прибавить к сумматору, а поправка 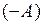 делается перед началом выполнения умножения, поэтому в рассматриваемом случае для коррекции произведения перед выполнением умножения из сумматора вычитается содержимое регистра множимого (прибавляется
делается перед началом выполнения умножения, поэтому в рассматриваемом случае для коррекции произведения перед выполнением умножения из сумматора вычитается содержимое регистра множимого (прибавляется 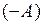 ), а после выполнения n циклов умножения содержимое регистра множимого снова прибавляется к содержимому сумматора, но без изменения знака.
), а после выполнения n циклов умножения содержимое регистра множимого снова прибавляется к содержимому сумматора, но без изменения знака.
Коррекция произведения дополнительных кодов чисел при умножении младшими разрядами вперед (неподвижное множимое) осуществляется путем вычитания содержимого регистра множимого из сумматора после выполнения n циклов умножения. При умножении старшими разрядами вперед необходимо вычитать из содержимого сумматора множимое (прибавлять 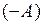 ) до начала выполнения умножения.
) до начала выполнения умножения.
Сказанное можно компактно представить в виде табл. 2.4.
Таблица 2.4
| В обратном коде | В дополнительном коде | ||
| мл. разрядами | ст. разрядами | мл. разрядами | ст. разрядами |
1. 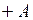
| 1. 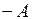
| 1. Умножение | 1. 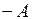
|
| 2. Умножение | 2. Умножение | 2. 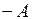
| 2. Умножение |
3. 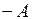
| 3. 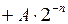 (сдвинутое на n разрядов содержимое регистра множимого)
(сдвинутое на n разрядов содержимое регистра множимого)
|
Пример.
Умножение младшими разрядами вперед.
[А]д = 0,110001;
[В]д = 1,011011;
С = А ´ В.

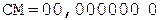
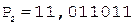
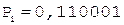
 1. +
1. + 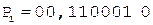
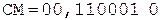
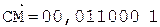
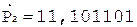
 2. +
2. + 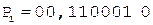
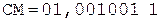
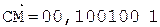
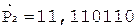
3. 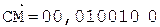
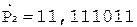
 4. +
4. + 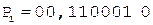
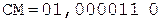
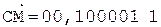
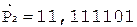
5. + 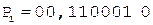

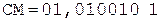
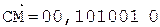
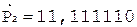
6. 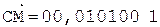
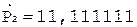
7. – 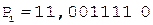

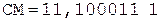
 Окр. +
Окр. + 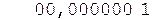
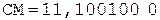
Таким образом, ограничивая результат шестью разрядами, получим:
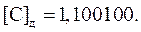
Это число денормализовано, поэтому в случае умножения с плавающей запятой необходимо выполнить нормализацию.
В прямом коде результат умножения запишется следующим образом: 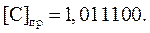
Дата добавления: 2020-02-05; просмотров: 860;











