Извлечение квадратного корня
Операция извлечения квадратного корня включается в совокупность арифметических операций ЭВМ в том случае, когда она составляет не менее 2 % от общего числа операций или является составной частью специализированных алгоритмов, выполняемых с высоким быстродействием. В противном случае квадратный корень можно извлекать итеративно, например, по формуле Герона.
Процедура извлечения квадратного корня сводится к процедуре деления, при этом делитель в каждом цикле формируется из полученных на предыдущем этапе цифр частного путем приписывания к частному некоторой двоичной комбинации.
В общем случае извлечение квадратного корня из числа, представленного с плавающей запятой, осуществляется в два этапа. На первом этапе формируется порядок результата, а на втором – мантисса.
Для определения порядка результата порядок исходного операнда следует разделить на 2. Если порядок подкоренного числа четный, то деление на 2 выполняется путем сдвига его кода вправо на один двоичный разряд (отрицательный порядок должен быть представлен инверсным кодом). Если порядок нечетный, то перед делением на 2 его значение следует увеличить на единицу, что повлечет за собой необходимость денормализовать мантиссу. Таким образом, при нечетном порядке к его значению в первом такте прибавляют 1, а во втором такте одновременно сдвигают мантиссу и увеличенное значение порядка на один разряд вправо. При четном или нечетном порядке операнда результат выполнения операции все равно будет получаться нормализованным.
Как и в случае деления, квадратный корень можно извлекать с восстановлением и без восстановления остатка. При этом результат всегда будет получаться с недостачей, поэтому необходимо вычислять дополнительную цифру и производить округление.
Рассмотрим сначала метод извлечения квадратного корня с восстановлением остатка.
Для получения 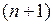 цифр корня следует выполнить
цифр корня следует выполнить 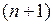 циклов, каждый из которых распадается на три такта. В первом такте из содержимого сумматора, т.е. из очередного частичного остатка, вычитается делитель, сформированный из уже полученных цифр частного и приписки «01». Очевидно, что в первом цикле делитель представляет собой число «0,01». Во втором такте в случае отрицательного сумматора требуется процедура восстановления остатка путем прибавления к сумматору положительного делителя. В третьем такте формируется очередная (начиная со старшей) цифра корня, равная нулю, если в первом такте сумматор оказался отрицательным, или единице, если в первом такте сумматор оказался положительным. В этом же такте выполняется сдвиг очередного частичного остатка на один разряд влево. По окончании выполнения операции производится округление результата.
циклов, каждый из которых распадается на три такта. В первом такте из содержимого сумматора, т.е. из очередного частичного остатка, вычитается делитель, сформированный из уже полученных цифр частного и приписки «01». Очевидно, что в первом цикле делитель представляет собой число «0,01». Во втором такте в случае отрицательного сумматора требуется процедура восстановления остатка путем прибавления к сумматору положительного делителя. В третьем такте формируется очередная (начиная со старшей) цифра корня, равная нулю, если в первом такте сумматор оказался отрицательным, или единице, если в первом такте сумматор оказался положительным. В этом же такте выполняется сдвиг очередного частичного остатка на один разряд влево. По окончании выполнения операции производится округление результата.
Пример.
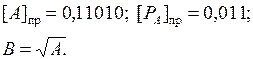
1. Определение порядка результата.
PB = PA/2:
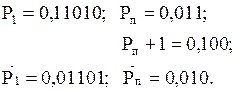
Таким образом, порядок результата PB = 0,010.
2. Определение мантиссы.
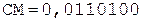
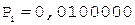
 1. -
1. - 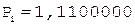
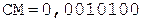
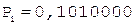
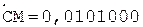
 2. -
2. - 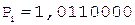
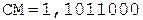
 +
+ 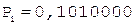
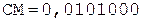
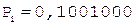
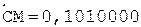
 3. -
3. - 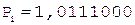
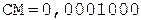
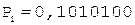
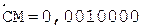
 4. -
4. - 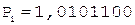
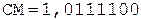
 +
+ 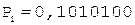
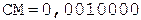
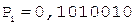
(окончание примера на следующей странице)
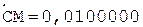
 5. -
5. - 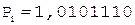
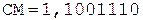
 +
+ 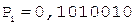
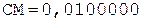
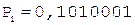
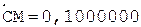
 6. -
6. - 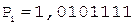
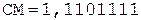
 +
+ 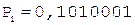
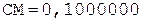
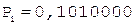
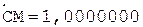
Окр. 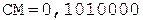
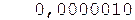

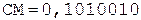
Окончательно 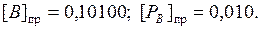
Извлечение квадратного корня без восстановления остатка является модификацией предыдущего алгоритма. В каждом цикле выполняются два такта. В первом такте в зависимости от знака сумматора выполняется арифметическая операция. Если сумматор положительный, то из него вычитается делитель. Если сумматор отрицательный, то, наоборот, к нему прибавляется положительный делитель. Во втором такте анализируется знак очередного остатка. Если остаток положительный, то очередная цифра частного – единица и приписка к частному для формирования делителя «01». В противном случае очередная цифра частного – нуль и приписка к частному для формирования делителя «11». Одновременно с формированием частного и переменного делителя выполняется удвоение очередного частичного остатка. При этом знаковый разряд может быть искажен, поэтому для сохранения знака следует использовать модифицированный код.
Пример.
Рассмотрим число из предыдущего примера.
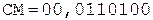
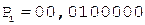
 1. -
1. - 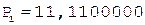
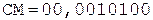
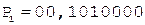
(окончание примера на следующей странице)
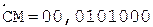
 2. -
2. - 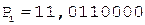
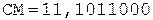
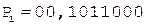
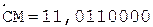
 3. +
3. + 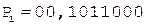
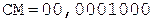
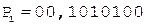
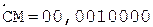
 4. -
4. - 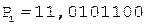
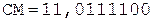
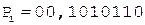
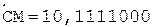
5. + 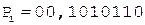

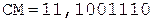
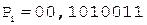
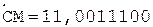
 6. +
6. + 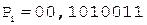
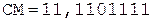
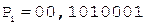
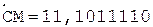
Окр. 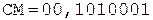

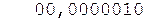
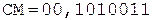
Окончательно 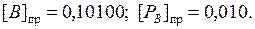
2.7. Выполнение арифметических операций
в D-кодах
О представлении чисел двоично-десятичными кодами см. в разделах 1.1 и 1.5.
Сложение в D-кодах
Вначале рассмотрим сложение чисел в D-коде 8421.
Выполнение операции сложения в D-коде 8421 имеет ряд особенностей: во-первых, возникающий при сложении межтетрадный перенос вместо необходимых десяти единиц (как это принято в десятичной системе счисления при формировании переноса в следующий разряд) уносит шестнадцать (16 – удвоенный вес старшего разряда тетрады), т.е. значение, содержащееся в тетраде, из которой возник перенос, на шесть единиц меньше необходимого; во-вторых, при сложении тетрад могут получаться запрещенные комбинации, соответствующие числам больше девяти, но меньше пятнадцати; в-третьих, отрицательные числа необходимо представлять в инверсном коде, но, как указывалось выше, D-код 8421 не обладает свойством самодополняемости, что необходимо учитывать.
Все указанные трудности решаются путем прибавления тетрады 0110, соответствующей коду цифры 6. Действительно, если межтетрадный перенос уменьшает значение в тетраде на шесть лишних единиц, то коррекция может быть осуществлена путем прибавления недостающих шести единиц. Далее, для коррекции тетрад, содержащих запрещенные комбинации, из них, очевидно, необходимо вычесть 10. Вычитание 10-ти можно заменить прибавлением дополнения 10-ти до 16-ти, т.е. для коррекции к значению запрещенной комбинации следует прибавить 6. Для получения обратного кода все тетрады числа (кроме знака) необходимо сначала увеличить на 6, а затем поразрядно инвертировать. Дополнительный код может быть получен из обратного путем прибавления единицы к младшему разряду младшей тетрады числа.
Рассмотрим пример.
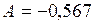 ;
; 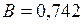 ;
;
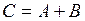 .
.
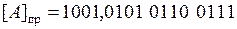 ;
;
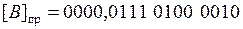 .
.
Поскольку первое слагаемое отрицательное, его необходимо представить в инверсном коде, например, дополнительном.
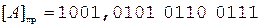
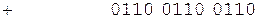

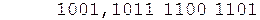
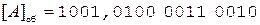
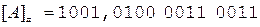
Так как дополнительный код положительного слагаемого совпадает с его прямым кодом, переходим непосредственно к сложению.
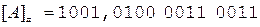

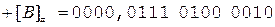
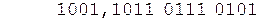

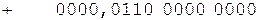 Коррекция
Коррекция
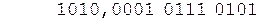

 Коррекция (нули опустим)
Коррекция (нули опустим)
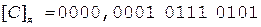
Таким образом, 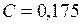 .
.
При выполнении сложения в D-коде 8421+3 обратный код отрицательного операнда может быть получен путем инвертирования двоичных разрядов кода (дополнительный код получается из обратного прибавлением единицы к младшему разряду).
После сложения операндов необходимо всегда выполнять коррекцию результата. Легко видеть, что если при сложении из тетрады не было переноса, то ее значение следует уменьшить на три единицы (вычесть 0011), а если перенос был, то увеличить на три единицы (прибавить 0011). Очевидно, вычитание 0011 можно заменить прибавлением дополнения 3 до 16, т.е. для коррекции к тетрадам, из которых при сложении не возник перенос, необходимо прибавить 1101. Следует помнить, что при выполнении коррекции в D-коде 8421+3 переносы между тетрадами не распространяются.
Рассмотрим пример. Значения слагаемых возьмем из предыдущего примера.
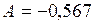 ;
; 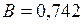 ;
;
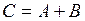 .
.
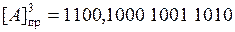 ;
;
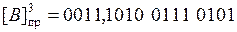 .
.
Получим дополнительный код первого операнда вышеописанным способом и выполним сложение.
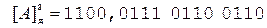

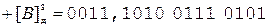

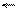
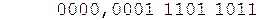 (переносы показаны стрелками)
(переносы показаны стрелками)
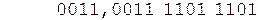 Коррекция (без переносов)
Коррекция (без переносов)

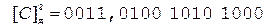
Таким образом, 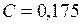 .
.
В дальнейшем будем рассматривать выполнение арифметических операций в D-коде 8421+3.
Дата добавления: 2020-02-05; просмотров: 1094;











