Вопрос 1. Принятие наиболее эффективного инвестиционного решения.
У начинающих предпринимателей или у действующих предприятий в процессе их расширения или технического перевооружения и диверсификации производства возникает проблема сферы приложения инвестируемых средств. Принятие наиболее эффективного инвестиционного решения основано на процедурах наращения и дисконтирования. Рассмотрим сущность этих процедур. Предположим, что инвестор имеет некоторую сумму X и решил вложить ее в банк со ставкой процента по вкладам Z, тогда сумма вклада к концу первого года F1 составит: F1=x+xz. В данном выражении Z уже не в процентах, а долях единицы, т.е. 10%=0,1, 20%=0,2 и т.д. К концу второго года сумма вклада составит
F2=x+xz+(x+xz)z= x+xz+ xz+ xz2= x+2xz+ z2= x(1+2 z+ z2)=x(1+ z)2. [7, стр.161]
Определив сумму вклада к концу третьего года по этой же схеме получим F3=x(1+z)3. Таким образом, приходим к выводу, что Fn=x(1+z)n. По этой формуле можно определить наращенную к концу любого периода сумму. Сомножитель (1+z) называется факторным множителем и для облегчения расчетов значения факторного множителя приводятся в экономической литературе в виде матрицы в зависимости от значения z и номера периода п. При решении задач по определению эффективности инвестиционного решения параметр z принято называть нормой дисконта, в качестве которой выступает ставка процента по вкладам, среднеотраслевая норма отдачи на вложенный капитал или желаемая для инвестора норма отдачи на вложенный капитал. Из выражения Fn=x(l+z)n можно определить текущую стоимость будущей суммы, получаемой в виде наращенной суммы банковского вклада или в виде прибыли от реализованного инвестиционного проекта. Процедура определения текущей стоимости будущей суммы называется дисконтированием. Дисконтирование - это процедура обратная процедуре наращения, т.е.
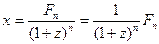 [7, стр.166]
[7, стр.166]
Сомножитель 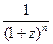 называется коэффициентом дисконтирования. Коэффициенты дисконтирования также приводятся в виде матрицы в зависимости от нормы дисконта z и норма периода n.
называется коэффициентом дисконтирования. Коэффициенты дисконтирования также приводятся в виде матрицы в зависимости от нормы дисконта z и норма периода n.
Рассмотрим принятие наиболее эффективного инвестиционного решения на основе процедур наращения и дисконтирования на конкретном примере. Предположим, что предприниматель рассматривает три варианта инвестиционного решения. Данные о распределении капитальных вложений по годам и предполагаемые суммы денежного потока в виде прибыли приведены в таблице 1 при норме дисконта (банковском проценте по вкладам, среднеотраслевой норме отдачи па вложенный капитал или желаемая норма отдачи) - 10%,
Таблица 1
В млн. рублях
| Инвестиции по годам | Всего | Сумма денежного в течение жизни проекта | ||||||||
| 2008 год пуска | ||||||||||
| Мвл | Мn | Мвл | Мn | Мвл | Мn | Мвл | Мn | Мвл | Мn | |
| 5 | Ежегодно 2 млн. и течение 10 лет | |||||||||
| Ежегодно 3 млн. в течение 10 лет | ||||||||||
| Ежегодно 5 млн. в течение 15 лет |
В таблице Мвл - это вложенная в данном году номинальная сумма капитальных вложений Мn это наращенная к моменту пуска сумма капитальных вложений. В графе «всего» приводится общая (номинальная) сумма капитальных вложений и общая наращенная к моменту пуска сумма капитальных вложений. Следует учесть, что капитальные вложения в год пуска не наращиваются, т.е. Мвл=Мn.
Наиболее эффективный вариант вложения определяется по так называемому критерию чистой дисконтированной стоимости - NPV (аббревиатура названия данного критерия на английском языке). Критерий чистой дисконтированной стоимости определяется как разница между дисконтированной суммой денежного потока и наращенной к моменту пуска общей суммой капитальных вложений, т.е.
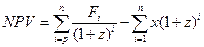
Если NPV>0 - проект эффективности, NPV=0 - проект ни убыточный и не эффективный, NPV <0— проект убыточный (неэффективный).
Дата добавления: 2016-06-15; просмотров: 2101;











