Распределение местных осредненных скоростей.
Это распределение можно получить из (3) с учетом зависимости (2):
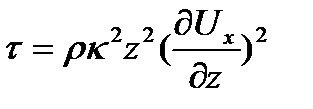 ,
,
где z- расстояние точки от стенки трубы.
Принимая осредненное (первичное) движение установившимся и плавно изменяющимся, запишем
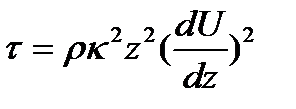 или
или
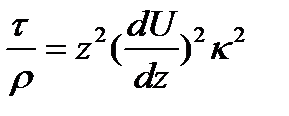 .
.
Выражение 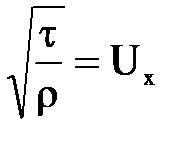 имеет размерность скорости, которую называют динамической.
имеет размерность скорости, которую называют динамической.
Тогда 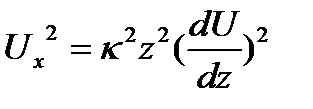 , или
, или 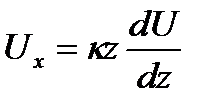
Разделяя переменные получим
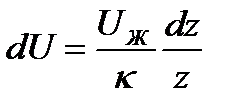 .
.
Интегрируя, с учетом, что 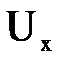 и κ постоянные получим
и κ постоянные получим
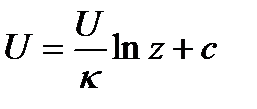
Постоянную интегрирования С определяем из начальных условий. Для трубы max осредненная скорость 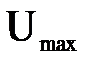 находится в ее центре, то есть при
находится в ее центре, то есть при 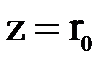 .
.
Тогда С=Uмах – Uж/κ ln rо,
или U=Uж/κ ln z + Umax- Uж/κ ln ro
и окончательно
U=Umax-Uж/κ ln(ro/z)
Таким образом, в ядре развитого турбулентного потока местные осредненные скорости изменяются по логарифмическому закону, что подтверждается экспериментально.
Эпюра характеризуется тем, что скорости на поверхности стенки трубы равны нулю, вследствие прилипания частиц жидкости; на весьма малом расстоянии от стенок (в прастеночном слое) скорости достигают значительной величины, мало отличающиеся от значений скорости в других точках живого сечения потока, поэтому наибольшие градиенты скорости наблюдаются у стенок; в точках живого сечения, более отдаленных от поверхности стенок, скорости изменяются относительно мало, и поэтому мал и градиент скорости; более равномерное движение можно объяснить турбулентным перемешиванием (переносом) частиц жидкости. Коэффициент кинетической энергии при турбулентном режиме движения принимается 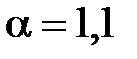 . Иногда его приближенно принимают
. Иногда его приближенно принимают 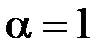 в отличие от ламинарного режима, где
в отличие от ламинарного режима, где 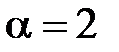 .
.
Дата добавления: 2016-06-15; просмотров: 1782;











