Шероховатость стенок.

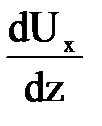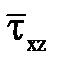Как показывают исследования, вблизи стенки имеет место 80-90% общего количества потерь энергии от молекулярной вязкости. Это обусловлено тем, что на сравнительно малом расстоянии скорость изменяется от нуля у стенки до конечных значений, близких к средней скорости. Слой жидкости, в пределах которого и являются еще ощутимыми называют пристеночным. За его пределами, в соответствии с гипотезой Прандтля, вязкость жидкости можно вовсе не учитываться, то есть можно считать ее идеальной. Анализ движения потока в пристеночном слое указывает на то, что потери энергии зависят от состояния стенки-степени ее шероховатости. В зависимости от соотношения между толщиной вязкого подслоя 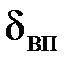и средней высотой выступов шероховатости Δ различают следующие виды поверхности. Если толщина вязкого подслоя 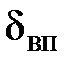больше абсолютной высоты выступов шероховатости, то такие поверхности называются гидравлическигладкими. В этом случае выступы шероховатости покрываются вязким подслоем, и потери энергии по длине практически не зависят от шероховатости стенок. Если толщина 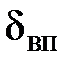меньше высоты , то поверхности называют гидравлически шероховатыми.

Поверхность стенок труб, каналов или естественных русел не является абсолютно гладкой- она шероховата, при этом характер шероховатости может быть различным: шероховатость бывает либо волнистой, либо зубчатой.

Абсолютной шероховатостью стенок трубы называют среднюю высоту выступов шероховатости. Величина абсолютной шероховатости обозначается буквой ; она зависит от материала труб и технологии их изготовления. Если величина абсолютной шероховатости для различных точек стенок трубы различна, то такую шероховатость называют неоднородной шероховатостью. Чтобы упростить изучение движения потока, неоднородную шероховатость заменяют величиной однородной абсолютной шероховатостью и эквивалентной ей по потерям напора. Величину эту обозначают .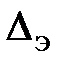

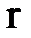Отношение величины абсолютной шероховатости к величине радиуса или диаметра d трубы называют относительной шероховатостью и обозначают 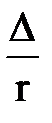или .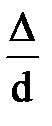

При таких поверхностях обтекание выступов шероховатости происходит с отрывом от них. Если 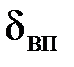соизмеримо с то такие поверхности называют переходными. Толщину вязкого подслоя 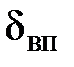можно определить из условия, что турбулентные касательные напряжения в нем пренебрежительно малы по сравнению с вязкими напряжениями. В этом случае 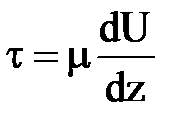. Если принять 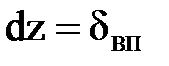, то 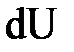будет равно предельной скорости на границе вязкого подслоя, 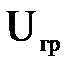, так как скорость на стенке равна нулю.

Следовательно,

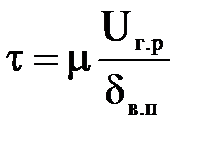, или

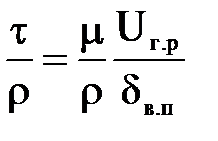(4)

Используя понятие динамической скорости ,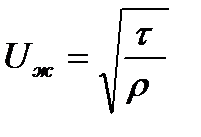

и вводя кинематическую вязкость 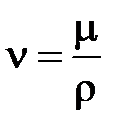в (4),

получим ,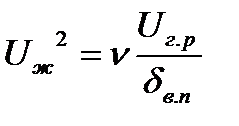

откуда толщина вязкого подслоя .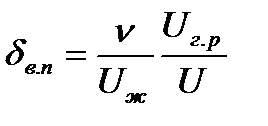

Отношение 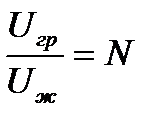является постоянным и называется числом Никурадзе (обычно )

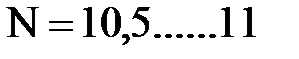Учитывая число Никурадзе, можно записать 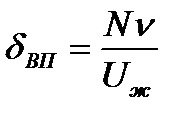(5)

Толщина вязкого подслоя 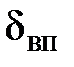не постоянна и зависит от числа Рейнольдса. Разделим левую и правую части зависимости (5) на линейный размер, например на диаметр d, и получим 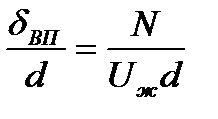, но

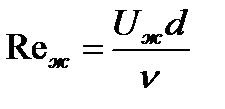и тогда .

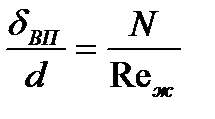Величина Re_ж характеризуется динамической скоростью U_ж.

При возрастании средней скорости турбулентности потока увеличиваются касательные напряжения 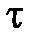и поэтому возрастают значения динамической скорости 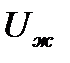и соответственно величина Re_ж. Толщина вязкого подслоя 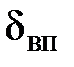уменьшается с возрастанием числа Рейнольдса. С увеличением скорости турбулентного потока толщина 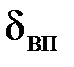может уменьшиться настолько, что выступы шероховатости «прорежут» этот вязкий подслой. Тогда движение потока будет происходить уже а переходной зоне, в которой сопротивление движению жидкости еще зависят от числа Re, но уже начинает сказываться и влияние высоты выступов шероховатости .

При дальнейшим увеличении Re толщина 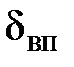еще больше уменьшается (теоретически даже может исчезнуть) и вязкий подслой не оказывает влияние на сопротивления, так как движение происходит по шероховатой поверхности. В этом случае потери зависят от числа Re, то есть наступает состояние полностью развитой турбулентности.

Понятия гладкой и шероховатой поверхности относительные, так как одна и та же поверхность при малых числах Re будет гидравлически гладкой, а при больших- уже гидравлически шероховатой.

Лекция 11. Экспериментальный график Никурадзе. Потери на трение для промышленных труб. Универсальная приближенная формула.