МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ.

При движении реальной жидкости помимо потерь на трение по длине потока, могут возникать и так называемые местные потери напора. Причиной последних в трубопроводах являются разного рода конструктивные вставки (колена, тройники, сужения и расширения трубопровода, задвижки, вентили и др.). Местные сопротивления вызывают изменение скорости движения жидкости по значению (сужение и расширение), направлению (колено) или по значению и направлению одновременно (тройник).

Поэтому часто указывают на некоторую аналогию между явлениями, наблюдаемыми в местных сопротивлениях, и ударом в твердых телах, который с механической точки зрения так же характеризуется внезапным изменением скорости.

В практических расчетах местные потери определяют по формуле, выражающей потерю пропорционально скоростному напору.

,

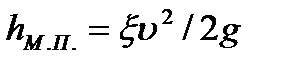где 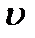- средняя скорость движения жидкости в сечении потока за местным сопротивлением;

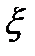- безразмерный коэффициент, называемый коэффициентом местного сопротивления. Значение 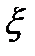устанавливают опытным путем.

Если по каким-либо соображениям потерю напора желательно выразить через скорость перед местным сопротивлением, необходимо выполнить перерасчет коэффициента местного сопротивления. Для этой цели можно воспользоваться соотношением

,

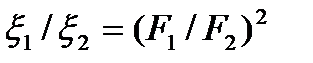где 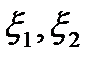- коэффициенты местных сопротивлений, соответствующие сечениям .

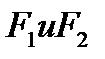В некоторых случаях, оказывается удобным определять местные потери по так называемой эквивалентной длине, длине прямого участка трубопровода данного диаметра, на котором потери напора на трение по длине 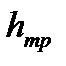равны (эквивалентны) потерям напора 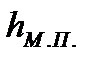, вызываемым соответствующим местным сопротивлением. Эквивалентная длина 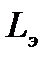может быть найдена из равенства потерь напора по длине, определяемой по формуле Дарси – Вейзбаха 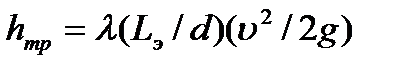и местных потерь напора, учитываемых формулой .

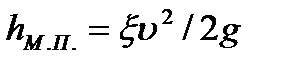Приравнивая правые части этих формул находим:

.

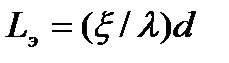Если рассмотреть наиболее характерный случай местного сопротивления в виде внезапного расширения трубопровода, когда поперечное сечение резко увеличивается от F₁ и F₂, можно наблюдать следующую картину. Частицы жидкости пройдя сечение 1-1 с некоторой скоростью стремятся двигаться дальше в том же направлении с той же скоростью.

Однако они задерживаются частицами, находящимися впереди и обладающими (ввиду увеличения сечения) меньшими скоростями, как бы наталкиваются и ударяются о них, и поэтому получают смещение в поперечном направлении, что вызывает расширение струи. В некотором сечении , находящемся на небольшом расстоянии от первого сечения, поток жидкости заполняет все сечение трубы. При этом, в начале трубы большего диаметра в углах образуется вихревая область, представляющая собой кольцевое пространство, заполненное жидкостью, не участвующей в основном поступательном движении в направлении оси трубопровода. По причине трения на граничных поверхностях, эта жидкость находится здесь во вращательном, вихревом движении, вызывающем значительные потери энергии.

Аналогичные явления имеются при движении жидкости в колене, где также образуются вихревые области, и во всех других случаях местных сопротивлений.

Теоретическое определение местных потерь напора представляет значительные трудности ввиду большой сложности происходящих при этом процессов, и может быть выполнено лишь для немногих случаев, в частности для внезапного расширения трубопровода.

Рассмотрим решение этой задачи. Для этого в горизонтальном потоке жидкости выделим объем между сечениями 1-1 и 2-2 и применим к нему теорему о приращении количества движения, согласно которой, приращение количества движения равняется импульсу проекций всех действующих сил на направление движения.

Указанный объем за некоторое время переместится в новое положение, ограниченное сечениями 1’-1’ и 2’-2’. Чтобы определить приращение количества движения, достаточно рассмотреть массу жидкости объемов между сечениями

1-1, 1’-1’ и 2-2, 2’-2’, поскольку количество движения объемов между сечениями 1-1 и 2-2 остается неизменным.

При этом для искомого приращения количества, движения получим

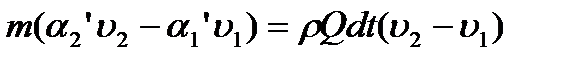(1)

где Q- расход жидкости;

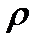- ее плотность;

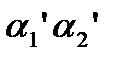- коэффициенты Буссинеска, представляющие собой поправки к количествам движения за счет неравномерности распределения скоростей в поперечных сечениях потока; в дальнейшем будем считать, что эти коэффициенты в обоих сечениях одинаковы и равны единице.

При определении суммы проекций импульсов действующих сил следует учесть, что такими силами являются здесь лишь силы давления на концевые сечения, ограничивающие рассматриваемый объем.

Имея в виду, что гидродинамические давления Р₁ и Р₂ в указанных сечениях равномерно распределены по всей площади F₂ , для этих сил получим:

; .

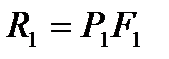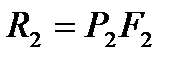Силами трения ввиду малой длины участка растекания 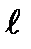можно пренебречь, таким образом, сумма проекций импульсов сил на направление движения (т.е. на ось потока) будет равна

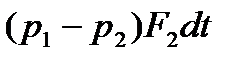(2)

Приравнивая затем выражения (1) и (2) на основании теоремы о приращении количества движения, получим

.

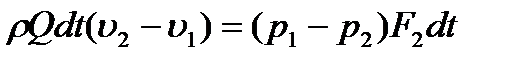Последнее выражение после деления на 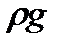и замены 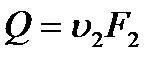примет вид:

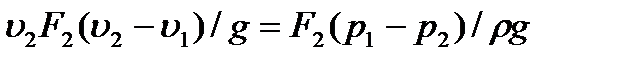
или .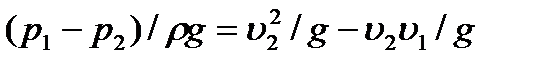

Составим далее для тех же двух сечений, имея в виду сделанные выше допущения, уравнение Бернулли в его обычной форме, из которого легко найдем следующее выражение для потери напора при внезапном расширении:

.

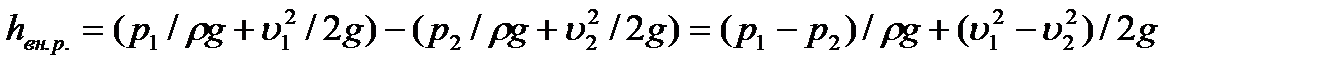Преобразуем это выражение и подставим в него вместо 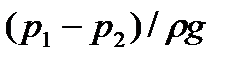установленное ранее его значение (в). Получим

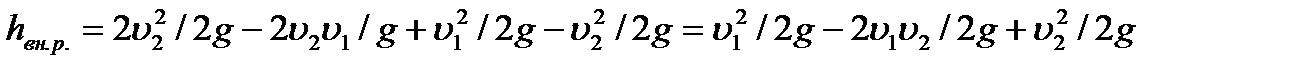
или окончательно 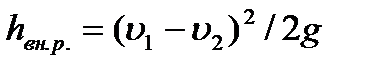(3)

т.е. потеря напора при внезапном расширении равна скоростному напору, соответствующему потерянной скорости 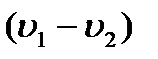. Этот результат известен под названием теоремы или формулы Борда и хорошо подтверждается опытными данными при турбулентном режиме.