Касательные напряжения в турбулентном потоке.
Движение жидкости при турбулентном режиме всегда должно происходить со значительно большей затратой энергии, чем при ламинарном, так как энергия затрачивается не только на преодоление вязких напряжений, но и тех дополнительных, которые характерны для турбулентного потока и связаны с преодолением сопротивлений пульсации скорости. Явление перехода энергии движения в тепло называют диссипацией энергии. Диссипация увеличивается при приближении от центра ядра турбулентности, в пристеночном слое наблюдается зона max диссипации энергии.
Если учитывать, что действие вязкости единственная причина преобразования энергии потока в тепло, то можно объяснить и увеличение количества рассеянной энергии при возрастании турбулентности. Это объясняется тем, что каждый их вихрей в каждый момент времени сам становится источником дополнительного вязкого напряжения, это явление носит название вихревой вязкости.
Наличие вихрей разных размеров приводит к тому, что появляются дополнительные так называемые турбулентные касательные напряжения, обусловленные самой природой движения . Ж. Буссинеск ввел специальное понятие коэффициента молярной (вихревой) вязкости, с помощью которого можно выразить это добавочное напряжение от пульсации в функции от среднего градиента скорости.
С учетом этого можно записать, что в общем случае для турбулентного режима движения
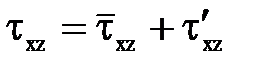 и соответственно
и соответственно
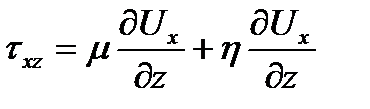 , где
, где
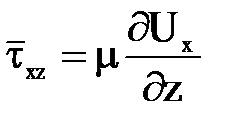 и
и 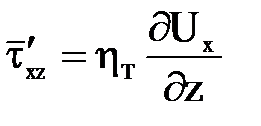 .
.
Величина 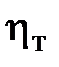 называется динамической турбулентной вязкостью, а ее размерность такая же, как у динамической (молекулярной) вязкости μ, которая зависит от рода жидкости. Значение
называется динамической турбулентной вязкостью, а ее размерность такая же, как у динамической (молекулярной) вязкости μ, которая зависит от рода жидкости. Значение 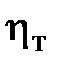 выражает вихревую (молярную) вязкость и зависит от характера движения. Динамической турбулентной вязкости так же соответствует кинематическая турбулентная вязкость
выражает вихревую (молярную) вязкость и зависит от характера движения. Динамической турбулентной вязкости так же соответствует кинематическая турбулентная вязкость 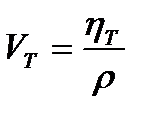 , с учетом которой
, с учетом которой 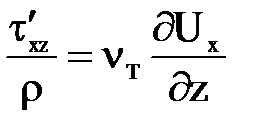 .
.
В 1897 г. Ж. Буссинеск, используя аналогию между турбулентным движением жидкости и тепловым движением молекул газа, принял, что турбулентные касательные напряжения
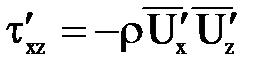 .
.
Тогда 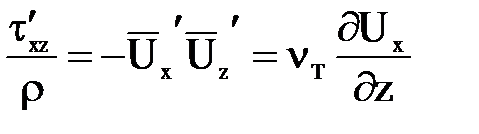 и следовательно
и следовательно 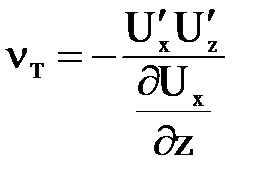 ,
,
то есть кинематическая турбулентная вязкость определяется пульсационными характеристиками, которые выражают природу турбулентного режима движения.
При любом числе Re меньше критического динамическая турбулентная вязкость равна нулю и тогда для ламинарного режима движения
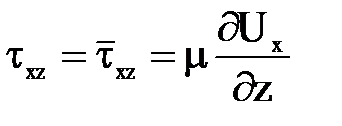 ,
,
то есть потери на трение пропорциональны скорости в первой степени. В вязком подслое турбулентного потока течение обуславливается вязким трением и поэтому для него справедлива эта зависимость.
Для числа Re более критического вихревая вязкость значительно возрастает, а при весьма больших значениях Re (вполне развитое турбулентное движение) она возрастает настолько, что полностью умаляет значение молекулярной вязкости. Другими словами для турбулентного ядра напряжения, вызываемые молекулярной вязкостью и зависящие от градиента осредненной скорости, ничтожны по сравнению с добавочными турбулентными (вихревыми) напряжениями. В связи с этим для полностью развитой турбулентности, можно пренебречь μ и записать 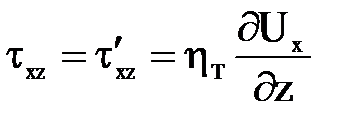 (1)
(1)
Если принять связь между турбулентными характеристиками и скоростью осредненного потока по Л. Прандтлю, то динамическая турбулентная вязкость может быть представлена в виде 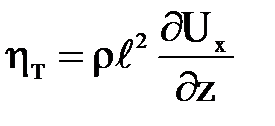 .
.
Величина 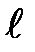 называется длиной пути смешения, или перемешивания под которой понимается проекция на ось
называется длиной пути смешения, или перемешивания под которой понимается проекция на ось 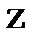 пути, достаточно для того чтобы частицы, попадающие из одного слоя в другой, полностью приобретали его кинематические характеристики. Длина пути смешения
пути, достаточно для того чтобы частицы, попадающие из одного слоя в другой, полностью приобретали его кинематические характеристики. Длина пути смешения 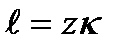 (2)
(2)
где κ - универсальная постоянная Кармана, равная 0,4 для круглой трубы;
z- расстояние от границы (в площади живого сечения) до той точки, где измеряется касательное напряжение.
С учетом значения 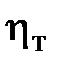 зависимость (1) можно записать
зависимость (1) можно записать
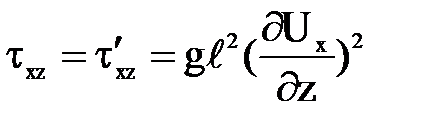 (3)
(3)
Таким образом, потери на трение при турбулентном режиме движения пропорциональны скорости во второй степени.
Для переходной области влияние обоих видов вязкости соизмеримо и поэтому
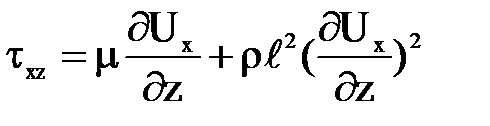 .
.
Дата добавления: 2016-06-15; просмотров: 3284;











