Дифференциальные уравнения равновесия жидкости.

Пусть какое-либо жидкое тело массой М и плотностью 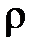находится в равновесии под действием внешних сил, равнодействующая которых F. Будем считать, что координатные оси х и у расположены в горизонтальной плоскости, а ось z направлена вертикально вверх. Разложив силу F на три составляющих, параллельным координатным осям 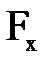, , 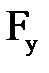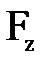и поделив их на m, можно найти ; ; ,

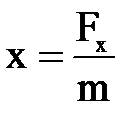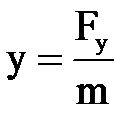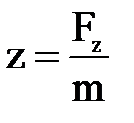где х,у и z-проекции ускорений, вызываемых внешними силами, на соответствующие координатные оси.

Выделим у произвольной точки А в пределах жидкого тела бесконечно малый объем в виде прямоугольного параллелепипеда, грани которого параллельны координатным плоскостям. Мысленно отбросив окружающую выделенный объем жидкость, заменим ее действие силами. Это будут сжимающие силы, нормальные к каждой из плоских граней. 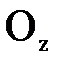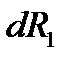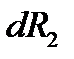Например, в точках 1 и 2 (центры тяжести граней, параллельных плоскости у будут приложены силы и , направленные навстречу друг другу вдоль оси.

Поскольку жидкое тело находиться в покое, то для сил равновесия оси х сил можно записать так: 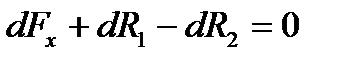(1)

Где 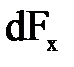-проекция на ось элементарной массовой силы, 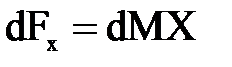из зависимости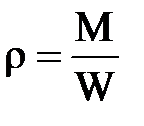

Элементарная масса dM=pdW, где элементарный объем рассматриваемого параллелепипеда dW=dxdydz. Из уравнения 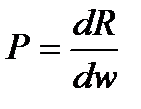, сила гидростатического давления dR=Pdw

то есть ,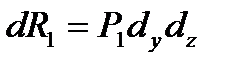

,

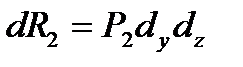Где 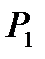и 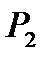-давление в точках 1 и 2.

Считая давление в точке А (центры тяжести рассматриваемого параллелепипеда) равным P, и учитывая, что изменение гидростатического давления, приходящего на единицу длины в направлении координатной оси x, может быть представлено частной производной 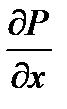, будем иметь ,

.

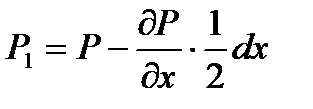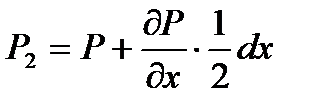Подставляя полученные выражения в начальное уравнение

получим

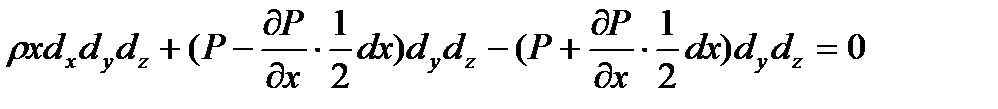(2)

Поскольку 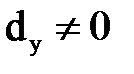и 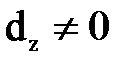, то обе части уравнения можно разделить на 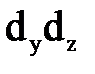, то есть отнести к единице площади

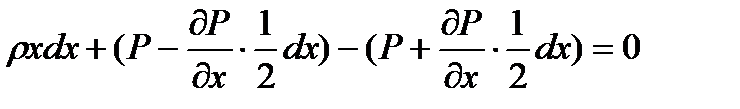
Тогда раскрывая скобки, будем иметь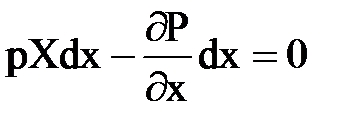

Аналогичным способом с учетом условий равновесия относительно двух других координатных осей получены дифференциальные уравнения подобного вида :

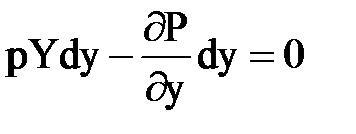
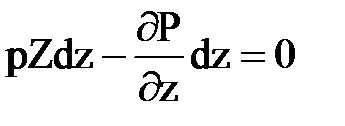
Учитывая, что не только dy и dz, но и dx и p не равны нулю, мы могли бы, как это делается во многих учебниках обе части уравнения разделить на pdxdydz, то есть отнести к единице массы, тогда раскрывая скобки, можно записать

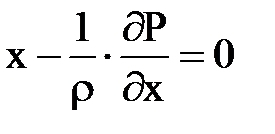
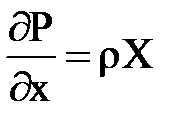
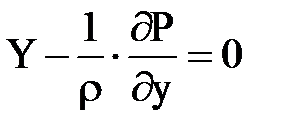
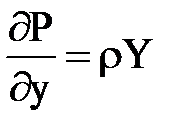
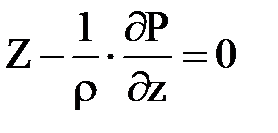
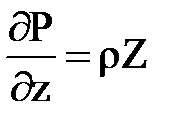
Эти дифференциальные уравнения равновесия жидкого тела были выведены в 1755 г. действительным членом Российской Академии наук Л. Эйлером и носят его имя. Они получены для произвольно заданных сил и позволяют решать всевозможные задачи, связанные с равновесием жидкости.

Сложив почленно все три уравнения получим

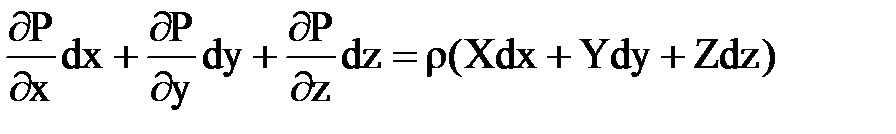
Сумма частных дифференциалов, стоящих в первой части, представляет собой полный дифференциал.

Таким образом,

.

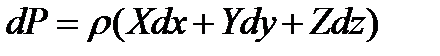Если плотность жидкости 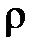с достаточной степенью точности может быть принята постоянной, то гидростатическое давление в любой точке жидкости, находящейся в равновесии под действием внешних сил

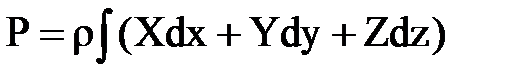
Чтобы это общее выражение использовать для решения тех или иных задач, в каждом конкретном случае необходимо знать ускорение X, Y и Z.

Геометрическое место точек, имеющих одинаковое давление P=const, dP=0,называется поверхностью равного давления или поверхностью уровня.