Лекция № 2. Гидростатика. Свойства гидростатического давления. Дифференциальные уравнения равновесия жидкости. Поверхности уровня. Относительный покой.

Гидростатика-раздел гидравлики, в котором изучается равновесие жидкостей и воздействие покоящихся жидкостей на погруженные в них тела и поверхности, ограничивающие жидкости.

Одна из основных задач гидростатики- изучение распределения давления в жидкости и определение на этой основе сил, действующих со стороны жидкости на соприкасающиеся с ней твердые тела. Значение законов гидростатики позволяет рассчитывать силы, действующие на дно и стенки сосудов различной формы и назначения. На законах гидростатики основано действие гидравлических подъемников, прессов и тормозов, жидкостных манометров и многих других машин, механизмов и приборов.

Жидкость, в том числе и однородная, представляет собой тела, состоящее из расположенных на некотором, хотя и весьма небольшом, расстоянии друг от друга молекул. Однако при решении различных задач гидравлики мы пренебрегаем указанным обстоятельством и рассматриваем жидкость как сплошную среду. Рассматривая жидкость как сплошную среду, мы получаем право говорить о «частицах» жидкости- то есть об элементарных объемах, в которых сосредоточено элементарная масса рассматриваемой жидкости. При этом частицы жидкости, даже бесконечно малые, считают состоящими из большого числа молекул.

Рассмотрим одно из основных понятий - гидростатическое давление. Выделим в жидкости, не находящейся в равновесии, некоторый объем, разделим его произвольной плоскостью АВ на две части и мысленно отбросим одну из них, например, верхнюю. При этом к плоскости АВ мы должны приложить силы, действие которых будет эквивалентно действию отброшенной верхней части объема на оставшуюся нижнюю его часть.

Рассмотрим в плоскости сечения АВ замкнутый контур площадью Δ F, включающим точку а. Пусть на эту площадь действует сила Δ Р.

Отношение 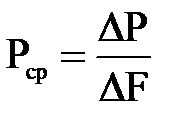представляющее собой силу, действующую на единицу площади, будем называть средним гидростатическим давлением, или средним напряжением гидростатического давления на площади ΔF.

Истинное давление в различных точках этой площади может быть разным; в одних точках оно больше, а в других- меньше среднего гидростатического давления. Очевидно, что в общем случае среднее давление 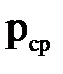будет тем меньше отличаться от истинного в точке а , чем меньшей будет площадь ΔF , и в пределе(при стремлении ее к нулю) среднее гидростатическое давление совпадает в этой точке с истинным.

Таким образом, истинное гидростатическое давление р (обычно называемое просто гидростатическим) будет

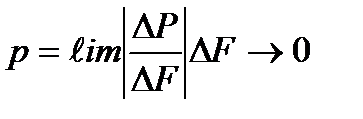
На практике гидростатическое давление определяют различными способами. Если при этом учитывают атмосферное давление, действующее на свободную поверхность жидкости, его называют абсолютным. Если отсчет ведется от относительного 0, за который принимается атмосферное давление, то говорят об избыточном или манометрическом давлении. Манометрическое давление есть разность между абсолютным давлением в жидкости и атмосферным давлением: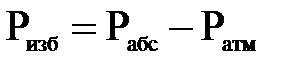

Встречаются случаи, когда гидростатическое давление в жидкости оказывается меньше атмосферного. В таких случаях говорить о вакууме (разрежении). Вакуум определяется разностью между атмосферным и абсолютным давлением в жидкости

( ).

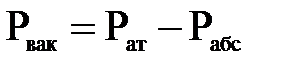Гидростатическое давление обладает двумя основными свойствами:

1. Оно направлено по внутренней нормали к площадке, на которую действует;

2. Его значение в данной точке не зависят от ориентировки в пространстве площадки, включающей эту точку.

Первое свойство является простым следствием того положения, что в покоящейся жидкости отсутствуют касательные и растягивающие напряжения. Предположим, что гидростатическое давление направлено не по нормали, т.е. не перпендикулярно, а под некоторым углом к площадке. Тогда его можно разложить на нормальную и касательную составляющие. Наличие последней ввиду отсутствия в покоящейся жидкости сил сопротивления сдвигающим усилиям неизбежно привело бы к движению вдоль площадки, т.е. нарушило бы ее равновесие. Следовательно, единственно возможным направлением гидростатического давления является его направление по нормами к площадке.

Предположим далее, что гидростатическое давление будет направлено по внешней, а не по внутренней нормали, т.е. не внутрь рассматриваемого объема, а наружу. Так как жидкость не оказывает сопротивления растягивающим усилием, то и в этом случае частицы жидкости придут в движение и ее равновесие будет нарушено. Значит, гидростатическое давление всегда направлено по внутренней нормали и представляет собой сжимающее давление.

Для доказательства второго свойства выделим в покоящейся жидкости призму сечением ΔF. Один торец призмы пусть будет перпендикулярен к образующей, а второй наклонен к ней под некоторым углом a. Длину призмы обозначим L, мысленно отбросив жидкость, окружающую выделенную в ней призму, заменим действие отброшенной жидкости силами давления на грани призмы. В соответствии со сказанным выше, это будут силы, нормальные к граням.

Обозначим далее через P0 и P1 средние давления соответственно на торце, перпендикулярном к образующей, и на скошенном торце, составим выражение для суммы проекции всех сил, действующих на призму и на ось, совпадающую с осью призмы.

Поскольку призма находится в равновесии, указанная сумма проекций сил должна равняться нулю. Пусть Q- проекция на эту ось единичной объемной силы, т.е. силы, приложенной к единице объема (в частном случае, когда из объемных сил действует только силы тяжести 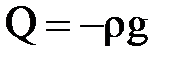). Тогда проекция объемных сил, приложенных к призме, будет QΔFL, проекция силы давления на торец А – Р₀ ΔF, а силы давления на скошенный торец –Р₁ (ΔF/sina) sina=-Р1ΔF.

Силы давления на боковые грани призмы проекций на ее ось не дадут. Поэтому сумма проекций всех сил составит ,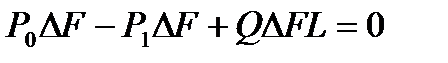

откуда .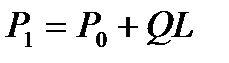

Следовательно, величина 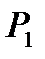оказывается не зависящей от угла a. В пределе (при ΔF, стремиться к нулю) 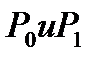представляют собой истинные значение давления в точках А и В и в соответствии с уравнением определяются положением точек в пространстве.

Таким образом, гидростатическое давление во всякой точке имеет одно и тоже значение по всем направлением и является функцией только ее координат: p=f(х,у,z).

Если давление например в точке А, изменится на величину 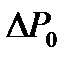, то на такую же величину изменится оно и в любой точке жидкости.