Диаграммы Коула—Коула

Большое значение при исследовании распределения времен релаксации имеют диаграммы, предложенные братьями Коул, так называемые диаграммы Коула—Коула. На диаграммах, Коула—Коула строится зависимость ε" от ε'.

В случае одного времени релаксации эта диаграмма представляет собой полуокружность, радиус которой 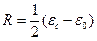и центр лежит на оси ε' на расстоянии 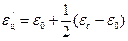от начала координат (Рис. 7‑9). Исследуя уравнения , видим, что при ωτ = 0 составляющие комплексной диэлектрической проницаемости ε' == ε_c и ε" == 0, и определяем соответствующую точку на окружности, лежащую на оси ε'. При 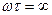эти составляющие ε' == ε₀ и ε" == 0, что дает другую точку на оси ε'. При ωτ == 1 получаем

Рис. 7‑9. Диаграмма Коула— Коула для случая, когда имеется только одно время релаксации

,

.

Уравнение окружности Коула—Коула можно записать в виде

.

Подставляя сюда значение ε' и ε" из уравнений и выбирая

,

,

Рис. 7‑10. Диаграмма Коула— Коула для случая, когда имеются два времени релаксации

можно показать, что уравнение удовлетворяется.

Если имеется несколько времен релаксации, то вид диаграмм Коула—Коула усложняется. Например, в случае двух времен релаксации на диаграмме будут две полуокружности вместо одной. Диаграмма Коула—Коула для частотной зависимости ε' и tgδ, изображенной на Рис. 7‑5, приведена на Рис. 7‑10.

Рассмотрим, как преобразуются диаграммы Коула—Коула в случае набора времен релаксации, группирующихся вокруг наиболее вероятного времени релаксации τ_в. Заметим, что выражение для комплексной диэлектрической проницаемости е* можно записать в двух эквивалентных формах:

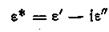
где ε' и ε" определяются уравнениями и

.

Отделяя в выражении вещественную часть от мнимой, можно показать, что оно сводится к уравнению .

Влияние распределения времен релаксации сказывается в том, что зависимость е* от ω становится меньше; это можно учесть, заменив выражение следующим:

,

где 0 < α < 1. Как вытекает из уравнения , диэлектрическая проницаемость при частоте ω == 0 равна ε_с и при ω = ¥ равна ε₀, а мнимая часть диэлектрической проницаемости пропадает.

Разделяя в вещественную и мнимую части, находим

где

,

.

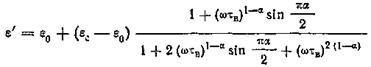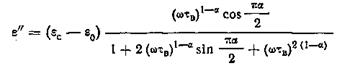При α = 0, что имеет место, когда есть только одно время релаксации, выражения и упрощаются и переходят в .

Как легко проверить, анализируя формулы и , максимальное значение ε' равно ε_с при ω = 0, минимальное значение ε' равно ε₀ при ω = ¥. Дифференцируя ε" по ωτ_в и приравнивая производную нулю, находим, что ε" проходит через максимум при ωτ_в = 1, достигая в максимуме величины

.

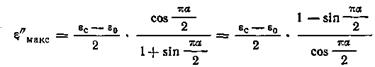Очевидно, это значение меньше, чем 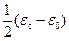—максимальная величина ε" при одном времени релаксации. Чем ближе α к единице, тем более размыта функция распределения времен релаксации и тем ниже величина ε" в максимуме. На плоскости ε'ε" диаграмма Коула—Коула в случае 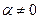представится дугой окружности, пересекающей ось ε' в точках ε₀ и ε_c, с радиусом

,

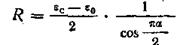и центром, лежащим ниже оси ε' на величину

.

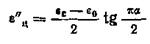Вдоль оси ε' расстояние от начала координат до центра окружности равно

Рис. 7‑11. Диаграмма Коула—Коула для случая, когда имеется набор времен релаксации

.

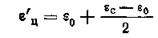Диаграмма Коула — Коула для случая 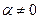представлена на Рис. 7‑11. Радиус, проведенный от центра окружности О в точки ε₀ и ε_c, составляет с осью ε' углы .

Имея результаты изменений ε' и ε" при различных частотах, диаграмму Коула — Коула строят следующим образом. Значение ε' и ε" при какой-либо частоте наносят на плоскость ε'ε" в виде точки. Затем наносят точку, координаты которой равны соответствующим значениям ε' и е" при другой частоте, и т. д. По экспериментальным точкам проводится кривая, которая, как показывает опыт, является либо дугой окружности, либо наложением нескольких дуг. Построив окружности, определяют угол и параметр распределения α. Если получается несколько дуг (см. Рис. 7‑10), значит в диэлектрике действует несколько механизмов релаксации или есть несколько видов молекул с различными временами релаксации.