Функция Гаврильяка—Негами.

Рис. 7‑17. Функция ε" = f(ε'), рассчитанная на ЭВМ по формуле Гаврильяка—Негами . Для данного модельного расчета взяты следующие значения: ε0 =8,6; ε¥ =2,7; 1 - λ = 0,91; 2pτ0 = 2,8×10-3 и β = 0,45; а частота внешнего электрического поля изменяется в пределах 30—107 Гц

Два различных эмпирических выражения функции распределения времен релаксации, использованных выше для описания «дугового сегмента» (2.4.1) и «скошенной дуги» могут быть обобщены в форме распределения Гаврильяка—Негами:

.

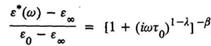Если в уравнении допустить, что β = 1, получим выражение функции распределения Коула—Коула (2.4.1). При λ = 0 получается выражение функции распределения Дэвидсона— Коула , а при одновременном равенстве λ == 0 и β = 1 формула представляет собой функцию Дебая. На Рис. 7‑17 представлена асимметричная дуговая функция ε" = f(ε'), соответствующая функции распределения Гаврильяка—Негами. Как видно из рисунка, эта теоретическая кривая линейна в области высоких частот и представляет собой дуговой сегмент в области низких частот.

Для количественного описания экспериментальных данных диэлектрических измерений эмпирической функцией распределения Гаврильяка—Негами необходимо графически определить значения пяти дисперсионных параметров (ε₀, ε_¥, λ, β, τ₀).

Параметр ε₀ получается экстраполяцией до пересечения с осью диэлектрической проницаемости ε' (с осью абсцисс), а параметр е_¥ находится линейной экстраполяцией экспериментальных точек до пересечения с той же осью в области высоких частот. Другие параметры ищутся численным расчетом.