Векторные диаграммы

Векторные диаграммы напряжений и сопротивлений последовательного колебательного контура выглядят следующим образом (рис. 3.1.6):

Рис. 3.1.6. Векторные диаграммы последовательного колебательного контура

При построении векторной диаграммы напряжений за исходный вектор принят вектор тока I, т. к. значение тока в последовательном колебательном контуре одинаково для всех элементов цепи.

Вектор напряжения на активном сопротивлении U_R совпадает по фазе с вектором тока I. Вектор напряжения на конденсаторе отстает от вектора тока на 90º. Вектор напряжения на катушке индуктивности опережает вектор тока на 90º. Суммарное напряжение U на зажимах всей цепи равно геометрической сумме трех указанных напряжений.

При построении диаграммы сопротивлений следует учесть, что во всей цепи протекает один и тот же ток I.

Сопротивление каждого элемента цепи можно получить, разделив соответствующий вектор напряжения на величину тока I. Поэтому диаграмма сопротивлений отличается от диаграммы напряжений только величиной масштаба.

Общее сопротивление последовательного колебательного контура равно геометрической сумме сопротивлений входящих в него элементов:

Отсюда видно, что сопротивление Z колебательного контура зависит от частоты w подводимого к нему напряжения.

Угол сдвига фаз между напряжением U и током I :

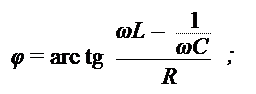Ток в контуре

Ток I в контуре определяется по следующей формуле:

I = ;

Ток в контуре будет наибольшим в том случае, когда величина сопротивления Z, зависящая от частоты w, будет минимальной:

Z = ;

Общее сопротивление Z будет минимальным при такой частоте w₀, при которой индуктивное сопротивление катушки окажется равным емкостному сопротивлению конденсатора:

Тогда Z = = R;

Следовательно, колебательный контур ведет себя так же, как активное сопротивление. В этом случае Z = R и j = 0º.

Условие, при котором соблюдается это равенство, называется резонансом.

Учитывая, что при резонансе можно найти значение резонансной частоты w ₀:

= 1;

w ₀ = ;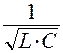

Величина r = w ₀ L = 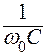называется характеристическим сопротивлением контура.

Характеристическое сопротивление представляет собой величину сопротивления каждого из реактивных элементов контура при резонансе. В этом случае значения сопротивлений указанных элементов равны по величине и противоположны по знаку.

Выразив значение резонансной частоты через параметры реактивных элементов, получаем:

r = w ₀ 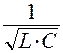L = · L = ;

Коэффициент Q = = = 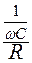называется добротностью контура.

Резонансная кривая

Практический интерес представляет отношение амплитуды тока в контуре при произвольной частоте к амплитуде тока при резонансной частоте w₀ :

Ток в контуре при любой частоте:

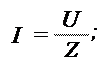Ток в контуре при резонансе:

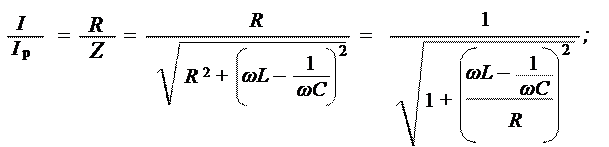Отношение тока при произвольной частоте к току при резонансе:

Это уравнение называется уравнением резонансной кривой колебательного контура.

Резонансная кривая полностью определяет свойства колебательного контура (рис. 3.1.7).

Рис. 3.1.7. Резонансная кривая колебательного контура