Теория свободного пробега.

Итак, рассмотрим основные положения "теории свободного пробега". Большая часть приводимых ниже результатов была получена Ванье. Как и ранее будем считать, что за время свободного пробега τ ион получает ускорение еЕ/т и за каждое столкновение теряет только часть своего импульса, так что

.

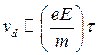Константа пропорциональности в написанном выражении должна зависеть от отношения масс т/М, партнеров по столкновению и от силы взаимодействия между, ионами и нейтральными частицами. Зависимость импульса, теряемого ионами за соударение, от масс частиц находим непосредственно из уравнений сохранения импульса и энергии. Если усредним затем полученное соотношение по всем столкновениям и пренебрежем незначительной разницей между средним от произведения и произведением средних, то в итоге получим

,

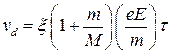где множитель ξ порядка единицы и может довольно сложным образом зависеть от силы взаимодействия между ионом и нейтральной частицей газа. Из-за приближенного характера усреднения скоростей по всем столкновениям этот множитель может еще слабо зависеть от масс частиц. Среднее время свободного пробега связано с сечением столкновения частиц σ и средней скоростью относительного движения 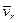ионов и молекул соотношением

.

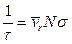В качестве 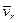разумно использовать среднеквадратичную скорость относительного движения

,

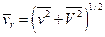здесь 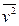определяет средний квадрат скорости ионов,
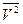— средний квадрат скорости молекул.

Любую погрешность, связанную с этим соотношением, в конце концов, можно включить в параметр ξ. В результате находим

.

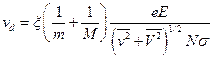Единственное, что нам осталось сделать, это найти 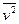, которая определяется как компонентой беспорядочного теплового движения, так и компонентой, связанной с движением ионов вдоль электрического поля.

В случае слабого поля величина 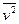целиком определяется влиянием «тепловой» компоненты движения, и из закона равнораспределения энергии по различным степеням свободы получаем уравнение

,

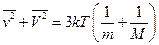из которого следует, что

.

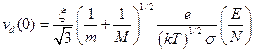Здесь мы получаем явную зависимость результата от параметра Е/N. Разделив последнее соотношение на Е, чтобы получить K(0), и используя соотношение Эйнштейна, чтобы получить коэффициент D, мы придем к явной зависимости коэффициента диффузии от плотности числа частиц газа вида 1/N. В дальнейшем мы увидим, что сравнение выражения для D с точным результатом в первом приближении теории Чемпена — Энскога показывает, что все размерные множители в уравнении выбраны правильно и что численное значение

.

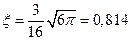Таким образом, в рассмотренном предельном случае множитель ξ случайно оказался не зависящим как от масс частиц, так и от закона их взаимодействия, и даже точность его достаточно высока, поскольку число 0,814 мало отличается от единицы.

В случае сильного внешнего поля вкладом в 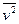от тепловой компоненты движения можно пренебречь, однако было бы неверным положить здесь просто 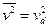. Дело в том, что столкновения приводят не только к потере ионами части их энергии, но также и к хаотизации энергии, так что полная средняя энергия ионов состоит частью из энергии дрейфового движения, к которой добавляется «случайная» составляющая энергии, также обусловленная влиянием поля[15]. Используя законы сохранения момента и энергии и усредняя их, как это делалось ранее, по всем столкновениям, получаем в итоге

.

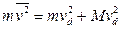Здесь последнее слагаемое обусловлено вкладом случайной компоненты энергии ионов. Таким образом, движение легких ионов в газе тяжелых молекул (m << M) происходит таким образом, что большая часть их энергии в поле обусловлена случайным движением, так как тяжелые молекулы газа весьма эффективно отклоняют налетающие ионы и отбирают лишь малую часть их энергии. Напротив, при движении тяжелых ионов в газе легких молекул (т >> М) большая доля их энергии связана с дрейфовым движением, поскольку легкие частицы неэффективны как в отклонении ионов, так и в отборе у них энергии движения. В случае равенства масс (т = М) средняя энергия ионов делится пополам между компонентами дрейфового и случайного движений. Подставляя выражение в уравнение и помня, что при сильных полях 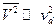, приходим к соотношению

.

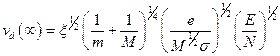Полученная зависимость очень хорошо описывает дрейф ионов в сильных полях, хотя в условиях, когда сечение столкновения, σ сильно зависит от 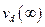, использовать ее сложно.

Представляет интерес проследите за полученной выше разной зависимостью скорости дрейфа v_d от напряженности поля в условиях слабого и сильного полей:

,

.

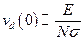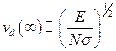Так, если σ не зависит от параметра Е/N, то v_d изменяется пропорционально первой степени Е/N при слабом поле и пропорционально корню квадратному из Е/N — при сильном. За исключением случая твердых сфер, сечение рассеяния σ, однако, зависит от относительной скорости столкновения v_r. Таким образом, в пределе слабого внешнего поля σ зависит от температуры газа, поскольку скорость v_r обусловлена тепловым движением, и соотношение оказывается точным. При сильных полях вклад теплового движения в полную энергию ионов можно считать малым, и σ становится функцией скорости дрейфа v_d, а, значит, и параметра Е/N. Как видим, предположение о зависимости v_d от Е/N в степени ¹/₂ для сильного поля оказывается только приближенным, но утверждение о независимости 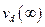от температуры газа должно выполняться точно. Экспериментальные данные, полученные при анализе движения ионов инертного газа в среде родственных молекул при сильных полях, подтверждают, что скорость дрейфа следует зависимости (Е/N)^1/2. В любом случае можно утверждать, что динамические характеристики ионов в газе зависят от напряженности поля только в комбинации Е/N.

В условиях, когда наложенное поле является промежуточным между предельными значениями слабого и сильного полей, вклады в полную энергию ионов от теплового движения и от поля оказываются сравнимыми, так что, комбинируя и , получаем

.

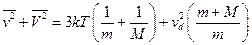Подставив последнее выражение в формулу , найдем в итоге соотношение для скорости дрейфа ионов

,

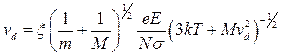которое сводится к квадратному уравнению относительно :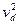

.

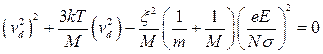Его решение позволяет получить разумную интерполяционную формулу для скорости v_d при любых напряженностях поля, однако, прежде чем искать точное решение, можно указать ряд важных особенностей решения.

Во-первых, скорость v_d зависит от Е и N только через отношение Е/М, что отмечалось нами и ранее. В действительности, v_d представляет собой функцию параметра еЕ/Nσ.

Во-вторых, в случае умеренно слабого внешнего поля можно разложить правую часть уравнения в ряд по степеням малой величины 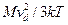и путем последовательных приближений найти вид функции v_d. Легко показать, что дрейфовая скорость v_d определяется только целыми степенями параметра (Е/N)², что было получено нами из общих соображений ранее [см. ]. В частности, будем иметь приближенно

,

.

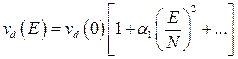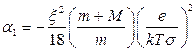Наконец, в-третьих, в случае умеренно сильного электрического поля можно разложить правую часть уравнения в ряд по степеням малой величины 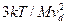и получить в итоге

,

.

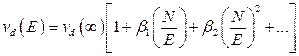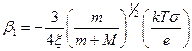Отметим здесь, что написанное разложение по обратным степеням параметра Е/N содержит члены со всеми целыми показателями, тогда как в случае достаточно слабого поля ряд включал только члены с четными степенями Е/N.

Аналогичным образом можно получить также некоторые приближенные результаты для коэффициента диффузии D. Используя представления о свободном пролете частиц между столкновениями (или средней длине свободного пробега частиц), приходим к хорошо известному выражению для D

;

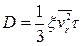здесь множитель ξ включен нами для того, чтобы удовлетворялось соотношение Эйнштейна. При выводе последнего выражения подразумевалась изотропия пространственного распределения частиц газа, так что данный результат неприменим к случаю сильного внешнего поля. Можно, однако, разумным образом расширить область применимости данных представлений на поле любой напряженности, если описывать диффузию ионов как изотропный случайный процесс, наложенный на упорядоченное движение вдоль поля со скоростью дрейфа v_d. Тогда придется ввести коэффициенты поперечной и продольной диффузии частиц, равные

,

,

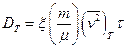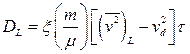причем появление множителя т/μ обусловлено тем, что мы сделали переход от относительной скорости столкновения частиц к средней скорости движения ионов. Только при движении ионов вдоль электрического поля следует выделять в их полной средней энергии энергию дрейфового движения.

Поскольку в формулах , мы имеем дело только с компонентами скорости ионов вдоль и поперек поля, численный множитель ¹/₃ должен быть нами опущен. Появление его в формуле связано прежде всего с тем, что было использовано равенство

.

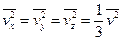Дальнейшая детализация расчета может ответить на вопрос, каким образом энергия делится между компонентами движения вдоль и поперек поля. Ответ на этот вопрос можно найти в специальной литературе. Мы же ограничимся в заключение несколько замечаниями общего характера о теории свободного пробега.

Хотя и очевидно, что нам удалось получить ряд вполне разумных результатов, затратив минимум усилий на вычисления, все же достигнутый успех следует прокомментировать двумя критическими замечаниями.

Во-первых, такой вывод до некоторой степени случаен.

Во-вторых, как отметил в свое время Крамерс, «...выводы, которые мы при этом делаем, вполне могут оказаться беспочвенными размышлениями, чему кинетическая теория газов знает немало примеров».

Упоминание о случайности связано с тем, что теория диффузии, использующая понятие средней длины свободного пробега частиц, приводит к хорошим результатам только в том случае, когда пробные частицы (ионы) в газе присутствуют в качестве малой добавки. Если же эту теорию мы применим к анализу произвольной смеси двух газов, то непосредственно получим сильную зависимость коэффициента диффузии от относительного состава газов, что противоречит как результатам эксперимента, так и более строгой теории.

Попытки улучшить теорию, основанную на понятии средней длины свободного пробега, путем введения поправок на сохраняемость скоростей частиц после соударения сразу же приводят к «непреодолимым» трудностям, поскольку расчеты сильно усложняются и сходимость приближений оказывается слабой. Практически все более точные результаты были получены путем отказа от элементарной теории свободного пробега частиц, когда отыскивалось решение кинетического уравнения Больцмана, или подобного ему интегро-дифференциального уравнения. Лишь недавно была установлена математически строгая связь между теорией диффузии, использующей понятие средней длины свободного пробега частиц, и теорией Чепмена—Энскога решения кинетического уравнения. Что касается подвижности ионов, то подобная связь может быть установлена только для случая исчезающе малого электрического поля.