Диффузия в стёклах и стеклообразующих расплавах

Диффузия – это процесс самопроизвольного выравнивания концентрации компонентов за счёт перемещения отдельных ионов и атомов под действием градиента химического потенциала grad μ_i.

grad μ_i – движущая сила диффузии.

Диффузионный поток в общем случае рассчитывается по уравнению:

.

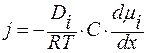Для простых случаев это уравнение преобразуется с учётом градиента концентраций диффундирующих компонентов:

.

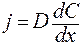Возможность перемещения частиц через диффузионные процессы проявляется в связи с их тепловым движением. Колебания атомов или ионов около положений равновесия дают возможность перескока в соседнее положение равновесия, если оно оказывается вакантным. Диффузионный поток реализует стремление системы к минимальной энергии Гиббса.

В том случае, если диффузия частицы протекает в структуре, представленной подобными же частицами, говорят о самодиффузии (например, диффузия катиона натрия в стекле Na₂O-SiO₂). Если природа частиц различна, то выравнивание концентраций протекает за счёт гетеродиффузии (диффузия катиона калия в стекле Na₂O-SiO₂).

Особенности диффузии в силикатных стёклах:

1. Кремний и кислород прочно связаны в кремнекислородном каркасе. Поэтому диффузия катионов-стеклообразователей протекает значительно медленнее, чем катионов–модификаторов:

D_Si4+<<D_Na+

2. Так как анионов кислорода в стекле много и они являются общими для всех катионов, то достаточно незначительного перемещения кислорода чтобы компенсировать изменение заряда при диффузии катионов.

D_МеО ≈ D_Ме²⁺ , так как ионов О^2- много.

3. Механизм диффузии в стёклах во многом аналогичен диффузионному перемещению в кристаллах, так как в обоих случаях перемещаются, в основном, катионы небольших размеров.

Известно, что в кристаллах частицы диффундируют, как правило, по двум вариантам: по вакансиям решетки и по междуузлиям. В стёклах реализуются оба варианта, но обычно ионы–модификаторы диффундируют по межтетраэдрическим полостям, т.к. энергия активации диффузии в этом случае наименьшая.

Энергия активации диффузии для стёкол и кристаллов отличаются незначительно. Так для системы Na₂O∙2CaO∙3SiO₂ энергия активации диффузии катионов натрия составляет для стеклообразного состояния Е_диф= 125 кДж/моль, для кристаллического состояния – Е_диф = 125 кДж/моль. Коэффициенты диффузии при температуре 800^оС соответственно равны: D_ст = 5,3∙10^-9 см²/с и D_кр = 6,8 ∙10^-10 см²/с.

Так как диффузия протекает по междуузлиям, то энергия активации диффузии в гораздо меньшей степени зависит от природы диффундирующего катиона, чем от структуры стекла.

Температурная зависимость коэффициента диффузии в кристаллах описывается уравнениями:

;

.

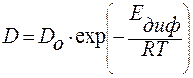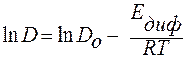Для стёкол необходимо учитывать две особенности:

1. Вблизи температуры стеклования меняется структура стекла, поэтому уравнение можно использовать за пределами области размягчения.

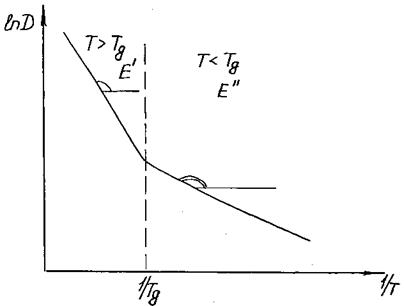
2. При замораживании структуры расплава в стекле образуются межтетраэдрические полости, по которым могут диффундировать катионы-модификаторы. Поэтому энергия активации диффузии при низких температурах будет меньше, чем в расплаве. В расплаве ионы упакованы более плотно, чем в твердом стекле. При высоких температурах Т > T_g структура стеклорасплава ближе к равновесной (рис. 4.3).

Рис. 4.3. Температурная зависимость коэффициентов диффузии компонентов в стекле

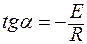; E΄ > E΄΄.

Если предположить, что диффундирующий ион – это сферическая частица, то коэффициент диффузии можно рассчитать по уравнению Стокса–Эйнштейна:

,

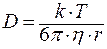где k – постоянная Больцмана;

η – вязкость расплава;

r – радиус диффундирующей частицы.

Коэффициент диффузии связан с электропроводностью уравнением Нернста-Эйнштейна:

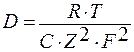.κ,

C – концентрация ионов;

Z – заряд иона;

F – число Фарадея;

Κ – электропроводность.

Экспериментальные методы определения коэффициента диффузии в стёклах такие же, как для кристаллов и высокотемпературных расплавов. В частности, используются метод анализа изменения концентрации диффундирующих изотопов, метод вращающегося диска и другие.