Уравнение диффузии. Второй закон Фика.

Рассмотрим теперь ансамбль ионов, диффундирующих через неограниченную среду газа, в которой нет ни источников, ни стоков частиц. Из определения плотности потока частиц 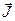следует, что полное число частиц, которые в единицу времени покидают некоторый объем газа через охватывающую его произвольную замкнутую поверхность, дается интегралом 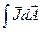. По теореме Гаусса можно преобразовать поверхностный интеграл в объемный и выразить число покидающих данный объем частиц через интеграл 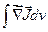, где интегрирование ведется по объему, ограниченному поверхностью A. Если обозначить плотность числа ионов через п, то, согласно сказанному выше, имеет место равенство

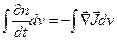
или

.

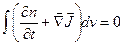Поскольку выбор поверхности А был произволен, подынтегральное выражение должно обращаться в нуль. Таким образом, получаем уравнение

,

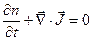которое называется уравнением непрерывности.

Согласно закону диффузии Фика , 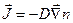, имеем

,

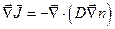и уравнение непрерывности дает соотношение

,

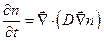которое известно как нестационарное уравнение диффузии, или второй закон Фика. Отметим, что в уравнении учитывается возможная зависимость коэффициента диффузии D от координаты (через зависимость его от плотности числа частиц).

Теперь мы можем проверить вид функции распределения ионов, даваемый выражениями и . Подставляяих непосредственно в уравнение , мы видим, что обе функции распределения удовлетворяют уравнению диффузии.

Предположим далее, что внутри наполненного газом сосуда установилось некоторое равновесное распределение ионов n₀(х, у, z). Чтобы поддерживать это установившееся распределение, мы должны непрерывно вводить в газ новые ионы для восполнения потерь заряженных частиц в результате ухода их на стенки сосуда при диффузии. Можно создавать новые ионы путем непрерывной ионизации газа рентгеновским или СВЧ излучением. Представим себе теперь, что в момент времени t = 0 источник ионизации газа мгновенно выключается. Если предположить, что D не зависит от координаты, и разделить переменные в уравнении , записав

,

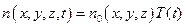то для функции T(t) получим уравнение, решение которого имеет вид

,

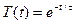где τ — постоянная времени затухания[13].

Таким образом, уравнение приводит к не зависящему от времени уравнению диффузии

.

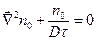Решение уравнения для n₀(х, у, г) представляет собой задачу на собственные значения; характер решения зависит от геометрии сосуда и соответствующих граничных условий.

Граничные условия

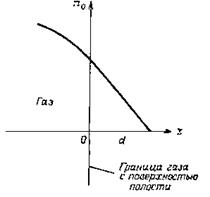Рис. 2‑1. Линейная экстраполяция плотности числа ионов n, за пределы физической границы полости для нахождения длины экстраполяции d. Постановка граничных условий основывается на предположении, что ионы не отражаются от стенки полости, а либо нейтрализуются на проводящей поверхности, либо прилипают к поверхности диэлектрика.

Поскольку уравнение диффузии является дифференциальным уравнением второго порядка, его общее решение должно содержать две произвольные постоянные интегрирования.При решении какой-либо частной задачи значения этих постоянных определяют из граничных условий и некоторых дополнительных физических предпосылок.

При исследовании диффузии ионов в газе, заключенном в некоторый сосуд, обычно предполагают, что плотность числа ионов всюду конечна, а на стенках сосуда исчезающе мала. Если это условие понимать как обязательное обращение в нуль плотности потока ионов внутрь объема газа на стенках сосуда, с тем чтобы никакие ионы не отражались в объем газа после соударения со стенкой, то тогда по теории диффузии обычно требуется такое изменение плотности числа ионов вблизи стенки, чтобы линейная экстраполяция плотности за пределы стенки обращала ее в нуль на конечном расстоянии d за внутренней поверхностью сосуда (Рис. 2‑1). Довольно длинные вычисления показывают, что в случае плоской границы

,

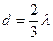где λ — средняя длина свободного пробега ионов относительно их упругих столкновений с молекулами газа.

Расстояние d обычно называют длиной линейной экстраполяции; оно служит мерой эффективного увеличения размеров сосуда, которое требуется для математического описания процесса диффузии в замкнутом объеме. Для сосудов различных геометрических форм значения длины d слегка отличаются друг от друга.

Анализ диффузии ионов и электронов в газе показывает, что длина линейной экстраполяции пренебрежимо мала по сравнению с размерами сосуда, и при расчетах ею пренебрегают. Другими словами, граничные условия формулируют таким образом, что плотность числа электронов и ионов на внутренней поверхности сосуда обращается в нуль. Однако в задаче о диффузии нейтронов длина d часто имеет значительную величину и должна учитываться теорией.