Расплывание облака ионов вследствие диффузии через неограниченный объем газа
В данном параграфе и ряде последующих мы ограничимся рассмотрением вопросов расплывания облака ионов в пространстве вследствие диффузии их в газе при тепловых энергиях и низкой степени ионизации, когда ионы взаимодействуют только с молекулами газа, а не с другими ионами и электронами. Предположим также, что ионы не вступают в химические реакции с нейтральными частицами газа. Полученные ниже результаты окажутся полезными при анализе различных практических вопросов и некоторых типов экспериментов, обсуждаемых в наших лекциях.
Прежде всего, рассмотрим поведение некоторого числа ионов N, помещенных в начале одномерной системы координат. Представим себе, что ионы в момент времени t = 0 начинают диффундировать через свободный от внешних полей газ, однородно заполняющий все пространство и находящийся при постоянном давлении. Через интервал времени t на расстоянии х от начала координат плотность числа ионов окажется равной
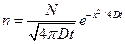 ,
,
где D — коэффициент диффузии ионов через газ[11].
Это уравнение, так же называют соотношением Эйнштейна. Для любого момента времени кривая зависимости n от расстояния х имеет вид гауссовой функции ошибок. С течением времени форма кривой становится все более плоской.
С помощью функции распределения ионов можно рассчитать среднее и среднеквадратичное смещения ионов из начала координат:
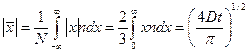
и
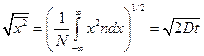 .
.
В случае трехмерного начального распределения ионов значение их плотности на расстоянии r в момент времени t будет равно
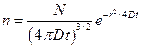 .
.
Среднее и среднеквадратичное смещение ионов в этом случае равны
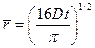
и
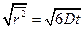 .
.
При рассмотрении двумерной задачи имеем
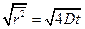 .
.
Написанные выше соотношения могут оказаться полезными при оценке среднего времени жизни ионов т относительно столкновений со стенками сосуда, содержащего газ. Из выражений для среднего смещения ионов найдем, что
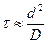 ,
,
где d определяет соответствующий размер сосуда с газом.
Можно провести и более строгое вычисление времени t для различной геометрии сосудов[12]. Соответствующие результаты записываются следующим образом:
а) для бесконечно длинной трубки прямоугольного сечения со сторонами a и b
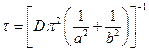 ;
;
б) для бесконечно длинного цилиндра радиусом r0
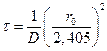 ;
;
в) для сферы радиусом r0
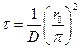 .
.
Для иллюстрации того, как пользоваться приведенными выше результатами решим задачу.
Задача.
Рассчитать время жизни иона, который первоначально находился на оси цилиндрической трубки радиусом 1 см, содержащей азот при давлении 1 мм рт. ст. и комнатной температуре.
Решение. Применим соотношение . Беря значение коэффициента диффузии равным 50 см2/с, найдем, что время τ составляет около 3×10-3 с. За это время ион переместится на расстояние 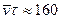 см, где
см, где 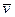 — средняя скорость теплового движения.
— средняя скорость теплового движения.
Дата добавления: 2020-02-05; просмотров: 685;











