Алгоритм расчета однофакторного дисперсионного анализа

Проведение ДА связано с большими вычислениями, поэтому желательно применение вычислительной техники и упрощающих приемов. Так, перед началом «ручного» счета все исходные данные можно уменьшить (увеличить) на одну и ту же величину – на дисперсиях это не отразится.

Оформив все данные в виде таблицы 4.1 и, используя зависимости (4.6) – (4.18), алгоритм однофакторного ДА можно представить в виде следующей последовательности вычислений

1 Подсчитывают итоги по столбцам – суммы наблюдений по каждому уровню фактора Х:

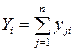. (4.26)

2 Вычисляют сумму квадратов всех наблюдений:

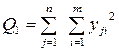. (4.27)

3 Вычисляют сумму квадратов итогов по столбцам, деленную на число наблюдений в столбце:

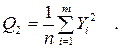(4.28)

4 Рассчитывают квадрат общего итога, деленный на число всех наблюдений (корректирующий член):

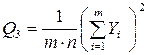. (4.29)

5 Определяют сумму квадратов для столбца:

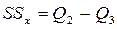. (2.30)

6 Определяют общую сумму квадратов:

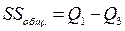. (4.31)

7 Определяют остаточную сумму квадратов для оценки ошибки эксперимента:

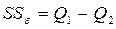. (4.32)

8 Рассчитывают оценку дисперсии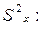

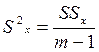. (4.33)

9 Рассчитывают оценку дисперсии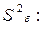

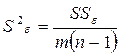. (4.34)

10 Оценивается влияние фактора Х по зависимости (4.18) - (4.25).

Результаты расчета, как правило, представляются в виде следующей таблицы дисперсионного анализа.

Таблица 4.2 – Однофакторный дисперсионный анализ с равным числом повторений опытов

Компоненты дисперсии	Число степеней свободы	Сумма квадратов	Средний квадрат (оценка дисперсии)	Математическое ожидание среднего квадрата
Междууровневая	m-1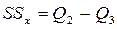
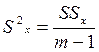
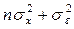
Внутриуровневая	m(n-1)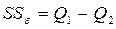
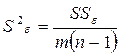
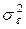
Общая (полная)	mn-1			–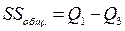

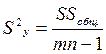
В случае, когда на различных уровнях фактора проводится разное число параллельных опытов, можно, ориентируясь на уровень с меньшим числом, отбросить лишние наблюдения в остальных уровнях. Однако такое отбрасывание нежелательно, так как существенно снизит точность проводимого анализа. Тем более что новая схема вычислений лишь не многим будет отличаться от случая равных столбцов. Пусть на уровне х_i проведено n_i параллельных наблюдений. Общее число всех наблюдений будет равно:

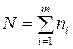. (4.35)

Определим:

1 Итоги по столбцам – суммы наблюдений по каждому уровню фактора х_i:

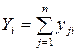. (4.36)

2 Суммы квадратов всех наблюдений:

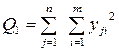. (4.37)

3 Сумму квадратов итогов по столбцам, деленных на число наблюдений в соответствующем столбце:

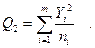(4.38)

4 Квадрат общего итога, деленный на число всех наблюдений:

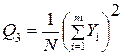. (4.39)

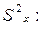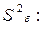Дальнейшие расчеты проводятся по формулам (4.30) - (4.34). Если оценки дисперсий и значимо отличаются друг от друга, то дисперсию фактора Х можно вычислить по формуле:

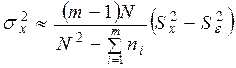. (4.40)

При этом соотношение для чисел степеней свободы следующее:

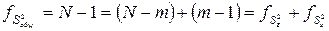. (4.41)

Задача 4.1.

Пороховой завод изготовил заряды к артиллерийским боеприпасам на четырех однотипных поточных линиях. С каждой поточной линии случайным образом было выбрано и отстрелено в одинаковых условиях по пять боеприпасов. Результаты замеров начальных скоростей полета снарядов V₀, м/с, для каждой группы приведены в таблице 4.3.

Таблица 4.3 – Результаты испытаний

Стоит задача: выяснить, существенно ли влияние данных поточных линий на величину начальной скорости полета снарядов V_0.

Решение.

1 Проверяем предпосылки ДА.

Пусть из априорных данных известно, что результаты наблюдений являются независимыми случайными величинами, имеющие нормальный закон распределения; опыты, проведенные нами, равноточны, а случайные ошибки наблюдений подчиняются нормальному закону. Однородность выборочных дисперсий проверим по критерию Кохрена.

– определяем средние по столбцам:

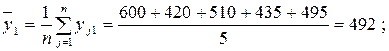
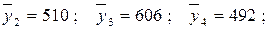
– определяем оценки дисперсий для каждого столбца:

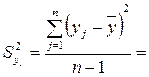
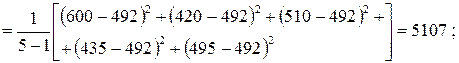
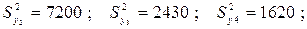
– определяем расчетное значение критерия Кохрена:

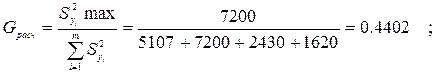
– определяем табличное значение G-критерия по таблице приложения 4:

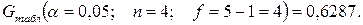
Так как G_расч<G_табл., то оценки дисперсий однородны и можно приступить к проведению ДА.

2 Подсчитываем итоги по столбцам:

,

;

;

;

.

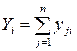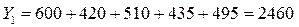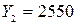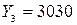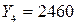3 Вычисляем сумму квадратов всех наблюдений:

;

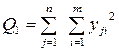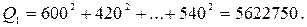
4 Вычисляем сумму квадратов итогов по столбцам, деленную на число наблюдений в столбце:

;

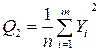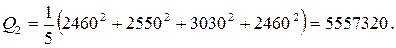
5 Рассчитаем квадрат общего итога, деленный на число всех наблюдений:

;

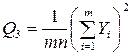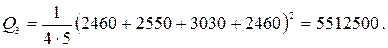
6 Определяем сумму квадратов для столбца:

;

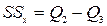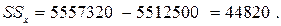
7 Определяем общую сумму квадратов:

;

.

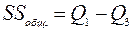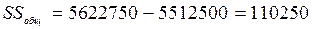8 Определяем остаточную сумму квадратов для оценки ошибки эксперимента:

;

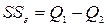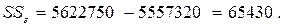
9 Рассчитывают оценку дисперсии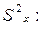

;

.

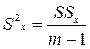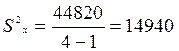10 Рассчитывают оценку дисперсии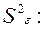

;

.

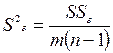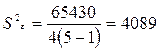11 Вычисляем расчетное значение F - критерия:

;

.

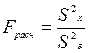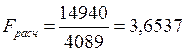12 Определяем критическое табличное значение F - критерия (приложение Б):

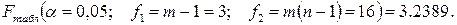
13 Сравним F_расч и F_табл:

.

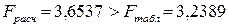Таким образом, влияние поточных линий на величину начальной скорости полета снаряда V₀ следует признать значимым.

14 Определяем величину влияния номера поточной линии:

.

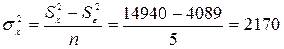15 Производим сравнение влияния номеров поточных линий по критерию Дункана. С этой целью:

- вычисляем нормированную ошибку среднего:

;

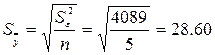- располагаем значения средних по столбцам (смотреть таблицу 2.3) в порядке возрастания их величин:

;

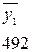
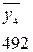
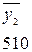
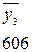- выписываем из таблицы Дункана (приложение В)

;

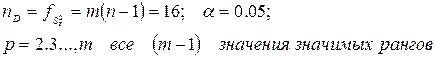
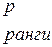
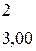
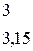
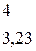- вычисляем (m-1) наименьшие значимые ранги (НЗР), умножая ранги на нормированную ошибку среднего:

;

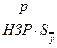
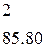
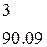
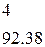- проверяем значимость различия между средними по столбцам для всех m(m-1)/2 парами:

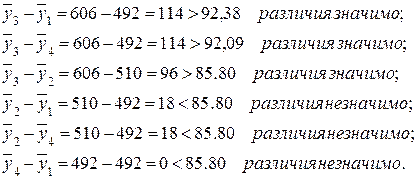
Таким образом, для выпуска однородной продукции усовершенствование целесообразно начать с третьей поточной линии.