Корней характеристического уравнения на комплексной плоскости

Пусть система описывается следующим дифференциальным уравнением в операторном виде

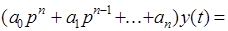
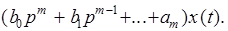(1)

Здесь 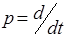- оператор дифференцирования, 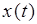- входное воздействие, 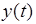- выходная величина.

Решение уравнения (1) представим в виде

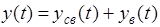, (2)

где 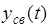- свободная составляющая решения, которая определяется решением однородного дифференциального уравнения (1) без правой части

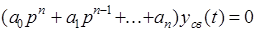, (3)

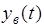- вынужденная составляющая решения, определяется как частное решение неоднородного дифференциального уравнения

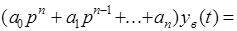
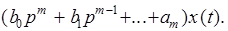(4)

В соответствии с определением устойчивости по А.М. Ляпунову, система, описываемая уравнением (1) будет асимптотически устойчивой, если при 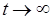свободная составляющая 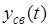, определяемая решением дифференциального уравнения (3), будет стремиться к .

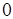Решение дифференциального уравнения (3) ищут в виде

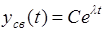. (5)

Продифференцировав это выражение раз, подставив результаты дифференцирования в (3) и сократив на общий множитель 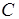, получим

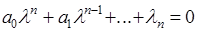. (6)

Данное алгебраическое уравнение носит название характеристического уравнения. Формально оно может быть получено из левой части уравнения системы (1) при входном воздействии

. (7)

Следует заметить, что в этом уравнении не является символом дифференцирования, так как 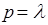. Таким образом (7) является характеристическим уравнением исследуемой системы, а его корни определяют характер переходных процессов в системе

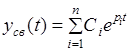. (8)

В этом решении 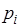- корни характеристического уравнения, 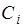- постоянные интегрирования, определяемые из начальных условий.

Полагая, что 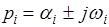и используя известную формулу Эйлера

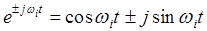, (9)

решение (8) может быть представлено в следующем виде

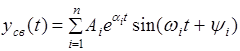, (10)

где 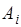и 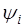- новые постоянные интегрирования. Из этого решения следует, что на устойчивость системы влияет знак вещественной части корней характеристического уравнения 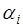. Если характеристическое уравнение имеет хотя бы один корень с вещественной частью 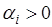, то при 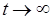переходной процесс будет расходящимся и только когда у всех корней 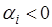, то при 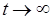переходный процесс будет затухающим. Наличие мнимой части в корне 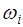говорит о присутствии составляющей в решении (10) колебательного характера. Если при этом 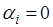, то при 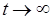в системе имеют место незатухающие колебания, ес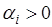ли или 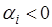, то в системе будут соответственно расходящиеся и затухающие колебания.

Необходимое и достаточное условие устойчивости формулируется следующим образом: для того чтобы линейная система была асимптотически устойчива, необходимо и достаточно, чтобы все корни ее характеристического уравнения имели отрицательные вещественные части, иначе располагались в левой полуплоскости корней.

Например для системы, имеющей характеристическое уравнение

,

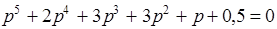корни на комплексной плоскости корней располагаются следующим образом

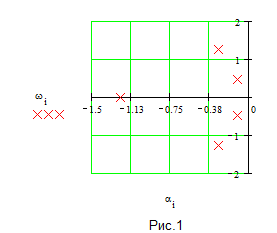
Здесь по оси ординат откладывается вещественная часть корня, а по оси абсцисс его мнимая часть. Как видно из Рис.1. все пять корней полинома расположены в левой полуплоскости, причем 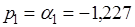- действительный корень, а

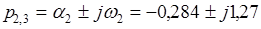
и

,

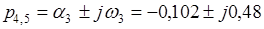комплексно-сопряженные корни. Таким образом рассматриваемая система устойчива.

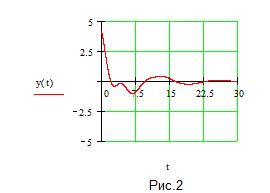
На Рис.2 изображен переходной процесс, полученный в Mathcad 7. Как следует из графика переходной процесс является затухающим.

Обычно корни с отрицательными вещественными частями называют левыми, а корни с положительными вещественными частями - правыми. Если система имеет хотя бы один правый корень, то она неустойчива. Если корень является мнимым, то есть расположен на мнимой оси плоскости корней, то система находится на границе устойчивости.