Запишем его передаточную и частотную функцию

,

.

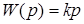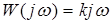Частотные и временная характеристика звена имеют вид

, ,

, , ,

.

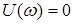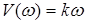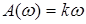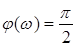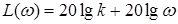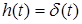На Рис.4.11. представлена ЛЧХ звена

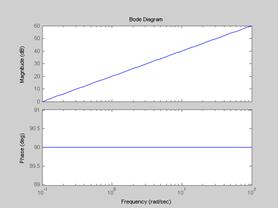
Рис.4.11.

В технике не существует реальных объектов, которые бы описывались таким уравнением. Оно соответствует идеальному дифференцирующему звену. В качестве примера такого звена можно назвать тахогенератор, входной величиной которого является угол поворота ротора, а выходной - напряжение на якоре.

Форсирующим звеном называется звено, которое описывается следующим уравнением

.

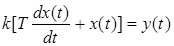Его передаточная функция имеет вид

.

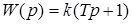ЛЧХ звена представлены на Рис.4.12.

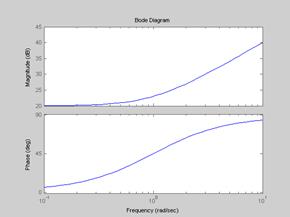
Рис.4.12.

С ростом частоты входного сигнала, у сигнала на его выходе растет амплитуда, причем после точки излома ( 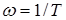) с интенсивностью 20 дБ/дек. Фаза растет от 0 до 90 градусов.

Форсирующее звено 2-го порядка имеет следующее дифференциальное уравнение

.

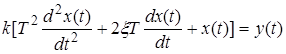Его передаточная функция

.

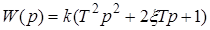На Рис.4.13 представлены ЛЧХ звена

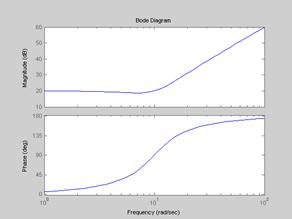
Рис.4.13.

С ростом частоты входного сигнала, у сигнала на его выходе растет амплитуда, причем после точки излома ( 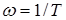) с интенсивностью 40 дБ/дек. Фаза растет от 0 до 180 градусов.