Исследование устойчивости САУ с помощью критерия Найквиста
Критерий Найквиста относится к частотным критериям устойчивости, был разработан американским ученым Г. Найквистом в 1932 году и позволяет судить об устойчивости замкнутой системы по виду АФЧХ разомкнутой системы.
Рассмотрим систему

Рис.1.
Здесь 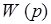 - передаточная функция разомкнутой системы. Тогда передаточная функция замкнутой системы имеет вид
- передаточная функция разомкнутой системы. Тогда передаточная функция замкнутой системы имеет вид
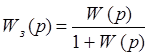 . (1)
. (1)
Приравняв знаменатель нулю, получим характеристическое уравнение замкнутой системы
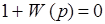 . (2) Обозначим
. (2) Обозначим
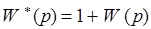 . (3)
. (3)
Представим передаточную функцию разомкнутой системы в виде отношения двух полиномов
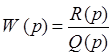 , (4)
, (4)
где 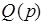 - характеристический полином степени
- характеристический полином степени 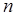 разомкнутой системы,
разомкнутой системы, 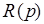 - полином степени
- полином степени 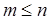 . Тогда
. Тогда
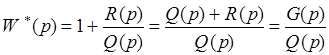 . (5)
. (5)
Заметим, что в этом выражении степени полиномов числителя и знаменателя одинаковы и равны 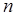 .
.
Пусть 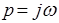 , тогда
, тогда
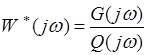 . (6)
. (6)
Предположим, что разомкнутая система неустойчива и ее характеристическое уравнение имеет 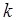 правых и
правых и 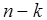 левых корней. Будем также предполагать, что замкнутая система неустойчива и имеет
левых корней. Будем также предполагать, что замкнутая система неустойчива и имеет 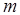 правых и
правых и 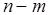 левых корней. Тогда на основании принципа аргумента можно утверждать, что при изменении частоты
левых корней. Тогда на основании принципа аргумента можно утверждать, что при изменении частоты 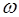 от
от 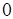 до
до 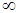 изменение аргумента
изменение аргумента 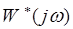 составит
составит
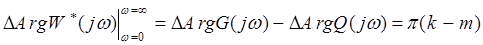 . (7)
. (7)
Для того, чтобы замкнутая система была устойчивой необходимо и достаточно, чтобы все корни ее характеристического уравнения были левыми, то есть 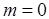 . В этом случае
. В этом случае
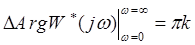 . (8)
. (8)
Так как в соответствии с выражением (3) функции 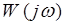 и
и 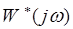 отличаются на единицу, то поворот вектора
отличаются на единицу, то поворот вектора 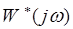 вокруг начала координат соответствует повороту вектора
вокруг начала координат соответствует повороту вектора 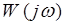 вокруг точки
вокруг точки 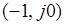 .
.
Дадим теперь следующую формулировку критерия устойчивости Найквиста. Для того, чтобы замкнутая система была устойчивой при неустойчивой разомкнутой системе необходимо и достаточно, чтобы АФЧХ разомкнутой системы 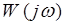 при изменении частоты
при изменении частоты 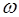 от
от 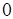 до
до 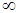 охватывала точку
охватывала точку 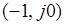 в положительном направлении (против часовой стрелки)
в положительном направлении (против часовой стрелки) 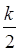 раз, где
раз, где 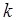 - число правых корней характеристического уравнения разомкнутой системы.
- число правых корней характеристического уравнения разомкнутой системы.
На Рис. 4.3 изображена АФЧХ устойчивой системы в замкнутом состоянии, которая в разомкнутом состоянии была неустойчива и имела два правых корня.
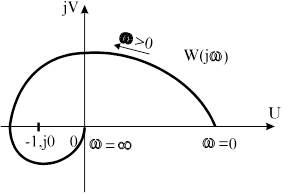
Рис. 4.2.
На практике обычно дается следующая формулировка критерия Найквиста. Если разомкнутая САУ устойчива, то замкнутая система будет устойчива , если АФЧХ разомкнутой системы  не охватывает точку с координатами
не охватывает точку с координатами  .
.
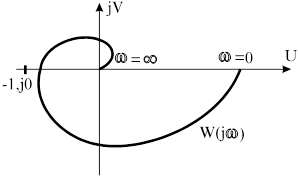
Рис. 4.3. АФЧХ устойчивой системы
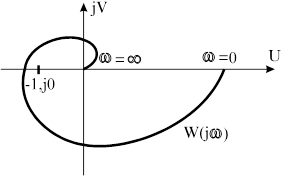
Рис. 4.4. АФЧХ неустойчивой системы
Если 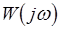 проходит через точку
проходит через точку 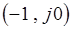 , то САУ находится на границе устойчивости .
, то САУ находится на границе устойчивости .
Рассмотренные выше АФЧХ относятся к статическим САУ . У астатических систем, содержащих интегрирующие звенья, АФЧХ при 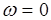 стремиться к бесконечности и , следовательно , не образует замкнутого контура. Для того, чтобы определить устойчивость астатической замкнутой САУ необходимо построить АФЧХ разомкнутой системы при
стремиться к бесконечности и , следовательно , не образует замкнутого контура. Для того, чтобы определить устойчивость астатической замкнутой САУ необходимо построить АФЧХ разомкнутой системы при 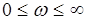 , дополнить ее дугой
, дополнить ее дугой 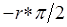 , (где
, (где 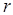 - порядок астатизма ) окружности бесконечно большого радиуса
- порядок астатизма ) окружности бесконечно большого радиуса 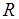 и затем применять критерий устойчивости Найквиста.
и затем применять критерий устойчивости Найквиста.
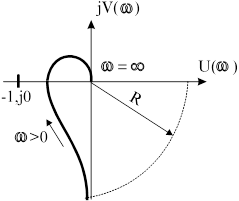
Рис. 4.5.
На Рис. 4.5 приведена АФЧХ разомкнутой устойчивой системы с астатизмом первого порядка. Замкнутая система в этом случае также устойчива . На Рис. 4.6 показана АФЧХ разомкнутой неустойчивой системы с астатизмом второго порядка . Для этого случая замкнутая система неустойчива, так как точка с координатами 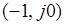 охватывается АФЧХ, дополненной дугой бесконечно большого радиуса в отрицательном направлении.
охватывается АФЧХ, дополненной дугой бесконечно большого радиуса в отрицательном направлении.
Рис.4.6.
На практике широкое применение получил критерий устойчивости Найквиста с применением вместо АФЧХ логарифмических амплитудно-частотных характеристик.
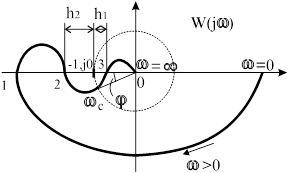
Рис. 4.7.
Устойчивость САУ связана с числом пересечений АФЧХ отрезка 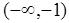 отрицательной вещественной полуоси (Рис.4.7). Когда АФЧХ пересекает эту полуось, ЛФЧХ пересекает одну из линий
отрицательной вещественной полуоси (Рис.4.7). Когда АФЧХ пересекает эту полуось, ЛФЧХ пересекает одну из линий 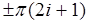 , где
, где 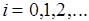 (Рис.4.8).
(Рис.4.8).

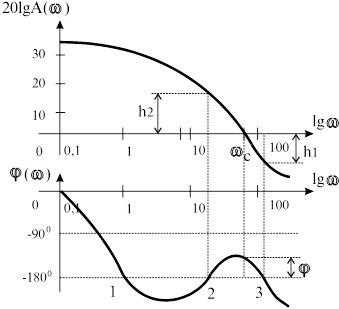
Рис.4.8.
Если пересечения указанных линий происходят справа от точки 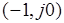 , то они не влияют на устойчивость САУ, если при этом
, то они не влияют на устойчивость САУ, если при этом 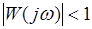 и, следовательно,
и, следовательно, 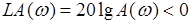 . Поэтому область отрицательных ЛАЧХ при исследовании устойчивости не рассматривается. Интерес представляет только область положительных ЛАЧХ.
. Поэтому область отрицательных ЛАЧХ при исследовании устойчивости не рассматривается. Интерес представляет только область положительных ЛАЧХ.
Сформулируем критерий Найквиста. Для того, чтобы замкнутая САУ была устойчива, необходимо и достаточно, чтобы разность между числом положительных (на Рис.4.8 сверху вниз) и отрицательных переходов (снизу вверх) ЛЧХ прямой 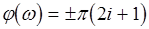 , где i=0,1,2, ... в области
, где i=0,1,2, ... в области 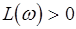 , была равна
, была равна 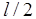 , где
, где 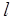 - число правых корней характеристики уравнения разомкнутой САУ.
- число правых корней характеристики уравнения разомкнутой САУ.
Если разомкнутая система устойчива, то и замкнутая система будет устойчивой (Рис.4.7 и 4.8), так как 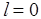 . Запасы устойчивости по амплитуде равны
. Запасы устойчивости по амплитуде равны 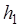 и
и 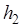 , и по фазе
, и по фазе 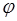 .
.
Дата добавления: 2019-12-09; просмотров: 1048;











