Алгебраических критериев

Алгебраические критерии устойчивости позволяют судить об устойчивости линейных систем по значениям коэффициентов характеристического уравнения

. (1)

Нетрудно показать, что необходимым (но не достаточным) условием устойчивости является положительность всех коэффициентов характеристического уравнения

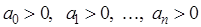. (2)

Заметим, что если все коэффициенты характеристического уравнения отрицательны, то умножив их на -1, получим все положительные коэффициенты.

Если выполняется условие (2), то исследуемая система может быть устойчивой, а может быть и неустойчивой. Однако если условие (2) не выполняется, то система обязательно будет неустойчивой. Докажем это.

Предположим, что все корни характеристического уравнения вещественные. Тогда уравнение (1) можно представить в следующем виде

, (3)

где - корни характеристического уравнения. Будем предполагать, что 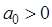. Если это не так, то умножим (1) на -1.

Для устойчивой системы все вещественные корни должны быть отрицательными, поэтому 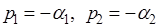и т.д. Тогда (3) примет вид

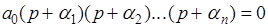. (4)

Раскрыв в (4) скобки, получим уравнение, аналогичное (1) в котором все коэффициенты положительны.

Теперь предположим, что уравнение (1) будет иметь комплексные корни с отрицательными вещественными частями. В этом случае результат не изменится, так как если 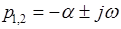, то сомножители в уравнении (3) будут иметь вид

.

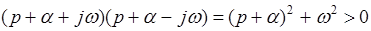Следовательно и в этом случае все коэффициенты в (1) будут больше 0.

Необходимо отметить, что для систем, имеющих характеристическое уравнение первого и второго порядка, необходимое условие устойчивости является и достаточным.

К алгебраическим критериям устойчивости относятся: - критерий, полученный в 1877 г. английским математиком Э. Раусом; - критерий, разработанный в 1895 г. немецким ученым А. Гурвицем; - критерий, предложенный в 1914 г. П. Льенаром и Р. Шипаром. Наиболее удобным с точки зрения использования ЭВМ является критерий устойчивости Гурвица (для систем, имеющих порядок характеристического уравнения 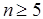его модификацию - критерий Льенара-Шипара), который позволяет по определителям, составленным из коэффициентов характеристического уравнения системы судить об ее устойчивости.

Пусть исследуемая система имеет следующее характеристическое уравнение

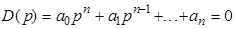. (5)

Из коэффициентов этого уравнения находят главный определитель Гурвица

.

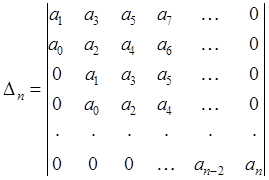По главной диагонали определителя слева направо записываются коэффициенты характеристического уравнения (5), начиная с 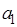по . В столбцы вверх от главной диагонали записываются коэффициенты в порядке возрастания индексов, а в столбцы вниз - коэффициенты в порядке убывания индексов. Если при этом индекс коэффициента становится больше - порядка характеристического уравнения и меньше 0, то данный коэффициент приравнивается 0.

Из главного определителя получают все 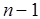определителей Гурвица в следующем виде

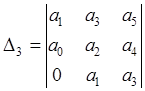и т. д.

Формулировка критерия устойчивости Гурвица такова: для того чтобы система была устойчивой необходимо и достаточно, чтобы при 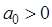были больше нуля все определителей Гурвица.

Необходимо отметить, что -й определитель Гурвица может быть выражен через ( 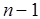)-й следующим образом

.

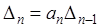Однако в устойчивой системе и должно быть выполнено необходимое условие устойчивости, заключающееся в положительности всех коэффициентов характеристического уравнения, в том числе и 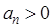, а значит и . Следовательно последний -й определитель в критерии Гурвица можно не находить.

Заметим, что когда все коэффициенты характеристического уравнения положительны и положительны все определители Гурвица с нечетными индексами, то оказываются положительными также все определители Гурвица с четными индексами, и наоборот. Откуда следует формулировка критерия Льенара-Шипара: если все коэффициенты характеристического уравнения положительны, то для устойчивости системы необходимо и достаточно, чтобы среди определителей Гурвица были положительны все определители с четными (нечетными) индексами.