Исследование линейных систем на устойчивость с помощью

Критерия Михайлова

Критерий устойчивости Михайлова относится к частотным критериям в основе которых лежит принцип аргумента, заключающийся в следующем. Известно, что характеристический полином системы

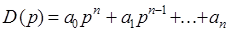(1)

может быть представлен в виде

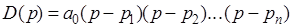, (2)

где 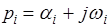- корни характеристического уравнения

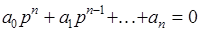. (3)

Рассмотрим 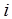-й сомножитель в (2) 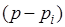и представим его на комплексной плоскости. Корень 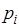может быть изображен в виде вектора, проведенного из начала координат в точку 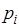, причем длина вектора равна его модулю, то есть 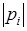, а угол, образованный с положительным направлением действительной оси - аргументу комплексного числа 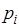, то есть 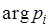(Рис.1).

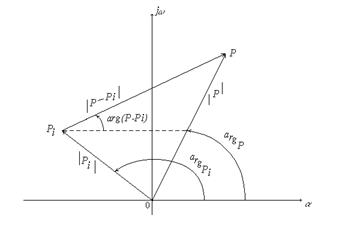
Рис.1.

Аналогично на комплексной плоскости может быть изображен и вектор 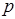, проведенный в произвольную точку этой плоскости. Тогда сомножитель 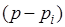представим в виде разности двух рассмотренных векторов. В частном случае при 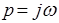, где 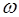представляет собой частоту колебаний, соответствующих мнимому корню характеристического уравнения, характеристический полином примет вид

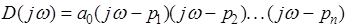. (4)

Тогда концы векторов 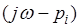будут располагаться на мнимой оси в точке 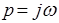(Рис.2).

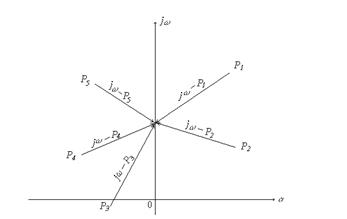
Рис.2.

Необходимо отметить, что в (4) 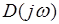представляет собой вектор, модуль которого равен

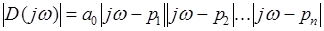, (5)

и аргумент

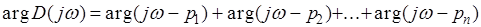. (6)

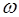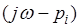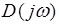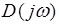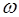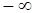При изменении частоты каждый элементарный вектор в (4) будет поворачиваться, изменяя и модуль в соответствии с (5) и фазу (аргумент) в соответствии с (6). Считая поворот вектора против часовой стрелки положительным, при изменении от до 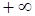каждый элементарный вектор в (4) повернется на угол + 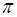, если его начало координат, то есть корень 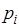, расположено слева от мнимой оси, и на угол - 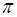, если корень расположен справа от мнимой оси. Такой поворот элементарных векторов 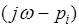и 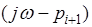изображен на Рис.3.

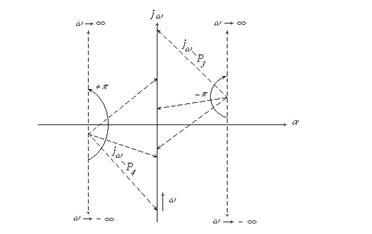
Рис.3.

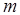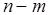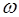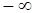Если характеристический полином имеет правых и левых корней, то при изменении от до 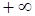вектор 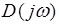повернется на угол, равный сумме поворотов элементарных векторов 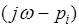, то есть изменение аргумента равно

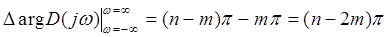. (7)

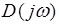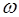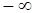Сформулируем принцип аргумента: изменение аргумента при изменении частоты от до 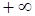равно разности между числом левых и правых корней характеристического уравнения, умноженной на .

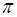При изменении 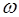от 0 до 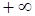изменение аргумента вектора 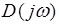будет вдвое меньше

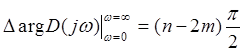. (8)

В 1936 г. на основании принципа аргумента (8) А.В. Михайловым был сформулирован следующий критерий устойчивости: для того чтобы система 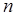- го порядка была устойчива, необходимо и достаточно, чтобы вектор 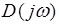, описывающий кривую Михайлова, при изменении частоты 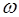от 0 до 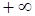повернулся вокруг начала координат против часовой стрелки, нигде не обращаясь в 0 на угол .

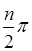Заметим, что кривая (годограф) Михайлова для устойчивых систем всегда должна начинаться на вещественной положительной полуоси, поскольку пр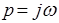и и 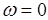из (1) следует, что 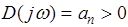на основании необходимого условия устойчивости.

Для построения кривой Михайлова необходимо представить характеристический полином в виде

,

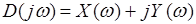где 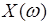- вещественная, а 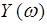- мнимая функции Михайлова и строить кривую Михайлова на комплексной плоскости с осью ординат 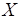и осью абсцисс .

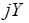Для устойчивых систем кривая Михайлова имеет плавную спиралевидную форму и уходит в бесконечность в том квадранте координатной плоскости, номер которого равен порядку характеристического уравнения. На Рис.4 изображены кривые Михайлова, соответствующие устойчивым системам, а на Рис.5 - кривые неустойчивых систем.

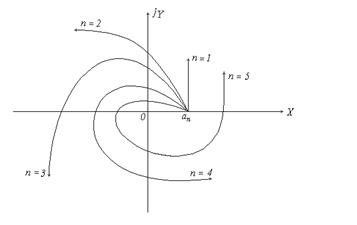
Рис.4.

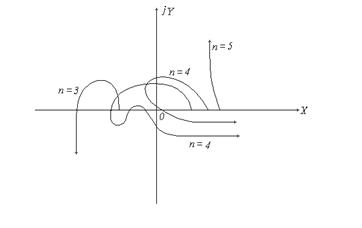
Рис.5.