Построение ЛАЧХ типовых сомножителей передаточных функций.

Анализ передаточных функций типовых звеньев показывает, что их можно представить в общем виде 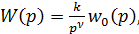где k – статический коэффициент передачи (безынерционное звено); если ν = 0, то звено статического типа, если ν = 1, то звенья астатического типа. В 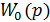входят звенья статического типа, представляемые типовой скобкой (Tp+1), стоящей либо в числителе, либо в знаменателе. Следовательно, необходимо научиться строить ЛАЧХ сомножителя 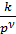и типовой скобки (Tp+1). Рассмотрим подходы к построению.

1) Типовой сомножитель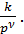

а) Если ν = 0, то этот сомножитель представляет собой безынерционное звено, для которого АЧХ: A(ω)=k, ФЧХ: φ(ω)=0. Следовательно, L(ω)=20 lg k представляет собой прямую, идущую от ω=0, параллельную оси частот.

б) Если ν = 1, АЧХ: 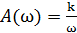, ФЧХ: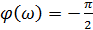

ЛАЧХ: .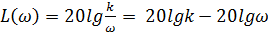

Получили уравнение прямой. Как известно, чтобы провести прямую на плоскости, необходимо иметь либо 2 точки, либо 1 точку и угол наклона. Проведем исследование зависимости L(ω) в пределах одной декады от ω=1 до ω=10.

Пусть ω = 1. Тогда 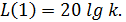Следовательно, на частоте ω=1 мы получили значение ординаты характеристики, т. е. точку, через которую пройдет прямая.

Пусть ω = 10. Тогда 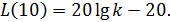Следовательно, за одну декаду значение L(ω) уменьшилось на 20 дБ и можно ввести понятие угла наклона характеристики -20 дБ/дек. Для определения такого наклона всегда можно построить шаблон. Однако можно найти и вторую точку, а именно, частоту, на которой ЛАЧХ пресекает ось частот. В этом случае L(ω)=0. Следовательно

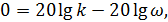
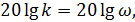
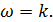
На рис. 20 построены ЛЧХ сомножителя для значения k = 100.

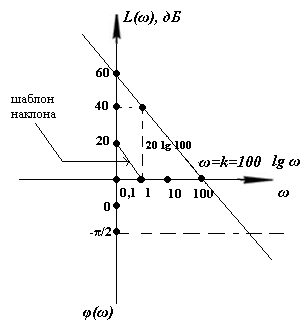
Рис. 20. ЛЧХ сомножителя

2) Типовой сомножитель (Tp+1). Для него АЧХ: 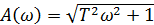, ФЧХ: 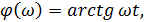ЛАЧХ: 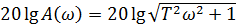. Из выражения следует, что ЛАЧХ имеет нелинейный характер и построение этой характеристики в логарифмическом масштабе неудобно. На практике пользуются асимптотическими ЛАЧХ, заменяя нелинейную зависимость двумя полупрямыми. Рассмотрим возможность такой замены.

Пусть 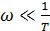. В этом случае слагаемым 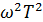под радикалом можно пренебречь и 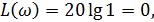т.е. до частоты 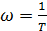, которая называется сопрягающей, ЛАЧХ представляет собой полупрямую, начинающуюся из 0 частот и проходящую по самой оси частот.

Пусть 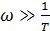. Тогда единицей под радикалом можно пренебречь и 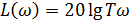. Полученное выражение представляет собой полупрямую, которая начинается на оси частот из сопрягающей частоты 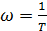и проходит с наклоном +20 дБ/дек. Очевидно, что если бы эта скобка стояла в знаменателе, то после сопрягающей частоты наклон бы поменялся на -20 дБ/дек.

Анализируя полученный результат, можно сделать вывод о том, что сложение ЛАЧХ, например, от безынерционного звена и инерционной скобки выливается в алгебраическое сложение наклонов на сопрягающей частоте. На рис. 21 приведены ЛЧХ инерционного звена с k = 10 и T = 0,1 c, т. е.

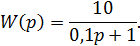
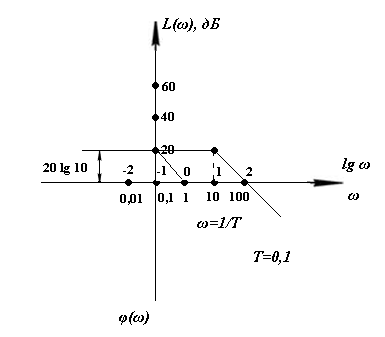
Рис. 21. ЛЧХ инерционного звена

Для него 20lg k = 20 дБ,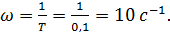

АЧХ, ФЧХ и ЛАЧХ приведены в таблице 4.