Временные характеристики.
Динамические свойства звена могут быть определены по его переходной функции и функции веса.
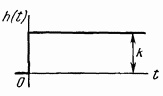
Переходная функция, или переходная характеристика, h(t) описывает переходный процесс на выходе звена, возникающий при подаче на его вход скачкообразного воздействия при величине скачка, равной единице (рис.14).
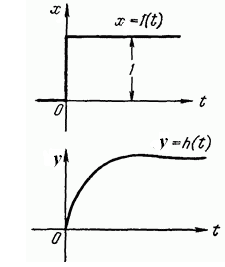
Рис. 14. Переходная характеристика
Такое входное воздействие называется единичной ступенчатой функцией и обозначается 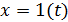 , что соотсветствует
, что соотсветствует 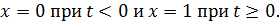 Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена.
Предполагается, что единица имеет ту же размерность, что и физическая величина на входе звена.
Если входное воздействие представляет собой неединичную ступенчатую функцию 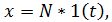 выходная величина будет равна
выходная величина будет равна 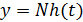 .
.
Умножение какой-либо функции времени x(t) на единичную ступенчатую функцию 1(t) означает, что функция времени x(t) будет существовать только при 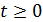 , при
, при 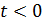 она обращается в нуль. Это показано на рис. 15.
она обращается в нуль. Это показано на рис. 15.
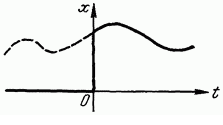
Рис. 15. Область существования функции времени
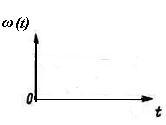
Функция веса 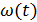 представляет собой реакцию звена на единичную импульсную функцию, поданную на вход (рис. 16).
представляет собой реакцию звена на единичную импульсную функцию, поданную на вход (рис. 16).
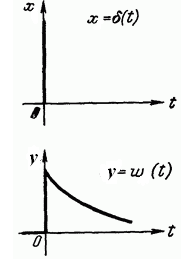
Рис. 16. Функция веса и единичная импульсная функция
Единичная импульсная функция или дельта-функция представляет собой производную от единичной ступенчатой функции: 
Дельта-функция тождественно равна нулю повсюду, кроме точки 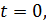 где она стремится к бесконечности. Основное свойство дельта-функции заключается в том, что :
где она стремится к бесконечности. Основное свойство дельта-функции заключается в том, что :
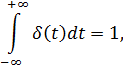
т. е. она имеет единичную площадь.
Из последнего выражения следует, что размерность дельта-функции равна 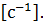
Нетрудно установить связь между переходной функцией и функций веса. Рассмотрим входное воздействие звена в виде конечного по высоте и ширине импульса с площадью 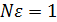 , прикладываемого при
, прикладываемого при 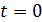 (рис.17).
(рис.17).
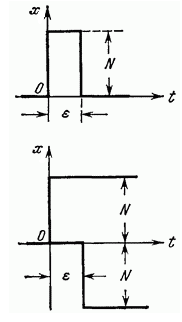
Рис. 17. Входное воздействие звена в виде импульса
Такой импульс может быть заменен двумя ступенчатыми функциями 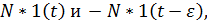 прикладываемыми ко входу звена со сдвигом во времени ε. Тогда выходная величина будет равна:
прикладываемыми ко входу звена со сдвигом во времени ε. Тогда выходная величина будет равна:
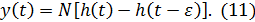
Будем теперь увеличивать высоту импульса N,одновременно уменьшая его ширину ε, но так, чтобы все время площадь импульса равнялась единице, т. е. 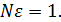 Помножив и поделив правую часть равенства (11) на ε и перейдя к пределу, получим функцию веса:
Помножив и поделив правую часть равенства (11) на ε и перейдя к пределу, получим функцию веса:
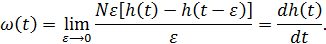
Таким образом, функция веса может быть получена дифференцированием по времени переходной функции.
Переходная функция и функция веса связаны с передаточной функцией звена соотношениями:
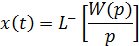

Следовательно:
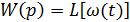
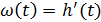
Переходные характеристики можно получить экспериментально или в аналитическом виде, используя различные методы, включающие как непосредственное решение дифференциального уравнения с нулевыми начальными условиями, использование обратного преобразования Лапласа и теорем, так и получая переходные характеристики основных простых звеньев и представляя более сложные как сумму элементарных переходных характеристик. Покажем на примерах.
1) Безынерционное звено 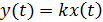 , где
, где 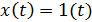 . Очевидно, что
. Очевидно, что 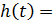
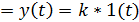 .
.
2) Идеальный интегратор 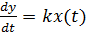 , где
, где 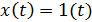 . Очевидно, что выходная величина, которая представляет собой переходную характеристику – интеграл от правой части уравнения
. Очевидно, что выходная величина, которая представляет собой переходную характеристику – интеграл от правой части уравнения 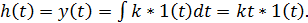
3) Идеальный дифференциатор 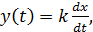 где
где 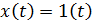 , а
, а 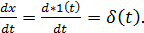
Следовательно, 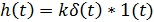 .
.
4) Инерционное звено 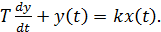 Найдем переходную характеристику непосредственным решением дифференциального уравнения. Характеристическое уравнение имеет вид:
Найдем переходную характеристику непосредственным решением дифференциального уравнения. Характеристическое уравнение имеет вид:
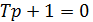
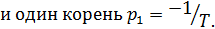
Общий вид решения:
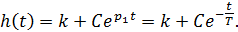
При нулевых начальных условиях
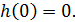
Следовательно 0 = k + c и c = -k. Окончательно получим:
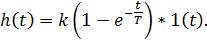
Дифференцируя это выражение, получим весовую функцию:
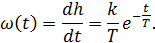
Все переходные характеристики остальных звеньев легко получить, если разложить их на сумму элементарных звеньев с учетом инерционного. Суммарная  равняется алгебраической сумме переходных характеристик. Например, для изодромного звена, соединяя параллельно идеальный интегратор
равняется алгебраической сумме переходных характеристик. Например, для изодромного звена, соединяя параллельно идеальный интегратор  и безынерционное звено
и безынерционное звено 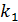 по правилу эквивалентных передаточных функций параллельных соединений, получим:
по правилу эквивалентных передаточных функций параллельных соединений, получим:
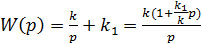 , где
, где 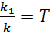 .
.
Следовательно, переходная характеристик есть сумма характеристик безынерционного звена с коэффициентом передачи k1 и интегрирующего с коэффициентом передачи k. По аналогии, форсирующее звено k(Tp+1) есть сумма элементарных звеньев kTp и k, т. е. представляет собой сумму переходных характеристик идеального дифференциатора и безынерционного звена. При разложении на простые звенья более сложных, например интегратора с замедлением для представления его в виде суммы идеального интегратора и инерционного звена, необходимо воспользоваться правилом разложения на дроби с неопределенными коэффициентами. Передаточные функции, переходные и весовые характеристики типовых звеньев приведены в таблице 3.
| Тип звена и его передаточная функция | Переходная функция h(t) | Функция веса ω(t) |
Безынерционное
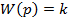
| 
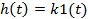
| 
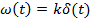
|
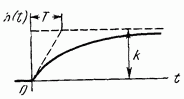
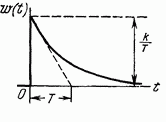
Апериодическое 1-го порядка
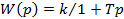
| 
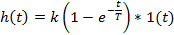
| 
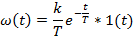
|
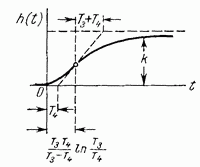
Апериодическое 2-го порядка
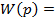
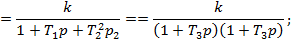
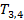 = = 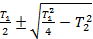 (
( 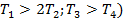
| 
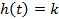 (1− (1− 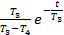 +
+ +
+ 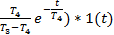
| 
 ) ) 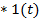
|
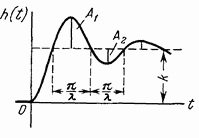
Колебательное
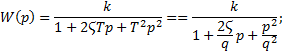
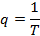
| 
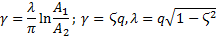
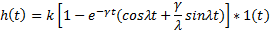
| 
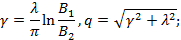
 = = 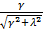 ; ;
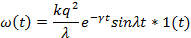
|
Таблица 3. Временные характеристики звеньев автоматики
Таблица 3. (Продолжение)
| Тип звена и его передаточная функция | Переходная функция h(t) | Функция веса ω(t) |
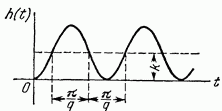
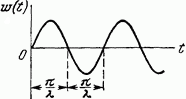
Консервативное
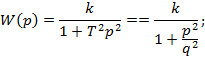
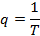
| 
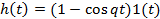
| 
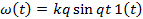
|
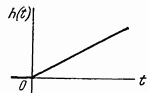
Идеальное интегрирующее
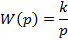
| 
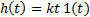
| 
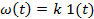
|
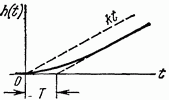
Интегрирующее с замедлением
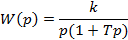
| 
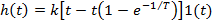
| 
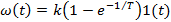
|
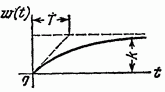
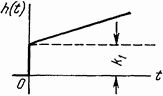
Изодромное
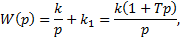
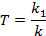
| 
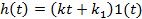
| 

|
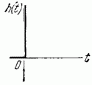
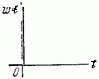
Идеальное дифференцирующее
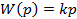
| 
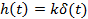
| 
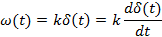
|
Таблица 3. (Окончание)
| Тип звена и его передаточная функция | Переходная функция h(t) | Функция веса ω(t) |
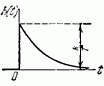
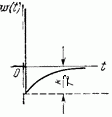
Дифференцирующее с замедлением
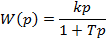
| 
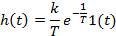
| 
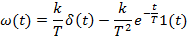
|
Форсирующее
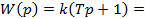
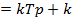
| 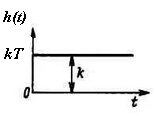
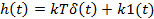
| 
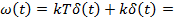
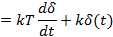
|
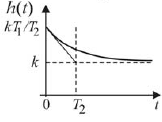
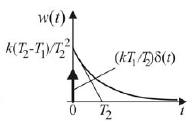
Инерционно-форсирующее звено
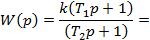
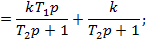
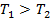
| 
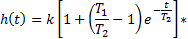
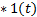
| 
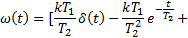
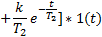
|
Дата добавления: 2022-02-05; просмотров: 728;











